Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— 304 —

новая мысль, жадно впитывающая все, что было создано на Востоке, и перерабатывающая все это древнейшее наследие.

Однако все же на территории Вавилона, несмотря на смены народов, научные труды и интересы сохраняются еще долгое время. Греческая культура была основана на труде рабов, которых приводили в страну в качестве военнопленных греческие воины. Тем не менее эта новая цивилизация создала нового любознательного человека, которого интересовали многие вопросы, особенно астрономия, а за ней математика, которая развивалась рядом с учением о правильном размышлении — логикой.

— Ну, разбираешься ли ты в том, что слышишь? — спросил Радикс.

— Кажется, разбираюсь. А если я в чем-нибудь запутаюсь, я потом спрошу тебя.

— Надо помнить, что новый мир Древней Греции, — взял слово Радикс, — породил людей, которые благодаря своему приволью и богатству занимались наукой не только по необходимости хозяйственной, а независимо от этого, ради желания проникнуть в суть научного рассуждения, в существо решения трудных задач. А затем греческие ученые постепенно стали переходить и к новым задачам, которых древневосточный мир либо не ставил, либо не придавал им особого значения.

— Вот мы вспоминали об удвоении площади, — добавил Коникос, — тут нужен корень из двух. В этом случае всего проще взять самое грубое приближение, то есть дробь 7/5, которая иначе 1,4, то есть корень из двух с точностью до первого десятичного знака. Если 7/5 возвести в квадрат, получается 49/25, или 1,96, то есть двойка с ошибкой на четыре сотых. Для плотника это отлично. Но греки на этом не хотели останавливаться и стали изучать теорему Пифагора (которую прекрасно знали и на Востоке) и вскоре открыли, что вся трудность не в вычислении, а в том, что корень из двух совсем необычное число, которое очень легко построить геометрически…

— А как его построить? — еще раз спросил Радикс, обращаясь к Илюше.

— Так это будет диагональ единичного квадрата, о котором мы только что говорили! — не задумываясь воскликнул Илья и посмотрел на Радикса.

— Молодец! — похвалил Асимптотос. — Признаться, не ожидал от тебя такой прыти!

— … очень легко построить, — продолжал Коникос, — но невозможно точно вычислить. Вот тогда открыли иррацио-

— 305 —

нальные числа, а затем придумали особенное построение, при помощи которого эту величину можно вычислить с любой степенью точности [23] Это построение называется диагональными числами. Об этом можно прочесть в АЛ-II, XV, 1, 2, 3; XXII, 5. Ныне все это связано с цепными дробями, о которых говорится в АЛ-II, XXII, ХХIII. Этими дробями занимался в XVI веке Рафаэль Бомбелли. Мы с ним еще встретимся. . Одно открытие привело к другому.

— Значит, это было замечательное открытие!

— Конечно! Наука стала объяснять законы счета, проникать во все своеобразие этих законов. Халдей говорил: «Делай так, потому что иначе ничего не выйдет!» А грек говорил:

«Рассудок учит, что, делая вот так, ты следуешь законам мира чисел, а поступая иначе, ты эти законы безрассудно нарушаешь, поэтому-то ты в последнем случае и расплачиваешься ошибкой!»

— Но ведь халдей даже не знал об этих законах? — спросил Илюша.

— Действительно, не знал, вернее, не догадывался. Да ведь и греки не сразу догадались…

— Но зачем же древневосточным ученым нужен был корень квадратный из двух с такой точностью, которая на практике была им не нужна? — спросил Илюша.

— Прямо ответить на этот вопрос невозможно, — сказал Коникос, — но уж раз мы знаем, что такие весьма точные вычисления существовали, мы убеждаемся в том, что либо это делалось просто из научной любознательности, либо это были упражнения для учеников. Но и в том и другом случае это все-таки очень похоже на то, что мы теперь называем наукой. Возможно, что некоторые вопросы, вроде теории квадратного уравнения, изучались преимущественно на числовых решениях. Может быть, это не самый лучший способ анализа, но и он давал некоторые результаты. Квадратное уравнение вавилоняне решали просто: находили два числа по их сумме и произведению… Что ты на это скажешь?

— На основании формул Виета как раз выходит квадратное уравнение:

х 2+ рх + q = 0.

Сумма его корней равна р с обратным знаком, а их произведение = q .

— Вавилонянин решал задачу так: либо эти искомые величины (корни) равны между собой, либо нет. Если нет, то между ними есть некая разность z . Тогда можно написать, что

x 1= - p /2 + z ; x 2= — p /2 — z , где z = 1/2( x 1— x 2).

— 306 —

Затем во второе уравнение x 1 · x 2= q подставляем эти значения корней и приходим к известной формуле квадратного уравнения, что нетрудно проверить.

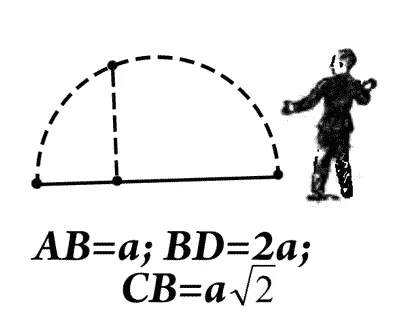
AB = a ; BD = 2 a ; CB = a √2

Илюша немного повозился с расчетами, выяснил, что получается, а затем сказал:

— Но ведь ученый халдеи не знал формул Виета?

— Формул, конечно, он не знал, но самый факт определенных взаимоотношений между исходными данными такой задачи и ее решением не мог быть для него тайной, потому что тогда он не сумел бы так решить задачу. Формулировать это еще не умели и не понимали, может быть, сколь это полезно, но факт был известен. Догадываешься, в чем тут разница?

— Как будто… то есть, как вы говорите, не знали, почему?

— Вот именно, — подтвердил Радикс. — Удвоить квадрат оказалось довольно просто, а основное правило решения выясняется при помощи теоремы Пифагора. Если сторона квадрата равна а , то мы узнаем хиз пропорции:

Ты, наверно, помнишь, как геометрически производится построение средней пропорциональной?

— Конечно! — отвечал мальчик. — Это мы по геометрии проходили. Откладываешь на прямой отрезки, равные а и 2 а , и на их сумме, то есть на 3 а , строишь полуокружность, радиус которой равен 1,5 а . А теперь, если АВ будет отрезок а и 2 а отрезок BD , то из точки В ты восстанавливаешь перпендикуляр до пересечения с окружностью — это и будет искомая средняя пропорциональная. Доказать, что это так, нетрудно. Теорема Пифагора все тут объясняет.

— Хорошо. Таким образом, тебе, следовательно, ясно, что, применяя это несложное построение, для которого ты пользуешься двумя известными тебе по своим свойствам геометрическими местами, то есть прямой и окружностью — иначе сказать, линейкой и циркулем, — ты получишь совершенно точно искомую величину. Но затем стал вопрос об удвоении объема. Тут нужен не квадратный, а кубический корень из двух. Конечно, и для него не так уж трудно найти грубое приближение, вроде дроби 29/23, потому что, если эту дробь возвести в куб, получится 24389/12167 что равно 2,0045, то есть двойка с ошибкой