Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— 301 —

образом, из дошедших до нас документов — преимущественно обожженных глиняных плиток-таблеток, на которых перед обжигом наносились знаки, — большинство относится к развитой государственной жизни, когда необходимо учитывать урожай, сбор шерсти, рассчитать, как построить плотину, мост, сколько потребуется народу, чтобы возвести то или иное сооружение, и так далее. Многие таблички представляли собой учебники для школ будущих чиновников, которые и должны были уметь делать все эти вычисления. Составлялись таблицы для облегчения расчетов. Важное значение имела и астрономия, в основном как служба календаря, определявшая сроки сельскохозяйственных работ.

— А как все это узнали? — спросил Илья.

— Глиняные таблетки, — продолжал Коникос, — которые находят археологи при раскопках, — материал прочный, под землей могут пролежать тысячи лет, огня не боятся. В восточных царствах было накоплено, по-видимому, много практических знаний. Существовала ли в то время теоретическая математика, сказать трудно, но что какие-то начатки теории уже были, в этом, по-видимому, нельзя сомневаться. Среди Вавилонских таблеток можно встретить чертежи правильных многоугольников, причем вычисляются их площади, встречаются приближенные определения квадратного корня из двух, находится приближенная квадратура круга, существуют способы определения довольно сложных объемов, решаются квадратные уравнения и многое другое. Трудно сказать, осмыслено ли все это было теоретически. Но все же приходишь к мысли, что кое-что делалось… Никакой хозяйственной необходимости, например, вычислять площадь круга в то время не было. Однако в учебниках есть задачи на вычисление: сколько семян надо, чтобы засеять круглое поле? Хотя круглых полей делать никто не станет. Греческие философы передают, что в египетских храмах в течение тысячелетий хранились записи всего нужного и интересного. Там имелись и астрономические наблюдения, и очень трудно допустить, чтобы при всем этом можно было бы обойтись совсем без научных работ. Практика больших сооружений в странах с искусственным орошением и с постоянными работами по усмирению больших рек могла поставить трудные задачи.

— Интересны эти задачи на вычисление насчет круглого поля! — заметил Илюша.

— Конечно, интересно! — откликнулся Асимптотос. — Крупные ученые-историки приходят к заключению, что у вавилонян неизбежно должно было возникнуть что-то вроде нашего доказательства, когда сложное решение вопроса опирается на целую цепь более простых соображений. Конечно, вряд ли им

— 302 —

приходило в голову интересоваться, как достигается тот или иной теоретический вывод, но им уже нельзя было обойтись без того, чтобы не пользоваться им.

— Когда все это было?

— У шумеров, — отвечал Коникос, — примерно в третьем тысячелетии до нашей эры, но там о теории, наверно, еще и слуху не было, а во втором и первом тысячелетиях до нашей эры процветал Вавилон, особенно в первой половине первого тысячелетия до нашей эры. Древняя Греция оказалась наследницей всего этого научного богатства.

— А как бы в общем сказать про эту древневосточную науку? — задумался Илюша.

— Пожалуй, — заметил Асимптотос, — верней всего было бы сказать, что это была наука писцов, чиновников, казенных канцелярий. Постепенно там родился интерес и к самому искусству вычисления, а из него мало-помалу выросла и алгебра в виде первых решений квадратных уравнений. Причем пока еще никто не мог найти ни одной практической задачи на Древнем Востоке, для которой было бы необходимо решение квадратного уравнения. Поэтому историки и считают, что это решение искали не для практики, а именно из чисто научного интереса. Наука Вавилона, видимо, была выше египетской. Одним из замечательных достижений шумеро-вавилонских ученых было построение позиционной системы счисления. Она, правда, была не такая, как наша общепринятая десятеричная, а была шестидесятеричная. Она еще и у нас осталась в делении окружности на триста шестьдесят градусов, час мы делим на шестьдесят минут, а минуту на шестьдесят секунд.

— Какая живучая система! — усмехнулся Радикс.

— Историки считают, — продолжал Коникос, — что изобретение позиционной, или поместной, системы настолько важно было для культурного развития человека, что это можно вполне сравнить с изобретением письменности. Вавилоняне знали теорему Пифагора — и не только для отдельных случаев, по и вообще. На одной вавилонской таблетке дано численное значение корня квадратного из двух, правильное до шестого десятичного знака [22] Снимок этой таблетки есть в книге Ван дер Вардена «Пробуждающаяся наука», которую мы уже вспоминали. А таблетке этой примерно три или четыре тысячи лет. . Конечно, корень из двух, позволяющий увеличивать данную площадь вдвое, необходим в строительном деле. Но с такой точностью он ни одному столяру или каменотесу совсем не требуется. В деле строительства вполне можно было бы удовлетвориться двумя знаками, а впрочем, можно даже взять расчеты и погрубее.

— 303 —

— А помнишь ли ты, — спросил Радикс мальчика, — как с помощью корня из двух удваивается данная площадь?

— Еще бы! Если дан квадрат, а сторона равна единице, то диагональ по теореме Пифагора будет равна корню из двух. Вот и удвоение площади! Умножил сторону на этот корень и получил сторону квадрата с двойной площадью.

— Хорошо! Знаешь твердо. Учись, не отставай, и все будет в порядке. А мы всегда к твоим услугам.

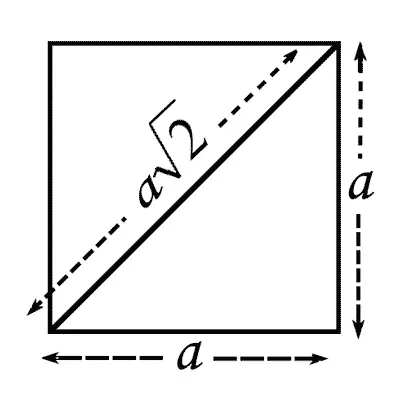
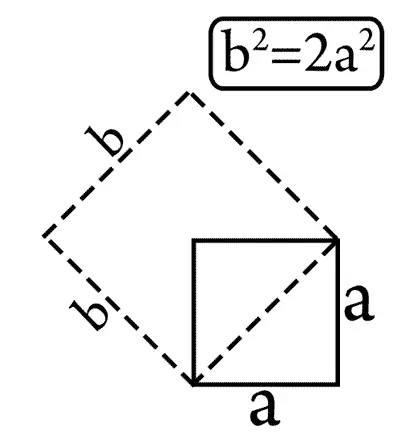
Площадь квадрата, построенного на диагонали другого, вдвое больше площади последнего.

— Вот что еще мы можем рассказать тебе о Древнем Востоке, — добавил Коникос. — Примерно в начале первого тысячелетия нашей эры вокруг Средиземного моря происходят огромные перемены. К морским берегам из глубины континентов приходят новые люди. Бронзовые мечи и топоры заменяются железными, гораздо более удобными и дешевыми. Несколько столетий подряд на берегах Средиземного моря и его островах бушуют непрерывные битвы. Падает под ударами врага мощное Критское царство, которое было тоже центром культуры бронзового века. Впрочем, теперь археологи склоняются к мысли, что Критская островная культура могла погибнуть почтя внезапно из-за грандиозного извержения вулкана неподалеку, страшного землетрясения и всеразрушающих морских волн, которые называются цунами (они достигают огромной высоты и все уничтожают на своем пути, неожиданно обрушиваясь на сушу, а потом с той же силой стекая обратно в море). А затем под натиском «людей с моря» слабеет Египет. В Греции начинается новая культура, появляются мореплаватели, купцы, градостроители — люди, пользующиеся большой свободой по сравнению с вавилонянами и египтянами. Греческий город, а не дворец деспота становится хозяином нового мира. Восток пробует подчинить новую культуру — персидские полчища идут на греков и терпят неудачу. И вот в этом мире, где наука освободилась от религии, расцветает