Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— А что же тут такого? — спросил Илюша. — Не понимаю, почему нельзя рассуждать об изменении явлений, исходя из простой пропорциональности, если это всякому понятно?

— Дело не в том, что нам «понятно», — продолжал Радикс, — и какого мы «мнения» о явлениях, а в том, каковы законы этих явлений! А ведь они существуют сами по себе, мы можем только изучать их, но не навязывать явлениям наши «мнения». Мне достаточно того, что я устанавливаю, что в природе имеются не только зависимости пропорционального характера. Хорошо, если ты можешь сразу ответить на вопрос «почему?». А ведь есть немало случаев, когда это не так легко сделать. Например, на лодке установлен моторчик в 1,25 лошадиной силы, и лодка идет со скоростью восемь километров в час. Можно ли утверждать, что если я поставлю на эту лодку мотор в десять сил, то лодка помчится, как скорый поезд, и будет делать шестьдесят четыре километра в час? Нет, этого утверждать нельзя. Чтобы увеличить скорость в n раз, надо мощность увеличить примерно в n 3раз, а чтобы достичь такой скорости, придется обзавестись мотором не в десять, а в шестьсот сорок сил, тогда как десятисильный мотор даст только удвоенную скорость. Еще пример: ты без всякого труда можешь закинуть спортивный диск весом в восемьсот граммов на восемнадцать шагов. Но можно ли из этого вывести, что более легкий диск, в двадцать граммов весом, ты закинешь со-

— 339 —

гласно тройному правилу на семьсот двадцать шагов, то есть без малого на полкилометра? Разумеется, это сплошная ахинея, ибо такой очень легкий предмет далеко не забросишь, а уж о полкилометре смешно и говорить даже. Нередко исследователь вовсе и не задается вопросом «почему?». Очень хорошо, если он может ответить на вопрос «как?». Мы не знаем, что такое тяготение, но отлично знаем, как оно действует, и поэтому можем вычислить и траекторию артиллерийского снаряда, и толщину фундамента для большого здания, и многое другое. На этот вопрос Галилей дал совершенно точный ответ для случая падения тел. Надо еще принять во внимание то, что открытия Кеплера и Галилея связали воедино механику с геометрией, то есть как раз такие две науки, которые греки как бы противопоставляли одну другой. А вскоре выяснилось, что метод касательных имеет непосредственное отношение к бесконечно малым.

— Вот как! — сказал Илюша. — Как же это получилось?

— Дело вот в чем, — отвечал Радикс. — Давай-ка нарисуем кривую и проведем секущую. Она пересечет кривую на чертеже два раза — в точках А и Б . Дальше мы будем рассуждать так. Наша кривая связывает две величины — х и у . Их мы будем называть переменными: икс — независимой переменной, а игрек — зависимой. Ведь действительно, вспомни, как мы подставляли в уравнения различные произвольные значения икса и следили за изменением игрека. Значит, в самом деле игрек изменяется в зависимости от икса. Или, как принято говорить, игрек есть функция икса.

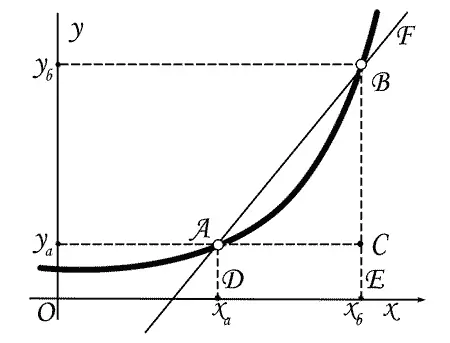
Если заставить точку В двигаться по кривой АВ к точке А , то секущая ABF , поворачиваясь около точки А , будет приближаться к некоторому предельному положению, когда бесконечно малое расстояние между точками А и С обратится в нуль; в этот миг секущая превратится в касательную.

Теперь заметим, что в точке А икс равен, допустим, некоторой величине х а , а игрек соответственно равен у a . Теперь увеличим немного икс, то есть дадим ему некоторое приращение. Тогда икс, соответственный точке В , будет равен х b , а игрек соответственно у b . Приращение икса будет равно x b — x a ; приращение игрека y b — y а — Проведем теперь секущую через точки

— 340 —

А и В . Если теперь поворачивать секущую около точки А по часовой стрелке, то в пределе она станет касательной. Построим треугольник ABC и рассмотрим, что с ним будет делаться, если поворачивать секущую около точки В . Очевидно, стороны треугольника убывают.

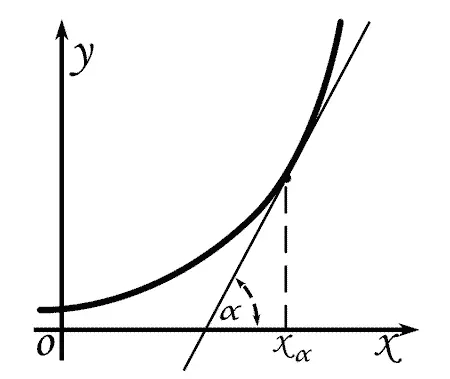
tg α называется производной «ординаты кривой по абсциссе» в точке с абсциссой x a

Уменьшается сторона АС , а вместе с ней и сторона ВС , то есть уменьшается приращение той и другой переменных и уменьшается непрерывно. В рассматриваемых здесь случаях отношение АС и ВС стремится к некоторому пределу, а секущая занимает свое предельное положение относительно кривой, то есть становится касательной. Когда АС бесконечно уменьшается, то и ВС уменьшается таким же образом. Обе эти переменные бесконечно уменьшающиеся приращения величин суть бесконечно малые, и нам тут необходимо найти предел, к которому стремится их отношение. Очевидно, что оно будет равно тангенсу угла, который образует касательная с положительным направлением оси абсцисс. Этим вопросом занимается дифференциальное исчисление; и тангенс наклона касательной к положительному направлению оси абсцисс называется производной данной функции. Зная производную той или иной функции, узнают, с какой скоростью изменяются ординаты кривой при изменении абсцисс, и можно изучить эту скорость. А этим способом исследуют очень- многие законы физики, механики и других естественных наук. На этом фундаменте и выросла наша современная техника.

— Это замечательно! — воскликнул Илюша. — Только я не пойму: к какой кривой приводит тот или иной закон физики?

— Видишь ли, когда этим занялся Исаак Ньютон, которого современники называли «счастливейшим из смертных» за его открытие закона всемирного тяготения, то он, изучая скорость, с которой изменяются ординаты данной кривой, поставил два чрезвычайно важных и вполне естественных вопроса. Он рассуждал так: если точка двигается с данной скоростью, это значит, что она в определенное время проходит некоторый путь. Будем называть икс временем, как это делал сам Ньютон. Тогда ординаты кривой дают нам пройденный путь. Вот, например, если поезд идет с постоянной скоростью сорок

— 341 —

километров в час, то за десять часов он пройдет 10 · 40 = 400 километров. Алгебраически это будет: скорость равна а , время равно х , пройденный путь у равен ах . Таким образом, уравнение пути будет у = ах . Это есть не что иное, как уравнение прямой линии. Если же скорость сама все время меняется пропорционально времени, то пройденный путь будет на чертеже изображаться не ординатой прямой, а ординатой параболы. Если же мы умеем построить к нашей кривой пройденного пути касательную, то тем самым можем определить скорость в каждой данной точке кривой или в любой момент времени. Таким образом, зная пройденный путь, мы находим скорость. Но можно поставить и обратную задачу; зная скорость, найти пройденный путь. Можно показать, что эта задача сводится к квадратуре кривой, то есть к определению ее площади, а это, как уже мы с тобой говорили, есть задача интегрирования. Так вот, таким путем Ньютон и выяснил, что нахождение касательной и определение площади суть действия, обратные друг другу, как обратны, например, возведение в степень и извлечение корня.