Рене Декарт - Рассуждения о методе. Начала философии. Страсти души (сборник)

LVIII. Чтобы яснее увидеть это, сравним движенье, которым камень, находясь в А, несется к С, если тому не препятствует иная сила, с движением муравья, находящегося в той же точке А и направляющегося к С, если линия ЕV [31] Рисунок тот же. Буква V означает предельную точку в движении по прямым ED, EC, EG, а X – промежуточное положение на тех же прямых. – Прим. перев. будет палкой, по которой он прямиком идет от А к V, в то время как сама палка вращается вокруг Е и точка А описывает круг ABF; пусть эти два движения так согласованы между собой, что муравей доходит до X, когда палка будет в С, и до V, когда она в G, а муравей все находится на прямой ACG. Затем сравним и ту силу, которой наш камень несется в праще по круговой линии ABF, стремясь удалиться от центра Е по прямым АD, ВС, FG, со стремлением, остающимся у муравья, если перевязью или клеем он будет удержан в точке ЕV; когда эта палка вращается около центра Е по круговой линии ABF, муравей всеми силами стремится идти к V и удаляться от центра Е по прямым ЕАV, ЕВV и т. д.

LIX. Правда, я знаю, что вначале движение этого муравья будет медлительным, что его стремление начать движение не может быть значительно; однако оно не равно нулю и увеличивается с увеличением его результатов, так что развивающееся отсюда движение может приобрести достаточную скорость. Так, приведу другой пример: положим, что ЕV канал, в котором находится шарик А; хотя в первый момент, пока этот канал движется по кругу около Е, шарик будет передвигаться к V медленно, однако в следующий момент он станет передвигаться скорей: он удержит первоначальную силу и сверх того получит свежую от нового стремления удаляться от центра Е. Поэтому чем больше длится круговое движение, тем длительнее становится и это стремление, как бы обновляясь в отдельные моменты. В этом убеждает опыт; если канал ЕV быстро вращается около центра Е, то шарик, находящийся в нем, быстро перейдет от А к V. То же мы видим и в праще; чем быстрее вращается в ней камень, тем больше напрягается веревка, и это напряжение, которое возникает только благодаря силе камня, стремящегося удалиться от центра своего движения, обозначает для нас количество этой силы.

LX. Что сказано здесь о камне в праще или о шарике в канале, вращающемся около центра Е, легко понять в подобном же смысле и относительно всех шариков второго элемента, а именно: каждый из них начинает с достаточно большой силой удаляться от центральной точки вихря, в котором вращается; удерживается же там он другими окружающими шариками лишь так, как камень удерживается пращей. Но эта сила в остальных шариках значительно увеличивается оттого, что верхние и нижние из них все вместе сжимаются материей первого элемента, собравшейся в центре данного вихря. Прежде всего, чтобы все тщательно различать, мы должны повести речь об этих шариках;

а относительно материи первого элемента заметим только, что все занимаемые ею пространства как бы пусты, то есть заполнены материей, которая ни способствует, ни препятствует движению других тел. Истинная идея пустого пространства не может быть иной, как явствует из предыдущего.

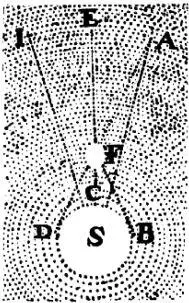
Рис. 9

LXI. Так как все шарики, вращающиеся около S в вихре АЕI, пытаются удаляться от S, как указано, то достаточно ясно, что те, которые расположены на прямой ЕА, все должны взаимно отталкиваться к А, а те, которые расположены на прямой SЕ, должны отталкиваться к Е; то же происходит и с остальными. Поэтому когда их недостаточно, чтобы заполнить все пространство между S и окружностью АЕI, то около S остается незаполненное пространство. И так как те шарики, которые взаимно теснятся (как, например, на линии ES), не все вращаются как палка, но одни быстрее, а другие медленнее совершают свой пробег, как будет позднее отмечено, то оставленное при S пространство не может быть круглым. Если мы вообразим, что многие шарики вначале были на прямой SЕ, а не на SА или SI, так что нижние из них на прямой SЕ были ближе к центру, чем нижние из шариков на прямой SI, то те нижние должны выполнять свой пробег быстрее расположенных на той же линии верхних и ни одни из тех не приобретут быстроты шариков линии SI, как более удаленные от S. Поэтому все нижние шарики этих линий равно удалены от S и оставленное ими пространство BCD должно быть круглым.

LXII. Сверх того нужно заметить, что не только шарики на прямой SE совместно теснятся к Е, но что каждый по отдельности теснится всеми другими, расположенными между прямыми, проведенными от данного шарика к окружности BCD и касающимися ее. Так, например, шарик F теснится всеми, расположенными между линиями BF и DF, то есть на пространстве треугольника BFD, но не столь теснится прочими шариками: если бы место F было пустым, то одновременно все шарики, заключенные в пространстве BFD, а никак не другие шарики, поспешили бы сколь возможно быстрее занять его. Ведь мы видим ту силу тяжести, которая направляет в свободном воздухе падающий камень к центру Земли; не одинаково влечет его туда, когда прямому направлению камня препятствует какая-либо неровная поверхность. Несомненно, что той силы, которой шарики пространства BDF начинают удаляться от центра S, по прямой, ведущей от этого центра, достаточно, чтобы удалить от последнего данный шарик.

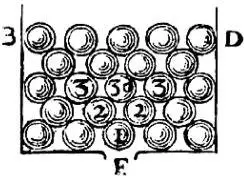
Рис. 10

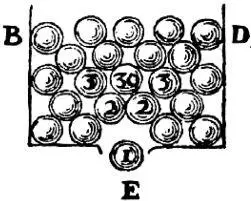
Рис. 11

LXIII. Этот пример с силой тяжести уяснит дело, когда мы рассмотрим следующее: в сосуде BFD (рис. 10) содержатся дробинки и так лежат одна на другой, что когда на дне сосуда проделывается отверстие, то дробинка 1 выпадает в него силой собственной тяжести (рис. 11), за ней следуют две другие 2 и 2, а за ними – 3, 30, 3, и так прочие; таким образом, в тот момент, как нижняя 1 начинает двигаться, все остальные, заключенные в пространстве треугольника BED, вместе опускаются при неподвижности прочих дробинок. Тут должно заметить, что два шарика 2, 2, следуя за упавшей дробинкой 1, разумеется, должны сколь возможно мешать друг другу; но это не имеет места относительно шариков второго элемента, так как они находятся в постоянном движении. Будь они так расположены, как дробинки, то это длилось бы только мгновение и непрерывность их движения не нарушалась бы. Сверх того должно заметить, что сила света состоит не в продолжительном движении, а только в стесненности (pressione) или в первом приготовлении к движению, хотя бы отсюда и не следовало самого движения.

LXIV. Отсюда уясняется, каким образом та деятельность, которую я рассматриваю как свет, распространяется Солнцем или телом любой неподвижной звезды равномерно во все стороны; и в малейший момент времени проходится какое угодно расстояние; поэтому свет проходит по прямой линии не только от центра светящегося тела, но и от любой иной точки его поверхности. Отсюда могут быть выведены все прочие свойства света. Может быть, многим это покажется парадоксом, но все это имелось бы в небесной материи, не будь даже силы в Солнце или иной звезде, около которой материя вращается: таким образом, если бы солнечное тело было не что иное, как пустое пространство, но тем не менее свет, разве только более слабый, в остальном различался бы нами так же, как и теперь по крайней мере в кругу, по которому движется небесная материя; ведь и теперь мы рассматриваем не все направления сферы. И чтобы получить возможность уяснения того, что имеется в самом Солнце и звездах, как увеличивается эта сила света и распространяется по всем направлениям сферы, созданы некоторые предположения о небесном движении.