Карл Зигмунд - Точное мышление в безумные времена. Венский кружок и крестовый поход за основаниями науки

В документах отца Карл Менгер обнаружил неоспоримые доказательства, что памфлет и правда был написан эрцгерцогом и его наставником. Карл написал о своей находке газетную статью и отправил документы в запечатанном конверте в Академию наук в Вене.

Кроме того, отец завещал Карлу множество заметок к запланированному переизданию «Основ национальной экономики», над которым работал после того, как ушел на покой. Предисловие было написано целых тридцать лет назад. Теперь задача подготовить новое издание легла на плечи сына.

«Дело ужасно обременительное и хлопотное, — писал юный Карл в дневнике, — и утешает лишь знание, что я завершил великий труд, важный не только для науки, но, вероятно, и для всего человечества» [301] 301 Дневник Карла Менгера, см. Beham, 2013. . Кроме того, он написал статью в главную австрийскую газету Neue Freie Presse , где объяснял, как восстановить разоренную экономику истерзанного австрийского государства. Газетный редактор приписал: «Мы публикуем статью сына мастера национальной экономики, хотя не согласны ни с одним его выводом» [302] 302 Neue Freie Presse, 17 ноября 1921. .

Юный Менгер разнес в пух и прах налогово-бюджетную политику Вильгельма Розенберга, занимавшего руководящий пост в правительстве, поскольку считал, что она привела к гиперинфляции; Розенберг пригласил девятнадцатилетнего юношу на обед. За едой Розенберг объяснил, что наладить послевоенную экономику Австрии не так просто, как, видимо, думает Менгер. Даже прославленный экономист Йозеф Шумпетер за свое краткое пребывание на посту министра финансов потерпел сокрушительное фиаско.

Драматург, физик, экономист, даже журналист — юный Карл Менгер успел попробовать себя во многих занятиях, прежде чем нашел свое подлинное métier [303] 303 Здесь — призвание (фр.). : математику. Определило все событие, произошедшее во время третьего семестра обучения в университете. Недавно назначенный профессор Ганс Ган проводил первое занятие своего семинара — введение в теорию кривых. Что такое кривая, интуитивно понятно каждому, говорил Ган, однако математически безупречное определение до сих пор ускользает от ученых, а некоторые видные математики сомневаются, можно ли вообще его дать. Долгое время считалось, что кривая — то, что получается, когда проводишь непрерывную линию идеальным, бесконечно тонким пером. Однако Джузеппе Пеано и Давид Гильберт показали, к изумлению коллег, что непрерывная линия, проведенная таким образом, может описывать такую извилистую траекторию, что пройдет через все до единой точки внутри, например, квадрата или куба (подобные линии так и называются — «заполняющие пространство кривые»), и все же никто не станет утверждать, что сплошной квадрат или сплошной куб — это кривая.

Ган применял парадоксальные вымышленные конструкции такого рода, чтобы предостеречь слушателей от опасностей интуитивных представлений: «Ведь, как бы ни говорил Кант, интуицию нельзя считать чистым способом получения априорного знания, скорее это всего лишь сила привычки, коренящаяся в инертности ума» [304] 304 The Crisis in Intuition, 1933, в: Hahn, 1980. .

Как подсказывает здравый смысл, кривая — это что-то одномерное, поверхность — двумерное и так далее. Но как определить саму размерность ? Количеством координат, необходимых, чтобы задать местоположение точки? Тут возникает несколько сложностей. Большинство множеств точек невозможно определить уравнениями, они сложнее, чем обычно считается. И такому определению не удовлетворяют даже самые простые множества точек, например квадрат. Более того, примеры «заполняющих пространство кривых» показывают, что положение точки внутри квадрата задается не двумя числами, а одним (представьте себе бесконечную череду десятичных знаков, скажем, числа π: можно решить, что цифры на нечетных местах задают х -координату точки, а точки на четных — у -координату. Или наоборот — если знать x — и y -координаты каждой точки в квадрате, можно переплести их так, чтобы получилось одно вещественное число). Подобные соображения противоречат интуиции и наталкивают на глубокие вопросы о том, что же на самом деле значит размерность .

Молодой Менгер почти сразу открыл новый подход к загадке о природе «размерности». Основная идея неожиданно проста. Чтобы разрезать трехмерный предмет, например деревянный брусок, берут пилу, и срез получается двумерный. Чтобы разрезать двумерный предмет, например лист бумаги, берут ножницы, и разрез получается одномерный. Чтобы разрезать одномерный предмет, например проволоку, ее несколько раз сгибают туда-сюда кусачками, и срез получается нуль-мерный. Предложение Менгера состояло в том, чтобы определить размерность наоборот — сначала ввести множества нулевой размерности (где срез — пустое множество), затем одномерные, затем двумерные, затем трехмерные, и каждый раз определять высшие размерности через уже определенные низшие (останавливаться на трех, разумеется, нет никаких причин).

Разумеется, облечь эту грубоватую идею в точную математическую форму было нелегко, но вскоре Менгер убедил Ганса Гана, что этот подход сулит успех. И лихорадочно углубился в дальнейшие изыскания.

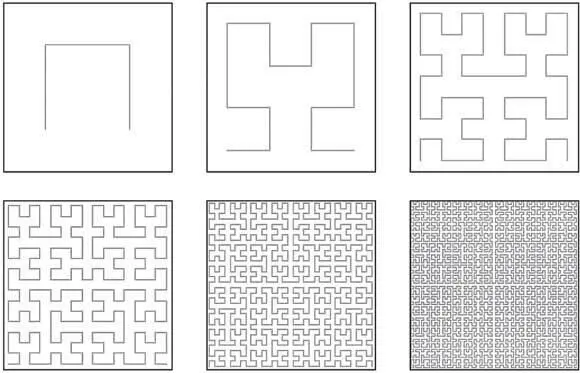
Первые шаги в построении кривой, заполняющей квадрат

Причем немного погодя лихорадка оказалась самой настоящей. Университетские аудитории не отапливались. Нет денег — нет угля. Хрупкое здоровье молодого человека пошатнулось. Диагноз — плеврит.

Восстанавливаться после болезни пришлось долго, и лишь через несколько месяцев Карл Менгер вернулся из отпуска и взялся за работу с прежней страстью. Карл Поппер, который в 1921 году посещал занятия по математике в Венском университете, через семьдесят с лишним лет вспоминал: «На нашем факультете тогда учился Карл Менгер, мой ровесник, но явно гений, полный новых великолепных идей» [305] 305 Popper, 1995. .

Но за этим ударом последовали и другие. Ган нашел ошибку в одном из важнейших доказательств Менгера, и Менгер снова заболел. На сей раз диагноз был страшнее — туберкулез, болезнь, убившая в послевоенные годы очень и очень многих. Врачи даже стали называть его Morbus Viennensis [306] 306 «Венская болезнь» (лат.). . Страшное было время.

Студенты-математики с детства знали о норвежце Нильсе Хендрике Абеле и французе Эваристе Галуа — двух гениальных математиках, чья жизнь трагически оборвалась в юные годы, прежде, чем к ним пришло заслуженное признание: Абель умер от туберкулеза в двадцать семь лет, а Галуа было всего двадцать, когда он скончался через несколько дней после злосчастной дуэли, о которой мы уже говорили. И теперь Карл Менгер поневоле задумывался, не ожидает ли и его та же «романтическая» участь. Прежде чем отбыть обратно в санаторий, он отправил в Академию наук еще одно запечатанное письмо, на сей раз — с описанием математических идей, которые он еще не успел полностью проработать.