Георг Гегель - Наука логики. Том I. Объективная логика

44 К стр. 206. — Имеется в виду шеллингова «система абсолютного тождества», как она развита главным образом в сочинении Шеллинга «Изложение моей системы философии» (1801 г.).

45 К стр. 215. — Намек на сатирическое стихотворение Шиллера «Die Philosophen», 16-е двустишие которого (под заголовком: «Вопрос о праве») гласит: «Jahrelang schon bedien ich meiner Nase zum Riechen;Hab ich denn wirklich an sie auch ein erweisliches Recht?»(«Уже в течение многих лет я пользуюсь своим носом для нюханья, но имею ли я и в самом деле право на это — право, которое можно было бы доказать и обосновать?»).

46 К стр. 223. —В немецком тексте вместо «которого» (dessen) стоит «которой» (deren). Повидимому, это опечатка.

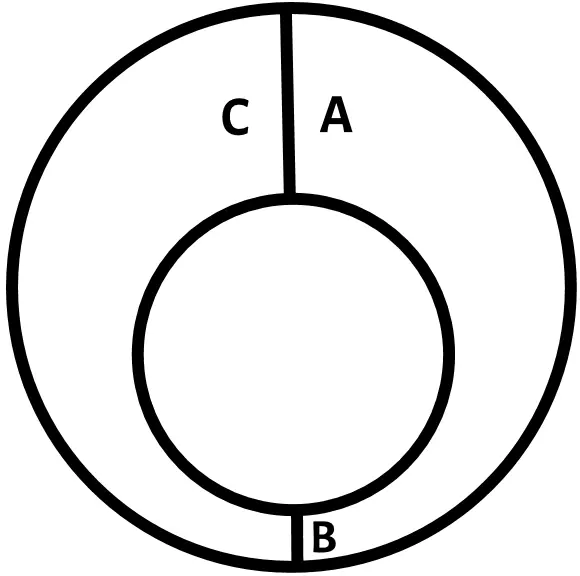
47 К стр. 223. — Фигуру двух неконцентричных кругов (см. рис.), заимствованную у Декарта («Принципы философии», часть II, § 33), Спиноза изобразил, в виде виньетки, на титульном листе своего геометрического изложения «Принципов философии Декарта» (вышло в Амстердаме в 1663 г.), а не «Этики», как ошибочно утверждает Гегель.

48 К стр. 223. — Гегель дает здесь в весьма вольном переводе и с перестановкой отдельных предложений рассуждения Спинозы о бесконечном множестве неравных расстояний между двумя неконцентричными окружностями (см. Спиноза, Переписка, М. 1932, стр. 78). Конец приводимой Гегелем цитаты у Спинозы гласит: «...природа этой вещи не может быть выражена никаким числом».

49 К стр. 246. — В немецком тексте вместо стоит , а вместо напечатано 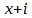. Явная опечатка.

50 К стр. 256. — Проверка с помощью числа девять — громоздкий искусственный прием, в настоящее время вышедший из употребления, ввиду своей непрактичности.

51 К стр. 256. — т. е. «ведь эти члены не будут иметь никакого значения» (или: « никакого веса», « никакой силы»).

52 К стр. 262. — См. стр. 221–222.

53 К стр. 266. — Под «Entwicklungspotenz» Гегель, как видно из этого места, а также из первого абзаца следующего примечания («Еще другие формы, находящиеся в связи с качественной определенностью величины», — стр. 272), понимает то же самое, что в других местах он обозначает терминами: «Entwicklungsglied» (член ряда, получающегося при разложении двучлена 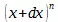по формуле Ньютона), «Entwicklungsfunktion» (функция, получающаяся в результате разложения в ряд,— «функция развертывания», как иногда приходится переводить это выражение: см. напр. стр. 264), «die Funktion der Potenzierung» (функция возвышения в степень), «abgeleitete Funktion» (производная функция,— обычный в математике термин для обозначения того, о чем здесь идет речь у Гегеля). Употребляя для обозначения производной функции несколько странное выражение «Entwicklungspotenz», Гегель, повидимому, хочет подчеркнуть существенное значение того обстоятельства, что дело идет тут именно о степенных функциях, о разложении по степеням , о том, что интересующая нас переменная величина имеет степень выше первой (см. выше, стр. 250). Поэтому как первоначальную, так и производную функцию Гегель называет « степенными функциями» (Potenzenfunktionen).

В связи с этим нельзя не привести отзыв Энгельса. В письме Марксу от 18 августа 1881 г. Энгельс, говоря о математических рукописях Маркса, замечает по поводу математических примечаний Гегеля: «Старик Гегель... вполне правильно угадал, говоря, что диференцирование в виде основного условия требует, чтобы обе переменных имели различные степени и чтобы по меньшей мере одна из них была во второй или ½-й степени. Теперь мы уже знаем почему». ( Маркс и Энгельс , Соч., т. XXIV, стр. 531–532).

54 К стр. 272. — См. прим. 53.

55 К стр. 277. — В немецком тексте вместо «verglichen» стоит «vergleichen». Повидимому, это опечатка.

56 К стр. 287. —Здесь слово «нуль» употребляется Гегелем в фигуральном смысле — в том смысле, что сторона обратного отношения перестает быть стороной отношения, если она становится равной показателю. В математическом же смысле, если мы возьмем обратное отношение, показателем которого является произведение членов отношения и приравняем один из членов отношения этому произведению (например, 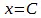), то другой член отношения будет не нулем, а единицей (у = 1). В арифметическом обратном отношении (о котором здесь у Гегеля еще нет речи и формулой которого является х + у = С ), действительно, если х = C , то у = 0 .

57 К стр. 289. — В немецком тексте вместо «keine» (никакой) стоит «eine». Повидимому, это опечатка.

58 К стр. 291. — В издании Лассона эта часть фразы дается по 1-му изданию «Науки логики», где эта фраза гласит: «И вот определенное количество, которое отныне уже не есть безразличное или внешнее определение, а дано так, что оно вместе с тем снято как такое определение...» и т. д.

59 К стр. 292. — Гегель имеет в виду философию Шеллинга.

60 К стр. 300. — Английское слово «фут» означает прежде всего «нога, ступня», а затем уже «фут» в смысле меры длины, приблизительно соответствующей длине ступни человека (30,5 см ). То же самое имеет место и в немецком языке со словом «Fuss».

61 К стр. 303. — Слово «правило» (die Regel) Гегель употребляет здесь в смысле «мерило», «масштаб», «норма», «образцовая или указная мера» (Massregel, Richtmass). В XVIII в. слово «Regel» иногда употреблялось в смысле линейки с делениями. Гегель, повидимому, и намекает на это старинное значение.

62 К стр. 311. — Гегель рассматривает здесь понятие физической константы , т. е. того эмпирического коэфициента, который в той или иной форме входит в уравнения механики и физики. В качестве примера такой константы Гегель в следующей фразе приводит величину а в уравнении движения падения тел 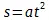. Гораздо чаще формулу движения падения тел выражают уравнением 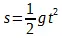, где константа g (постоянное для данного географического пункта ускорение силы тяжести) равна приблизительно 9,8 м (в качестве единицы времени берется при этом секунда). Следовательно, величина а в уравнении 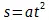равна приблизительно 4,9 м . Впрочем, надо сказать, что величина а или g , входящая в формулу движения падения тел, может быть названа константою лишь в весьма относительном смысле. Дело в том, что сама она изменяется с изменением расстояния от центра земного шара (а также от расположения тяжелых масс на земной поверхности вблизи того места, где производятся опыты с падением тел). Но так как эти изменения весьма незначительны в тех случаях падения тел, которые рассматриваются в элементарной механике (т. е. в тех случаях, где расстояния, проходимые падающим телом, незначительны по сравнению с длиной земного радиуса, причем опыты производятся в одном и том же месте земной поверхности), то ими вполне можно пренебречь.