Вячеслав Кириллов - Логика: учебник для юридических вузов

2. В отрицающем модусе(modus tollens) посылка, выраженная категорическим суждением, отрицает истинность следствия условной посылки, а заключение отрицает истинность основания. Рассуждение направлено от отрицания истинности следствия к отрицанию истинности основания.

Схема модуса:

(2)

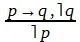
Пример:

Если иск предъявлен недееспособным лицом ( р), то суд оставляет иск без рассмотрения ( q).

Суд не оставил иск без рассмотрения ( не-q).

_________________________

Неверно, что иск предъявлен недееспособным лицом ( не-р) [37] Так как двойное отрицание равнозначно утверждению, вывод можно записать так: «Иск предъявлен дееспособным лицом». .

Нетрудно установить, что возможны еще две разновидности условно-категорического силлогизма: от отрицания истинности основания к отрицанию истинности следствия (3) и от утверждения истинности следствия к утверждению истинности основания (4) [38] Модусы могут быть представлены в записи: 1) ((p → q) ∧ p) → q ; 2) ((p → q) ∧ ˥q) → ˥p ; 3) ((р → q) ∧ ˥р) → ˥q ; 4) ((p → q) ∧ q) → p. , т. е.:

(3)

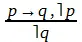
(4)

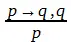
Однако заключение по этим модусам не будет достоверным. Так, если в примере, приведенном выше, основание условной посылки отрицается: неверно, что иск предъявлен недееспособным лицом (схема 3), нельзя с достоверностью отрицать истинность следствия: неверно, что суд оставляет иск без рассмотрения. Суд может оставить иск без рассмотрения и по другим обстоятельствам, например, в результате истечения срока исковой давности.

Утверждение следствия: суд оставляет иск без рассмотрения (схема 4) не влечет с необходимостью истинность основания: суд может оставить иск без рассмотрения не только в результате недееспособности истца, но и по другим причинам.

Итак, из четырех модусов условно-категорического умозаключения, исчерпывающих все возможные комбинации посылок, достоверные заключения дают два: утверждающий (modus ponens) (1) и отрицающий (modus tollens) (2). Они выражают законы логики и называются правильными модусами условно-категорического умозаключения. Эти модусы подчиняются правилу: утверждение основания ведет к утверждению следствия и отрицание следствия — к отрицанию основания. Два других модуса (3 и 4) достоверных заключений не дают. Они называются неправильными модусами и подчиняются правилу: отрицание основания не ведет с необходимостью к отрицанию следствия и утверждение следствия не ведет с необходимостью к утверждению основания.

При анализе условно-категорического умозаключения нужно иметь в виду следующее. Во-первых, основание и следствие большей посылки может быть как утвердительным, так и отрицательным суждением: p → q; ˥p → q; p → ˥q; ˥p → ˥q. Например:

Если состав преступления отсутствует ( р), то уголовное дело не может быть возбуждено ( ˥q).

Состав преступления отсутствует ( р).

__________________

Уголовное дело не может быть возбуждено ( ˥q).

Следствие условной посылки — отрицательное суждение, категорическая посылка (утвердительное суждение) утверждает истинность основания, заключение (отрицательное суждение) утверждает истинность следствия, т. е.

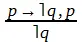
Это утверждающий модус.

Возможны и другие разновидности модусов.

Во-вторых, если бóльшая посылка является эквивалентным суждением: р ≡ q(если, и только если р, то q), где ≡— знак эквивалентности, то достоверные заключения получаются по всем четырем модусам:

; ; ;

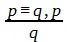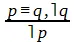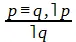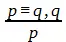
’ iq ’ P

Рассмотрим для примера выделяющее условное суждение: «Если лицо виновно в совершении преступления, то оно подлежит уголовной ответственности». Нетрудно установить, что достоверное заключение получается по любому из приведенных модусов.

Необходимость вывода по утверждающему и отрицающему модусам можно показать с помощью таблиц истинности.

Утверждающий модус(таблица 15).

Истинность импликации (столбик 3) зависит от истинности антецедента (основания) (1) и консеквента (следствия) (2). Импликация считается ложной тогда и только тогда, когда антецедент истинен, а консеквент ложен (2-я строка таблицы). Во всех остальных случаях импликация истинна. Истинность или ложность конъюнкции (4-й столбик) также зависит от составляющих ее членов (3 и 1). Конъюнкция истинна тогда и только тогда, когда истинны оба ее члена (1 -я строка таблицы).

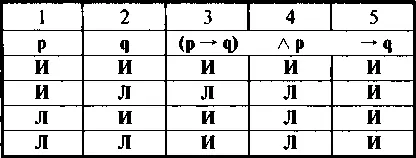
Таблица 15

Теперь установим истинность импликации (5-й столбик таблицы — утверждающий модус). Так как импликация антецедента (4) и консеквента (2) не содержит случая, когда антецедент истинен, а консеквент ложен, то импликация всегда истинна. Следовательно, высказывание ((р → q) ∧ р) → qявляется логическим законом.

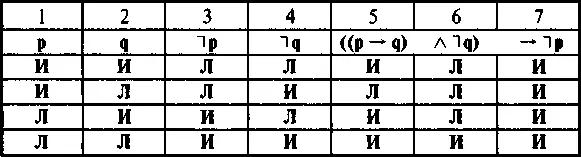
Отрицающий модус(таблица 16).

В столбиках 1 и 3,2 и 4 показано, что если одно высказывание ложно, то его отрицание истинно. Импликация ри q(1 и 2) ложна только в одном случае (2-я строка таблицы) — столбик 5. Конъюнкция (столбик 6) высказываний ( р → q) и ˥q(5 и 4) истинна только в одном случае (4-я строка таблицы). Импликация ((р → q) ∧ ˥q)и ˥р(6 и 3) всегда истинна, так как не содержит случая, когда антецедент истинен, а консеквент ложен. Следовательно, высказывание ((p → q) ∧ ˥q) → ˥pявляется логическим законом.

С помощью таблиц истинности можно показать недостоверность выводов по неправильным модусам.

Таблица 16

1. Какое умозаключение называется условным? Как оно строится? На каком правиле основан его вывод?

2. Какие умозаключения называются условно-категорическими? Какие модусы являются правильными и какие неправильными? Приведите их схемы.