Юрий Ревич - Занимательная микроэлектроника

Смысл понятия емкости раскрывается так: если напряжение от источника напряжения составляет 1 В, то емкость в одну нанофараду, как у лейденской банки, может запасти 10 -9кулон электричества. Если напряжение составит 10 5вольт (типичная величина при заряде от электростатической машины, как в опытах Мушенбрука), то и запасенный на данной емкости заряд увеличится в той же степени — до 10 -4кулон. Любой конденсатор фиксированной емкости сохраняет это соотношение: заряд на нем тем больше, чем больше напряжение, а коэффициент пропорциональности в этой зависимости определяется номинальной емкостью.

Если замкнуть конденсатор на резистор, то в первый момент времени он будет работать, как источник напряжения с нулевым выходным сопротивлением и номинальным напряжением той величины, до которой конденсатор был заряжен. Таким образом ток через резистор в начальный момент времени определяется по обычному закону Ома. Скажем, в случае гвардейцев Мушенбрука характерное сопротивление цепи из нескольких человек, взявшихся за руки, составляет порядка 10 4Ом, т. е. ток при начальном напряжении на конденсаторе 10 5В составит 10 А, что примерно в 1000 раз превышает смертельное для человека значение тока! Выручило гвардейцев то, что такой импульс был крайне кратковременным, поскольку по мере разряда конденсатора, т. е. утекания заряда с пластин, напряжение быстро снижается (емкость-то остается неизменной, потому при снижении заряда, согласно формуле на рис. 2.7, падает и напряжение).

Заметки на полях

Интересно, что при фиксированном заряде (если цепь нагрузки конденсатора отсутствует) можно изменить напряжение на нем, меняя емкость — например, при раздвижении пластин плоского конденсатора емкость его падает (т. к. расстояние d между пластинами увеличивается), потому для сохранения заряда, согласно сказанному, напряжение должно увеличиться — что и происходит на деле (в эффектном школьном опыте между раздвигаемыми пластинами конденсатора проскакивает искра, когда напряжение превышает предельно допустимое напряжение пробоя для воздуха).

На рис. 2.8 изображено подключение конденсатора С к нагрузке R .

Рис. 2.8. Подключение конденсатора к нагрузке:

К— переключатель, Б— батарея, С— конденсатор, R— сопротивление нагрузки

Первоначально переключатель К ставят в нижнее по схеме положение и конденсатор заряжается до напряжения батареи Б . При переводе переключателя в верхнее положение конденсатор начинает разряжаться через сопротивление R и напряжение на нем снижается. Насколько быстро происходит падение напряжения при подключении нагрузки? Можно предположить, что чем больше емкость конденсатора и сопротивление резистора нагрузки, тем медленнее происходит падение напряжения. Правда ли это?

Это легко оценить через размерности связанных между собой электрических величин — тока, емкости и напряжения. В самом деле, в определение тока входит и время (напомним, что ток есть заряд, протекающий за единицу времени), которое нас и интересует. Если вспомнить, что размерность емкости есть кулон на вольт, то искомое время можно попробовать описать формулой: t= C∙ U/ I, где С — емкость, a U и I — ток и напряжение соответственно (проверьте размерность!).

Для случая, изображенного на рис. 2.8, эта формула справедлива на малых отрезках времени, пока ток I не падает значительно из-за уменьшения напряжения на нагрузке. Отметим, что данная формула полностью справедлива и на больших отрезках времени, если ток разряда (или заряда) конденсатора стабилизировать, что означает подключение его к источнику втекающего (при разряде) или вытекающего (при заряде) тока.

При фиксированной обычной нагрузке с сопротивлением R (помните, мы говорили, что простой резистор есть плохой источник тока?) так, конечно, не происходит — напряжение на конденсаторе падает по мере истощения заряда, соответственно ток через нагрузку также пропорционально снижается — в полном соответствии с законом Ома. Опять приходится брать интегралы, потому мы приведем только конечный результат: формула для расчета процесса снижения напряжения на емкости при разряде ее через резистор и соответствующий график показаны на рис. 2.9, а . На рис. 2.9, б показан аналогичный процесс, который происходит при заряде емкости через резистор.

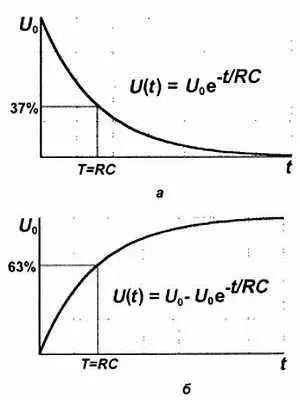
Рис. 2.9. Процессы при разряде ( а) и заряде ( б) конденсатора:

С— емкость, R— сопротивление нагрузки, t— время, e— основание натуральных алгоритмов (2,718282)

Нужно отметить два момента. Во-первых, если сопротивление резистора R на рис. 2.8 (если включить в него как сопротивление проводов и ключа, так и — при заряде — внутреннее сопротивление батареи) не равно нулю, то получается, что процессы разряда и заряда по рис. 2.9 длятся бесконечно? Да, теоретически полностью конденсатор не разрядится и не зарядится никогда, но практически это почти не имеет значения, потому что напряжение на конденсаторе становится близким к нулю или к напряжению питания очень быстро.

Во-вторых, из формул на рис. 2.9 следует очень интересный вывод: если сопротивление R равно нулю, то время процесса разряда или заряда становится бесконечно малым, а ток через нагрузку, согласно закону Ома, бесконечно большим! Обратимся снова к рис. 2.8, нечто подобное должно происходить при переключении ключа К в положение заряда емкости от батареи. Естественно, в реальной жизни ни о каких бесконечных токах речи не идет, для этого батарея должна иметь нулевое выходное сопротивление, т. е. бесконечно большую мощность (подумайте, почему эти утверждения равносильны?), а проводники должны обладать нулевым сопротивлением. Поэтому на практике процесс заряда от источника (и разряда при коротком замыкании пластин) происходит за малое, но конечное время, а ток, хоть и не бесконечно велик, но все же может достигать очень больших значений.

Значение тока в первый момент при включении конденсатора в цепь очень важно для практики. Например, под него надо рассчитывать кратковременную перегрузочную способность источника питания — иначе вы ничего не сможете включить в такой источник, потому что в первое же мгновение сработает защита, несмотря на то, что номинально мощности должно хватать. Как рассчитать этот ток? Для этого нужно представить, что конденсатор при заряде в первый момент времени ведет себя так, как будто цепь в месте его установки замкнута накоротко (это очень точное представление!). Тогда ток определится просто по закону Ома, в который подставляется сопротивление проводов и контактов (плюс, если это требуется, внутреннее сопротивление источника).