Юрий Ревич - Занимательная электроника

Другой пример: обычные часы с цифровым дисплеем. Все мы уже к этому делу привыкли, но ведь большинство практических задач заключаются не в определении точного времени, а в определении интервала — сколько мы уже ждем, или сколько осталось до некоторого момента. Для этого знания точного значения часов и минут не требуется, и обладателю часов с цифровым дисплеем приходится в уме производить довольно сложные арифметические действия, вычисляя этот интервал, вместо того чтобы просто мысленно передвинуть стрелки на циферблате. Как видите, проектирование показывающих устройств не слишком простое дело, т. к. не может производиться только из соображений компактности схемы или высокой точности измерений, а непременно должно учитывать требования эргономики и « usability » — удобства пользования. Если читателю кажется, что меня очередной раз занесло несколько в сторону от темы книги, то это не так, потому что проектирование аналого-цифровых и особенно цифроаналоговых устройств неразрывно связано с проблемами человеко-машинного взаимодействия — не будь потребителя, незачем все это было бы и затевать. Компьютеры в общении между собой спокойно обойдутся и двоичным кодом.

Займемся сначала общими принципами аналого-цифрового преобразования. Основной принцип оцифровки любых сигналов очень прост и показан на рис. 17.1, а . В некоторые моменты времени t 1, t 2, t 3 мы берем мгновенное значение аналогового сигнала и как бы прикладываем к нему некоторую меру, линейку, проградуированную в двоичном масштабе. Обычная линейка содержит крупные деления (метры), поделенные каждое на десять частей (дециметры), каждая из которых также поделена на десять частей (сантиметры), и т. д. Двоичная линейка содержала бы деления, поделенные пополам, затем еще раз пополам и т. д. — сколько хватит разрешающей способности. Если вся длина такой линейки составляет, допустим, 2,56 м, а самое мелкое деление — 1 см (т. е. мы можем померить ей длину с точностью не хуже 1 см, точнее, даже половины его), то таких делений будет ровно 256, и их можно представить двоичным числом размером 1 байт или 8 двоичных разрядов.

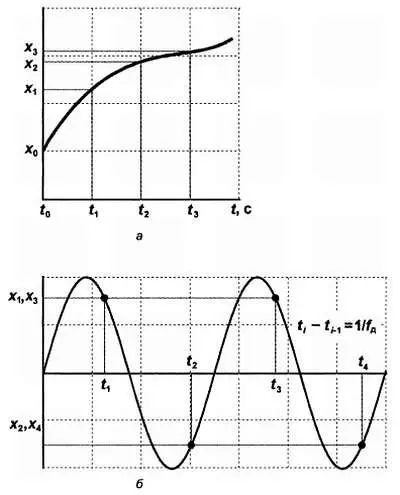
Рис. 17.1. Оцифровка аналоговых сигналов:

а— основной принцип;

б— пояснение к теореме Котельникова — Найквиста

Ничего не изменится, если мы меряем не длину, а напряжение или сопротивление, только смысл понятия «линейка» будет несколько иной. Так мы получаем последовательные отсчеты величины сигнала x 1, x 2, x 3 . Причем заметьте, что при выбранной разрешающей способности и числе разрядов мы можем померить величину не больше некоторого значения, которое соответствует максимальному числу, в данном случае 255. Иначе придется или увеличивать число разрядов (удлинять линейку), или менять разрешающую способность в сторону ухудшения (растягивать ее). Все изложенное и есть сущность работы аналого-цифрового преобразователя — АЦП.

На рис. 17.1, а график демонстрирует этот процесс для случая, если мы меряем какую-то меняющуюся во времени величину. Если измерения производить регулярно с известной частотой (ее называют частотой дискретизации или частотой квантования), то записывать можно только значения сигнала. Если стоит задача потом восстановить первоначальный сигнал по записанным значениям, то, зная частоту дискретизации и принятый масштаб (т. е. какому значению физической величины соответствует максимальное число в принятом диапазоне двоичных чисел), мы всегда можем восстановить исходный сигнал, просто отложив точки на графике и соединив их плавной линией.

Но что мы при этом теряем? Посмотрите на рис. 17.1, б , который иллюстрирует знаменитую теорему Котельникова (как водится, за рубежом она носит другое имя — Найквиста, на самом деле они оба сформулировали ее независимо друг от друга). На этом рисунке показана синусоида предельной частоты, которую мы еще можем восстановить, располагая массивом точек, полученных с частотой дискретизации f д . Так как в формуле для синусоидального колебания A ·sin(2π ft ) имеется два независимых коэффициента ( А — амплитуда и f — частота), то для того чтобы вид графика восстановить однозначно, нужно как минимум две точки на каждый период [24] Если сами параметры синусоиды А и f не меняются во времени, то достаточно вообще двух точек на все время. Именно такой случай показан на графике рис. 17.1, б . , т. е. частота оцифровки должна быть как минимум в два раза больше, чем самая высокая частота в спектре исходного аналогового сигнала . Это и есть одна из расхожих формулировок теоремы Котельникова — Найквиста.

Попробуйте сами нарисовать другую синусоиду без сдвига по фазе, проходящую через указанные на графике точки, и вы убедитесь, что это невозможно. В то же время можно нарисовать сколько угодно разных синусоид, проходящих через эти точки, если их частота в целое число раз выше частоты дискретизации f д . В сумме эти синусоиды, или гармоники (т. е. члены разложения сигнала в ряд Фурье — см. главу 5 ), дадут сигнал любой сложной формы, но восстановить их нельзя, и если такие гармоники присутствуют в исходном сигнале, то они пропадут навсегда.

Только гармонические составляющие с частотами ниже предельной восстанавливаются однозначно. То есть процесс оцифровки равносилен действию ФНЧ с прямоугольным срезом характеристики на частоте, равной ровно половине частоты дискретизации.

Теперь об обратном преобразовании. В сущности, никакого преобразования цифрааналог в ЦАП, которые мы будем здесь рассматривать, не происходит, просто мы выражаем двоичное число в виде пропорциональной величины напряжения, т. е. занимаемся, с точки зрения теории, всего лишь преобразованием масштабов. Вся аналоговая шкала поделена на кванты — градации, соответствующие разрешающей способности нашей двоичной «линейки». Если максимальное значение сигнала равно, к примеру, 2,56 В, то при восьмиразрядном коде мы получим квант в 10 мВ, и что происходит с сигналом между этими значениями, а также и в промежутки времени между отсчетами, мы не знаем и узнать не можем. Если взять ряд последовательных отсчетов некоего сигнала, например, тех, что показаны на рис. 17.1, а , то мы в результате получим ступенчатую картину, показанную на рис. 17.2.

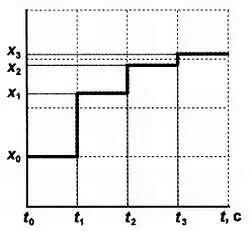
Рис. 17.2. Восстановление оцифрованного сигнала с рис. 17.1, а

Если вы сравните графики на рис. 17.1, а и на рис. 17.2, то увидите, что второй график представляет первый, мягко говоря, весьма приблизительно. Для того чтобы повысить степень достоверности полученной кривой, следует, во-первых, брать отсчеты почаще, и во-вторых, увеличивать разрядность. Тогда ступеньки будут все меньше и меньше, и есть надежда, что при некотором достаточно высоком разрешении, как по времени, так и по квантованию, кривая станет, в конце концов, неотличима от непрерывной аналоговой линии.