Чарльз Платт - Электроника для начинающих (2-е издание)

Описанное простое сочетание конденсатора и резистора называется резистивно-емкостной цепочкой (или RC-цепочкой, R — резистор, С — конденсатор). Это очень важное понятие в электронике. Прежде чем я объясню, что она делает, вот несколько вопросов для размышления:

• Точно ли в 10 раз дольше заряжался конденсатор до напряжения 9 В при замене резистора номиналом 1 кОм на резистор 10 кОм?

• Постоянной ли была скорость роста напряжения на конденсаторе или же оно увеличивалось быстрее в начале эксперимента (или, наоборот, ближе к окончанию)?

• Как вы считаете, если подождать достаточно долго, сможет ли напряжение на конденсаторе достичь напряжения батареи?

Представьте, что резистор — это вентиль, ограничивающий поток воды, а конденсатор — это резиновый шарик, который вы пытаетесь наполнить (рис. 2.77). Если вы закроете вентиль до такой степени, что вода просачивается по каплям, шарик будет заполняться очень долго. Но небольшой поток воды все же может наполнить емкость, если вы подождете достаточно долго. Если предположить, что шарик не лопнет, процесс закончится, когда давление внутри шарика сравняется с давлением воды в трубе, которая подает воду через вентиль.

Но здесь упущен из виду один важный фактор. По мере того как шарик наполняется, оболочка растягивается, оказывая большее давление на его содержимое. С увеличением давления внутри шарика оно выталкивает входящий поток воды. Следовательно, мы можем ожидать, что с течением времени вода будет заполнять резервуар все медленнее.

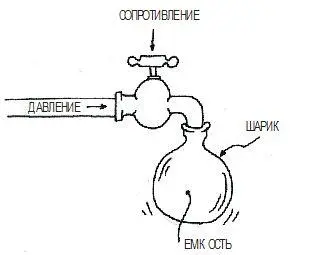
Как это соотносится с электронами, стремящимися в конденсатор? Концепция аналогична. Сначала электроны стремительно поступают, но по мере заполнения пространства новоприбывшим требуется больше времени на поиск свободного места. Процесс заряда становится все медленнее и медленнее. На самом деле, напряжение на конденсаторе теоретически никогда не сравняется с подаваемым на него напряжением.

Скорость, с которой заряжается конденсатор, зависит от параметра, известного как «постоянная времени». Определение очень простое:

ТС = R × С

Здесь ТС — постоянная времени, в секундах, если конденсатор с номиналом С (измеряемым в фарадах) заряжается через резистор с номиналом R (в омах).

Вернемся к схеме, которую вы тестировали вначале, используя резистор номиналом 1 кОм. Можно подставить номиналы компонентов в формулу для постоянной времени, только при этом следует перевести единицы измерения в омы и фарады. Так, 1 кОм равен 1000 Ом, а 1000 мкФ — это 0,001 фарада. Поэтому получить результат проще простого:

ТС = 1000 × 0,001

Следовательно, для таких номиналов резистора и конденсатора ТС = 1 с.

Но что означает полученный результат? Значит ли это, что конденсатор будет заряжен полностью за одну секунду? К сожалению, не все так просто.

На самом деле постоянная времени ТС — это время (в секундах), необходимое конденсатору для того, чтобы напряжение на нем составило 63% от подаваемого напряжения, если заряд начался с нулевого напряжения.

А что если конденсатор заряжается не с нуля? Если мы начинаем измерения после того как конденсатор уже приобрел некоторое напряжение, определение становится немного сложнее. Если V DIF— это разность между напряжением конденсатора и подаваемым напряжением, то ТС — это интервал времени (в секундах), необходимый для добавления 63% величины V DIFк его текущему значению.

Замечание

Почему 63%? Почему не 62? Или 64? Или 50? Ответ на этот вопрос слишком сложен для данной книги, и вам придется почитать о постоянных времени где-либо еще, если вы захотите узнать больше. Приготовьтесь к изучению дифференциальных уравнений.

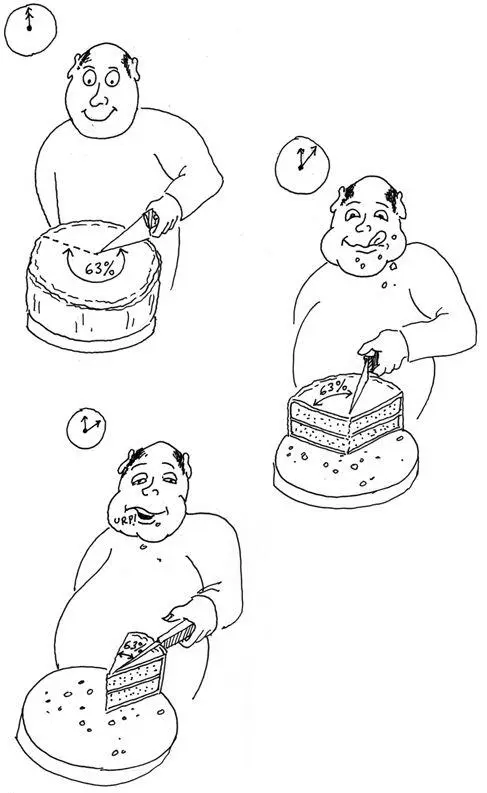
Для простоты используем такую аналогию. На рис. 2.78 вы видите лакомку, которому достался вкусный торт. Вначале наш гурман очень голоден, и поэтому он отрезает 63% от торта и съедает этот кусок за одну секунду — это его «постоянная времени» поедания торта. Во второй заход он берет 63% от оставшегося торта; а поскольку он уже не настолько голоден, ему требуется еще одна секунда (помните о том, что это его постоянная времени). В третий раз он опять отрезает 63% от остатка и снова поедает его за секунду. И так далее. Желудок постепенно наполняется тортом, подобно тому, как конденсатор наполняется электронами. Но он никогда не съест весь торт, потому что всегда берет только 63% от остатка.

На рис. 2.79 этот процесс показан еще одним способом. По истечении каждой константы времени (которая равна 1 секунде, если у нас конденсатор емкостью 1000 мкФ и резистор 1 кОм) конденсатор получает 63% разности между текущим напряжением и напряжением, подаваемым от источника питания.

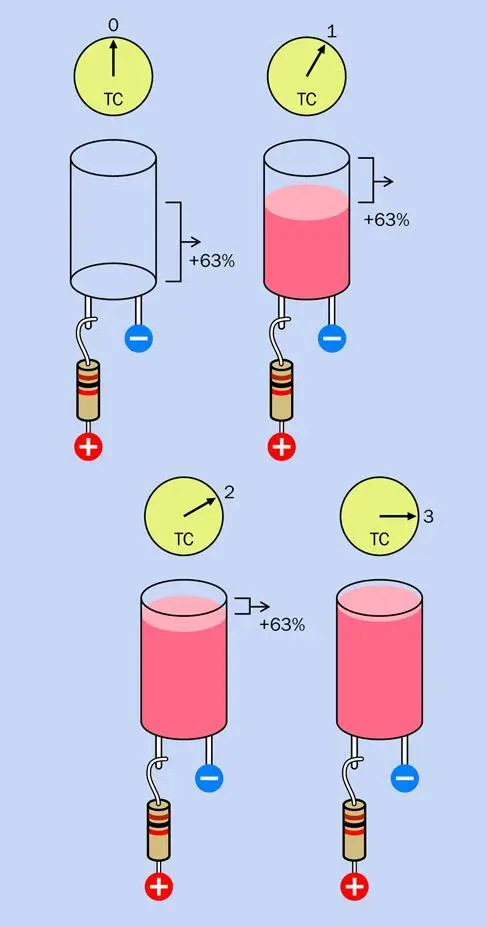
В мире идеальных компонентов процесс заряда будет продолжаться бесконечно. Но в реальных условиях мы считаем, что по истечении временного интервала, равного пяти постоянным времени, заряд конденсатора приблизится к 100%, и можно считать процесс завершенным.

Мне хотелось бы начертить график, показывающий напряжение на обкладках конденсатора по мере его заряда. Чтобы сделать это, я рассчитаю необходимые значения с помощью формулы для постоянной времени.

Предположим, V CAP— это напряжение на конденсаторе в данный момент, a V DIF— разность между текущим напряжением на конденсаторе и напряжением питающей батареи. Приведенная далее формула даст ответ на вопрос, каким будет новое напряжение конденсатора по прошествии одной постоянной времени. Обозначим это новое напряжение как V NEW. Формула выглядит следующим образом:

Величина 0,63 означает то же, что и 63%.

Предположим, батарея выдает ровно 9 В, а конденсатор начал заряжаться с нулевого напряжения. Итак, V CAP= 0, a V DIF= 9. Подставим эти значения в формулу:

V NEW= 0 + (0,63 × 9)

Расчет на калькуляторе дает 0,63 × 9 = 5,67. Поэтому по истечении одной постоянной времени (одной секунды с резистором номиналом 1 кОм и конденсатором емкостью 1000 мкФ) на конденсаторе будет напряжение 5,67 В.