Вадим Грибунин - Цифровая стеганография

.

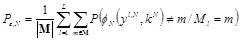Если в результате действий нарушителя в произвольном экземпляре стего за номером l , где 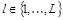, детектор обнаруживает идентификационный номер, не принадлежащий множеству 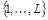, то это значит, что нарушитель способен переложить ответственность за несанкционированное копирование на невиновного пользователя. Нарушитель также добился успеха, если детектор не обнаруживает никакого идентификационного номера. Любой из этих фактов классифицируется как взлом стегосистемы идентификационных номеров. Назовем совершенной стегосистемой идентификационных номеров систему, обеспечивающую нулевую вероятность ошибочного декодирования при ограничении искажений контейнера, вносимых атакующим, величиной при условии, что число доступных атакующему экземпляров 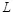бесконечно велико.

Также введем определение стойкой стегосистемы идентификационных номеров, для которой неравенство 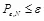, где 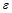есть допустимое ненулевое значение, выполняется при ограничении искажений, вносимых атакующим, величиной при условии, что атакующему доступно конечное число L заверенных экземпляров. Определим такую стегосистему идентификационных номеров 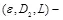стойкой. Например, для практически востребованных стегосистем вероятность ошибочного декодирования идентификационных номеров, то есть вероятность успеха нарушителя, может быть задана величиной 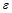порядка 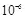… 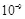, для заверяемых изображений допустимая величина искажения может быть получена из величины отношения средней мощности сигнала контейнера к величине не хуже 40–45 дБ, а число доступных злоумышленникам экземпляров L не более десятков-сотен. Предположим, что этот пример описывает задачу защиты имущественных прав фирмы-производителя, продающей лицензионные записи видеофильма на DVD-дисках. Величина L в этом случае ограничивается бюджетом коалиции злоумышленников, пытающихся стереть аутентифицирующую информацию с видеозаписи и тиражировать для продажи «пиратские» копии. Им невыгодно покупать слишком много экземпляров, так как доходы от нелегального бизнеса могут не покрыть расходы на приобретение дорогостоящих DVD-дисков. Злоумышленники вынуждены сами ограничивать величину искажений , так как иначе низкокачественные контрафактные видеозаписи никто не купит. И если вероятность успеха злоумышленников не превышает значения порядка 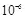, то этот вид преступного бизнеса оказывается бессмысленным.

Скорость передачи R идентификационных номеров и скрытая ПС стегоканала передачи идентификационных номеров определяется так же, как и для ранее описанных систем ЦВЗ.

Рассмотрим известные результаты для систем идентификационных номеров.

Теорема 3.12: При любой атаке нарушителя, приводящей к искажению , скорость передачи R идентификационных номеров достижима, если и только если 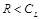, где величина скрытой ПС стегоканала передачи идентификационных номеров 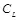определяется в соответствии с выражением (3.28). Пусть используется симметричная функция искажений 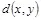, величина искажения превышает величину искажения кодирования 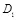, 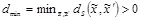для некоторого значения 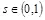, где 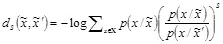есть расстояние Чернова между распределениям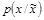и и 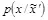. Тогда скрытая ПС 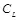экспоненциально быстро стремится к нулю со скоростью, ограниченной снизу величино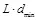й при .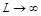

В работе [2] указывается, что оптимальное атакующее воздействие не имеет памяти, и что экспоненциальное уменьшение скрытой ПС с ростом L справедливо для любого распределения контейнеров 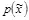. Быстрое уменьшение величины скрытой ПС при увеличении числа доступных нарушителю экземпляров свидетельствует о том, что трудности построения стойких систем идентификационных номеров существенно превышают трудности построения стойких систем ЦВЗ. Можно сказать, что для обычной системы ЦВЗ значение 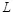равно единице. В работах [28,30] приводятся примеры реальных систем идентификационных номеров, оказавшихся слабыми против сговора большого числа 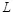пользователей. В соответствии с теоремой 3.12, эти результаты справедливы для большого класса алгоритмов идентификационных номеров.

В атаке сговора злоумышленник для каждого элемента контейнера вычисляет его оценку по правилу максимальной апостериорной вероятности вида 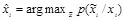. Заметим, что атака на основе максимальной апостериорной вероятности, неэффективная для восстановления хорошей оценки контейнера с гауссовским распределением в обычной системе ЦВЗ (см. пункт 3.4.2), оказалась так эффективна против систем с ИН. Очевидно, это объясняется тем, что атака на систему ИН построена как детерминированная, используя множество заверенных контейнеров для получения одного решения.

В атаке сговора средняя вероятность ошибочного декодирования идентификационного номера уменьшается при увеличении размерности алфавита | X|. Это означает, что шансы сохранить неразрушенным идентификационный номер контейнера существенно возрастают при увеличении размерности алфавита символов контейнера. Этот результат интуитивно понятен, так как чем больше экземпляры стего отличаются друг от друга, тем сложнее нарушителю точно восстановить пустой контейнер. А при малой размерности алфавита | X| больших отличий разных экземпляров стего физически нельзя обеспечить.