Чарльз Петцольд - Код. Тайный язык информатики

Для сложения трех двоичных цифр понадобятся два полусумматора и вентиль ИЛИ, соединенные следующим образом.

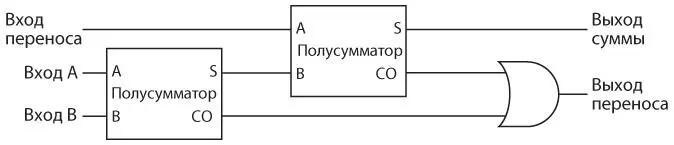
Чтобы разобраться в этой схеме, начнем со входов A и B первого полусумматора слева. Результат — бит суммы и бит переноса. Эта сумма должна быть добавлена к переносу из предыдущего столбца, поэтому они являются входами для второго полусумматора. Сумма, полученная от второго полусумматора, — окончательная. Два переноса из полусумматоров — входы для вентиля ИЛИ. Может показаться, что здесь нужен второй полусумматор, и такая схема, безусловно, сработала бы. Однако если вы проанализируете все возможности, то обнаружите, что оба переноса из двух полусумматоров никогда не равны 1. Вентиля ИЛИ достаточно для их сложения, поскольку он действует так же, как вентиль Искл-ИЛИ, если оба входных сигнала одновременно не равны 1.

Вместо многократного перерисовывания этой схемы можем просто назвать ее полным сумматором.

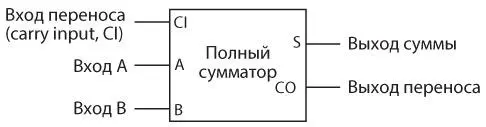
В следующей таблице представлены все возможные комбинации входов для полного сумматора и результирующие выходы.

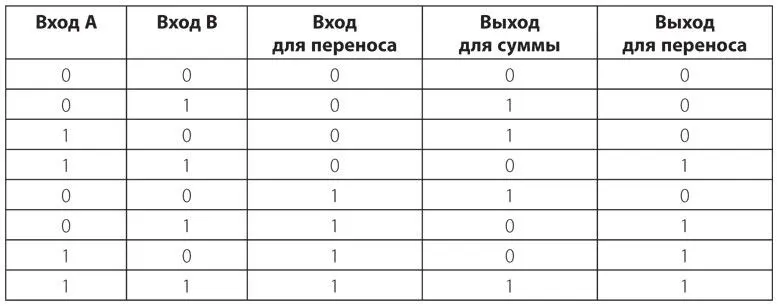
В начале этой главы я сказал, что для создания сумматора потребуются 144 реле. Вот как я это понял: для каждого вентиля И, ИЛИ и И-НЕ требуются по два реле. Таким образом, вентиль Искл-ИЛИ состоит из шести реле. Полусумматор — это вентиль Искл-ИЛИ и вентиль И, поэтому для его создания необходимы восемь реле. Каждый полный сумматор — два полусумматора и вентиль ИЛИ, то есть 18 реле. Нам нужны восемь полных сумматоров для создания 8-битной машины, или 144 реле.

Вспомните наш исходный пульт управления с переключателями и лампочками.

Теперь мы можем начать присоединять переключатели и лампочки к полному сумматору.

Сначала подключим два крайних правых переключателя и крайнюю правую лампочку к полному сумматору.

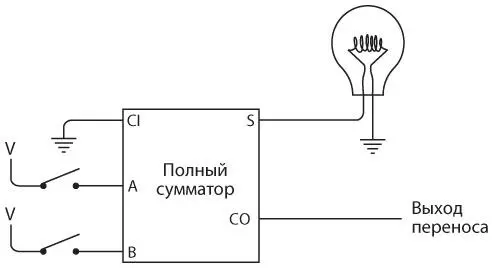
Когда вы начинаете складывать два двоичных числа, первый столбец цифр отличается от остальных тем, что не может содержать бит переноса из предыдущего столбца. В первом столбце нет бита переноса, поэтому вход для переноса полного сумматора соединяется с землей, то есть его значением является 0 бит. Разумеется, в результате сложения первой пары двоичных цифр может получиться бит переноса. Этот выход переноса — вход для следующего столбца.

Для следующих двух цифр и лампочки вы используете полный сумматор, подключенный так.

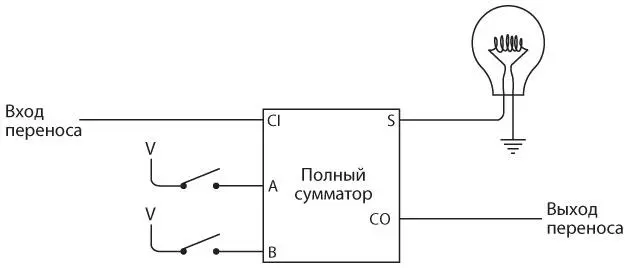
Выход переноса, полученный от первого полного сумматора, является входом для второго полного сумматора. Каждый последующий столбец цифр складывается по той же схеме. Каждый разряд переноса из одного столбца подается на вход для переноса следующего столбца.

Наконец, восьмая и последняя пара переключателей подключена к последнему полному сумматору.

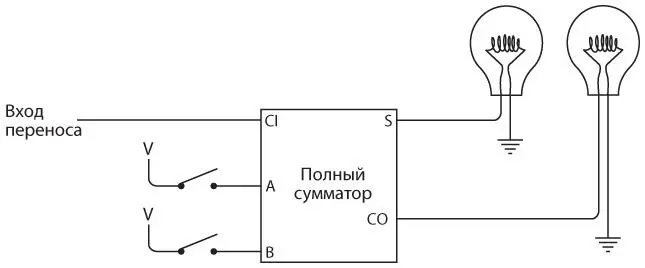
Здесь последний выход для переноса подключен к девятой лампочке.

Вот еще один способ изобразить схему из восьми полных сумматоров (full adder, FA), в которой каждый выход для переноса (CO) подключен к следующему входу для переноса (CI).

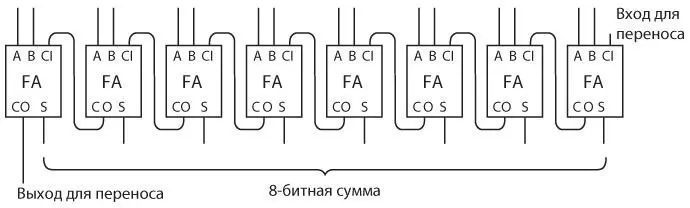
Представим единое обозначение 8-битного сумматора, входы обозначим буквами от A0 до A7 и от B0 до B7, выходы — буквами от S0 до S7 (от sum — «сумма»).

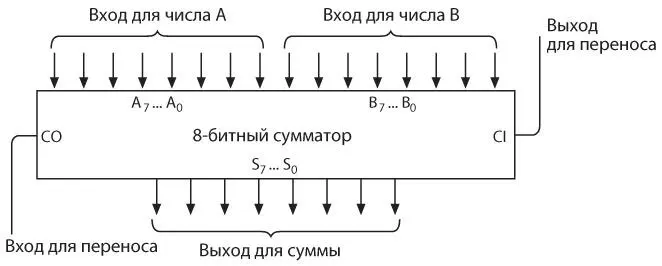
Это распространенный способ обозначения отдельных битов многобитного числа. Биты A0, B0 и S0 являются младшими , а биты A7, B7 и S7 — старшими . Например, вот как с помощью этих букв с индексами можно было бы представить двоичное число 0110 1001.

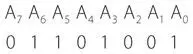
Индексы начинаются с 0 и увеличиваются по мере перехода ко все более значимым цифрам, поскольку они соответствуют показателю степени двойки.

Если вы умножите каждую степень двойки на цифру, расположенную под ней, и сложите результаты, получите десятичный эквивалент числа 0110 1001, который равен 64 + 32 + 8 + 1, или 105.

По-другому 8-битный сумматор можно изобразить так.

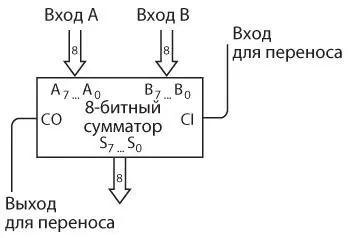
Восьмерки внутри стрелок указывают на то, что каждая из них — это группа из восьми отдельных сигналов. Индексы символов A7 … A0, B7 … B0 и S7 … S0 также обозначают восьмиразрядность числа.

Как только соберете один 8-битный сумматор, вы сможете создать второй. Их легко расположить каскадом , чтобы сложить два 16-битных числа.

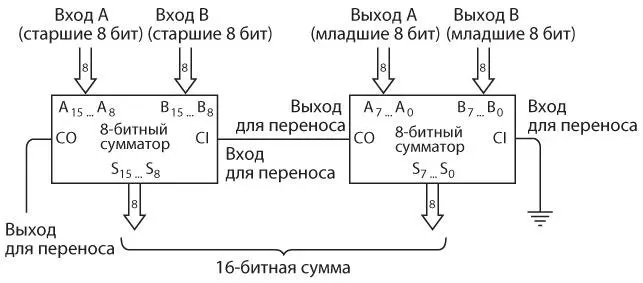
Выход для переноса правого сумматора связан со входом для переноса левого. Левый сумматор в качестве входных значений принимает самые старшие восемь цифр двух слагаемых и в качестве выходного значения выдает самые старшие восемь цифр.

Теперь вы можете спросить: «Неужели компьютеры действительно складывают числа именно так?»

В принципе да. Но не совсем.

Во-первых, сумматоры могут быть быстрее тех, которые мы описали. Если вы посмотрите на то, как работает эта схема, то поймете, что выход переноса от младшей пары цифр необходим для сложения со следующей парой, выход переноса от второй пары цифр — для сложения с третьей парой и т. д. Общая скорость сумматора равна количеству битов, умноженному на скорость одного полного сумматора. Это называется сквозным переносом . Быстрые сумматоры используют дополнительные схемы ускоренного переноса .

Во-вторых (и это самое главное), компьютерам больше не нужно реле! Однако первые цифровые компьютеры, созданные в начале 1930-х годов, использовали реле, позднее — вакуумные лампы. Современные компьютеры создаются на основе транзисторов. Транзисторы в основном функционируют так же, как и реле, однако (как мы увидим далее) они намного быстрее, компактнее, тише, дешевле и потребляют гораздо меньше энергии. Для построения 8-битного сумматора по-прежнему требуются 144 транзистора (или больше, если вы хотите заменить сквозной перенос схемой ускоренного переноса), однако при этом размер схемы микроскопический.