Чарльз Петцольд - Код. Тайный язык информатики

Убедившись в том, что реле действительно можно соединить для сложения двоичных чисел, зададимся вопросом: «А как насчет вычитания?» Не бойтесь показаться смешным, задавая его. На самом деле вы довольно проницательны. Сложение и вычитание в некотором смысле дополняют друг друга, однако механика у этих операций разная. Сложение предполагает последовательное продвижение от крайнего правого столбца цифр до крайнего левого. Каждое значение, перенесенное из одного столбца, прибавляется к следующему. При вычитании мы ничего не переносим ; мы заимствуем , а это действие предполагает использование довольно запутанного механизма.

Давайте рассмотрим типичную задачу на вычитание с заимствованием.

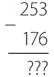
Начнем решение с крайнего правого столбца. Сначала мы замечаем, что 6 больше 3, поэтому нам нужно занять 1 у 5, а затем вычесть 6 из 13, в результате чего получается 7. Мы помним, что заняли 1 у 5, поэтому вместо 5 имеем 4, что меньше 7, поэтому занимаем 1 у 2, вычитаем 7 из 14 и получаем 7. Мы заняли 1 у 2, поэтому у нас есть только единица, из которой вычитаем 1 и получаем 0. Наш ответ — 77.

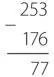
Как же заставить группу логических вентилей следовать такой странной логике?

Не будем даже пытаться. Вместо этого используем небольшой трюк, позволяющий вычитать без заимствования. Это порадовало бы Полония («Не занимай и не ссужай») и всех остальных. Кроме того, подробное рассмотрение процесса вычитания полезно, поскольку напрямую связано с использованием двоичных кодов для хранения в компьютерах отрицательных чисел.

Числа, участвующие в операции вычитания, называются уменьшаемым и вычитаемым . Вычитаемое вычитается из уменьшаемого, результатом является разность .

Чтобы произвести вычитание без заимствования, сначала нужно вычесть вычитаемое из 999, а не из уменьшаемого.

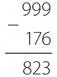
В данном случае используем число 999, поскольку числа, участвующие в операции, состоят из трех цифр. Если бы они были четырехзначными, мы бы использовали число 9999. При вычитании числа из строки девяток получаем число, называемое дополнением до девяти . Дополнение числа 176 до девяти — 823. Это работает и в обратную сторону: дополнение числа 823 до девяти — 176. Вся прелесть в том, что вне зависимости от значения вычитаемого вычисление его дополнения до девяти никогда не требует заимствования .

После вычисления дополнения вычитаемого до девяти нужно прибавить к нему исходное уменьшаемое.

Наконец, прибавить 1 и вычесть 1000.

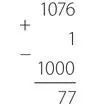
Вот и всё. Мы получили такой же результат, как и раньше, ни разу не прибегнув к заимствованию.

Почему это работает? Исходная задача на вычитание такова:

253 – 176.

Если к этому выражению прибавить и вычесть любое число, результат останется прежним. Так что давайте прибавим и вычтем 1000:

253 – 176 + 1000 – 1000.

Выражение эквивалентно следующему:

253 – 176 + 999 + 1 – 1000.

Теперь числа можно перегруппировать:

253 + (999 – 176) + 1 – 1000.

Это соответствует вычислению, которое я продемонстрировал с использованием дополнения до девяти. Мы заменили одно вычитание двумя вычитаниями и двумя сложениями, избавившись при этом от всех нежелательных заимствований.

А если вычитаемое больше уменьшаемого? Рассмотрим такой пример.

Обычно вы смотрите на подобную задачу и думаете: «Хм, вычитаемое больше уменьшаемого, поэтому придется поменять числа местами, выполнить вычитание и не забыть о том, что результат будет отрицательным». Вы можете произвести перестановку чисел в голове и записать ответ следующим образом.

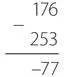
Процесс выполнения данного расчета без заимствований несколько отличается от предыдущего примера. Как и раньше, мы начинаем с вычитания вычитаемого (253) из 999 для получения дополнения до девяти.

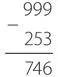
Теперь прибавим дополнение до девяти к исходному уменьшаемому.

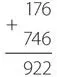
На этом этапе в более раннем примере для получения окончательного результата мы могли прибавить 1 и вычесть 1000. Однако в данном случае эта стратегия не сработала бы, поскольку нам пришлось бы вычесть 1000 из 923, что в действительности потребовало бы вычесть 923 из 1000, и без заимствований мы бы не обошлись.

Вместо этого, по аналогии с прибавлением 999, вычтем 999.

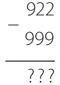
Сразу становится очевидным, что наш ответ будет отрицательным, поэтому следует поменять числа местами и вычесть 922 из 999. Это опять же не требует заимствований, а ответ совпадает с ожидаемым.

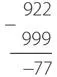
Этот метод применим и к двоичным числам, работать с которыми оказывается проще, чем с десятичными. Давайте посмотрим, как это работает.

Вот исходная задача на вычитание.

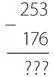
После преобразования чисел в двоичные получаем следующую задачу.

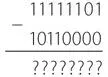
Шаг 1. Вычесть вычитаемое из 11111111 (что соответствует 255).

При работе с десятичными числами вычитаемое вычиталось из строки девяток, а результат назывался дополнением до девяти. При работе с двоичными числами вычитаемое вычитается из строки единиц, результат — дополнение до единицы . Заметьте, что нам на самом деле не нужно выполнять вычитание, чтобы вычислить дополнение до единицы, поскольку каждый 0 в исходном числе превращается в 1 в дополнении до единицы, а каждая 1 превращается в 0. По этой причине дополнение до единицы иногда также называется отрицанием или инверсией . (Сейчас вы, вероятно, вспомнили о том, что в главе 11 мы конструировали устройство, называемое инвертором, которое меняло 0 на 1, а 1 на 0.)