Олег Власов - Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния

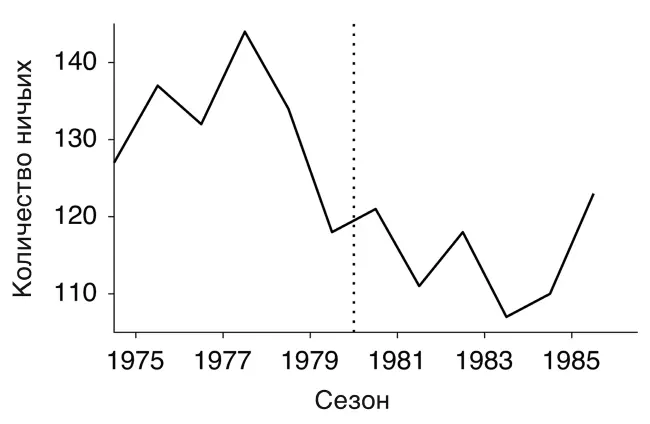
Рисунок 6.1. Количество ничьих в Первом дивизионе до и после перехода на трехочковую систему. Пунктиром обозначен год (1980), когда изменение было реализовано.

Но двух сезонов недостаточно для корректного статистического сравнения. На рисунке 6.1 приведен график количества ничьих в шести сезонах Первого дивизиона до изменения и шести сезонах после этого. Теперь мы видим, что в сезоне-1980/81 было крайне мало ничьих в сравнении с другими сезонами до перехода. До изменения мы видим пять сезонов с наибольшим количеством ничьих; четыре сезона с наименьшим количеством ничьих приходятся на период после перехода. Такого объема данных достаточно для статистической проверки и поддержки заключения, что решение перейти на трехочковую систему поощряло атакующий футбол [61] Я провожу критерий суммы рангов с нулевой гипотезой, что нет разницы между количеством ничьих до и после изменения до трех очков. Значение р равно 0,0108. . Если бы на графике мы представили голы за игру для тех же сезонов, мы обнаружили бы небольшой рост после введения системы трех очков за победу. Мы должны отдать ему должное: Джимми Хилл был прав. Он разрушил футбольный порядок.

В моей выдуманной гипотетической встрече между вашей скромной командой и «Арсеналом» Венгера я допустил немало предположений. Вероятности победы, проигрыша или ничьей весьма специфичны – 32 %, 48 % и 20 % соответственно. В реальных условиях мы ожидаем, что эти вероятности будут меняться в зависимости от соперника, матча дома или на выезде, принятой тактики на матч, травмы ведущего нападающего и т. д.

Это разнообразие возможных результатов не является проблемой для математики стратегии. На самом деле красота математики заключается в ее способности делать обобщения. Мы, математики, обычно не работаем со специфическими вероятностями, такими как вероятность победы и проигрыша, – мы пытаемся решать проблемы более обобщенно. Для этого мы заменяем числа символами, которые могут принимать диапазон значений, и мы доказываем результаты в отношениях между символами. Например, я предположил, что при переходе с атакующей модели на оборонительную вероятность вашей победы уменьшится вдвое (с 32 % до 16 %), и шанс на победу «Арсенала» также сократится в два раза – с 48 % до 24 %. Чтобы обобщить модель, мы можем предположить, что оборона уменьшает вероятность победы или поражения на относительное число, которое мы можем назвать p . Символ p можно представить как отображающий эффективность защиты: p = 1 – это бесполезная защита, p = 0 – отображает железный занавес. В предыдущем примере я установил p = 0,5 – ровно посередине между двумя крайностями.

Я также могу заменить вероятность победы, проигрыша и ничейного результата соответствующими символами: w, l и d . Это позволяет мне создать очень общее представление о футбольном матче, где любой результат возможен. Вопрос в том, как вероятность различных результатов, а также эффективность защиты команды влияет на тактические решения тренеров.

Обозначив задачу через w, l, d и p и используя алгебру, я обнаружил, что при системе начисления двух очков за победу слабая команда должна всегда обороняться [62] Предположим, что если обе команды атакуют, тогда вероятность выигрыша вашей команды равна w , ничьей d , а поражения – l . Если одна из команд защищается, то вероятность победы или поражения умножается на p – эффективность защиты. Это дает следующие вероятности выигрыша, розыгрыша и проигрыша: pw, d + ( 1 – p ) w + ( 1 – p ) l, pl . В x -очковой системе слабая команда должна защищаться, если ( 1 – p ) w + ( 1 – p ) l > > xw ( 1 – p ), то есть l > ( x – 1 ) w . В системе двух очков за победу х = 2, то есть l > w . Слабая команда всегда должна обороняться. При х = 3 условие l > 2 w . Таким образом, слабая команда должна защищаться только в том случае, если вероятность поражения при атаке в два раза выше, чем при обороне. . Если у вашего оппонента больше шансов победить, чем у вас (то есть l > w ), то всегда лучше защищаться. Мы снова видим строгую иерархию, в которой более сильные команды атакуют, а слабые команды защищаются.

В системе с тремя очками за победу результат совершенно другой. Здесь вы должны атаковать, если вероятность поражения соперника не более чем вдвое превышает шансы на вашу победу (то есть когда l < 2w). С другой стороны, если шансы оппонента на победу в два раза больше ваших, вам следует обороняться. В трехочковой системе мы видим множество ситуаций, когда более слабые команды должны играть в атакующий футбол.

С точки зрения математической изощренности переход на символы является продвижением вперед по сравнению с просто числами. Сделав этот шаг, теперь я могу дать очень общий совет тренерам, чьи команды борются за три очка: «Атакуйте, если шансы соперника на победу превышают ваши не более чем вдвое». Этот совет применяется независимо от того, противостоит вам «Арсенал» или «Аккрингтон Стэнли». Вы должны оценить силу собственной команды и оппозиции. Пока шансы на победу оппонента не превышают ваши собственные больше чем в два раза, нацельтесь на максимальный результат и никогда не играйте на ничью. При любой возможности вы должны быть нацелены на результат.

Этот стратегический совет по-прежнему оставляет много работы для тренера. Он должен быть уверен, что знает относительные силы своей команды и соперника. Одним из видов измерения может стать сравнение букмекерских ставок. Второй можно найти, изучив таблицу и сравнив количество побед. В сезоне-2013/14 Премьер-лиги команды из середины таблицы (такие, как «Кристал Пэлас», «Ньюкасл» и «Сток Сити») выиграли примерно половину матчей с лидерами – «Ливерпулем», «Челси» и «Манчестер Сити», например. Таким образом, команды из середины должны не избирать защитную стратегию в играх с лучшими командами, а пытаться бороться за результат. С другой стороны, команды-борцы за выживание должны атаковать в матчах против соперников из середины таблицы; но когда Венгер или Юрген Клопп приезжают в гости со своими суперзвездами, они должны закрыть штрафную площадь на замок и надеяться на ничью.

Из статистики мы знаем, что футбол стал более атакующим после введения новой системы начисления очков в 1981 году. Но действительно ли тренеры производили расчеты? Делали ли они все вычисления, как и я, в ходе которых выяснили, что должны атаковать даже при вдвое меньших шансах на победу? Вряд ли так было. Футбольные тренеры, безусловно, талантливые личности. Они должны справляться с игроками, болельщиками и председателями клуба, а также обладать интуицией и пониманием игры, как и организационными навыками. Также будет полезным некоторое логическое мышление о тактике, но манипулирование математическими символами – это не то, что мы ожидаем увидеть в списке навыков каждого тренера. Тем не менее, похоже, они реагировали на изменения в стимулах именно так, как предсказывает математика. Итак, как же тренеры решили проблему Атака/Защита?