Александр Селюцкий - Вдохновение по заказу. Уроки изобретательства

ПРЕДСТАВЬТЕ СЕБЕ

Третья (аналитическая) стадия алгоритма состоит из восьми шагов. Большинство задач решается именно на третьей стадии, но здесь приходится преодолевать целый ряд психологических барьеров.

Вернемся к задаче о регулировании поперечного сечения трубопровода, по которому течет пульпа с частицами железной руды. Условия задачи мы тогда изложили так: «Дан жидко-степровод с регулятором сечения, по жидкостепроводу движется вода с частицами железной руды. Частицы руды истирают регулятор».

Сформулируем для зтой задачи идеальный конечный результат (ИКР) исходя из правил шага 3—1:

а) объект — жидкостепровод;

б) что делает? — меняет свое сечение;

в) как делает? — сам;

г) когда делает? — когда надо регулировать поток;

д) при каких обязательных условиях? — не истираясь.

Далее требования алгоритма звучат так:

3—2. Второй шаг. Сделаем два рисунка: «было» (до ИКР) и «стало» (ИКР).

Примечания: 1. Рисунки могут быть условными — лишь бы они отражали суть «было» и «стало». 2. Рисунок «стало» должен совпадать со словесной формулировкой ИКР.

Проверка: на рисунках должны быть все элементы, перечисленные в 2—За. Если при шаге 2—5 выбрана внешняя среда, ее надо указать на рисунке «стало».

3—3. Третий шаг. На рисунке «стало» найти элемент, указанный в 3—1а, и выделить ту его часть, которая не может совершить требуемого действия при требуемых условиях. Отметить эту часть (штриховкой, другим цветом, обводкой контуров и т. п.).

3—4. Четвертый шаг. Почему эта часть сама не может осуществить требуемое действие?

Вспомогательные вопросы:

а) чего мы хотим от выделенной части объекта?

б) что мешает выделенной части самой осуществить требуемое действие?

в) в чем несоответствие между «а» и «б»?

3—5. Пятый шаг. При каких условиях эта часть сможет осуществить требуемое действие (какими свойствами она должна обладать)?

Примечание: не надо пока думать, осуществимо ли практически желаемое свойство. Назовите это свойство, не беспокоясь о том, как оно будет достигнуто.

3-6. Шест ой шаг. Что надо сделать, чтобы выделенная часть объекта приобрела свойства, отмеченные в 3—5?

Вспомогательные вопросы:

а) покажите на рисунке стрелками силы, которые должны быть приложены к выделенной части объекта, чтобы обеспечить желательные свойства;

б) какими способами можно создать эти силы? (вычеркнуть способы, нарушающие условия 3—1д).

3—7. Седьмой шаг. Сформулировать способ, который может быть практически осуществлен. Если таких способов несколько, обозначьте их цифрами (самый перспективный цифрой 1 и т. д.). Запишите выбранные способы.

3—8. Восьмой шаг. Дать схему устройства для осуществления первого способа.

Вспомогательные вопросы:

а) каково агрегатное состояние рабочей части устройства?

б) как меняется устройство в течение одного рабочего цикла?

в) как меняется устройство после многих циклов?

(После решения задачи следует вернуться к шагу 3—7 и рассмотреть другие перечисленные в нем способы.)

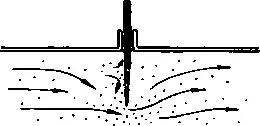
СТАЛО

БЫЛО

Проследим теперь ход решения этой задачи на протяжении всей третьей стадии.

Шаг 3—2. Делаем два рисунка: «было» и «стало».

Шаг 3—3. В нашем случае частью жидкостепровода, которая не может совершить требуемого действия (менять своего сечения)

при требуемых условиях (когда надо регулировать поток и притом без истирания), будет внутренняя поверхность жидкостепро-вода.

Шаг 3—4. а) мы хотим, чтобы внутренняя поверхность трубы сама меняла сечение потока;

б) однако внутренняя часть трубы неподвижна и не может оторваться от стенок трубы;

в) несоответствие именно в том и состоит, что внутренняя поверхность грубы в одно и то же время должна быть неподвижной (как элемент жесткой трубы) и подвижной (как сжимающийся и разжимающийся элемент регулятора).

Шаг 3—5. Теперь очень важно суметь сформулировать свойства, которыми должен обладать наш объект, чтобы он мог выполнять свою задачу. Для нашей задачи это можно выразить так:

«На внутренней поверхности жидкостеировода появляется какой-то слой вещества, тем самым внутренняя поверхность переносится ближе 1к оси трубы. При необходимости этот слой уменьшается или исчезает, и внутренняя поверхность отдаляется от оси трубы».

Шаг 3—6. Так что же сделать с жидкостенроводом, чтобы его внутренняя поверхность приобрела эти свойства (сужение и расширение) ?

а) эти силы должны быть приложены к выделенной части объекта, чтобы обеспечить желательные свойства;

б) вот он, момент «озарения»! А посмотрите, как нрозаическр1 он выглядит, если не нарушать логику рассуждений. Внутри жид-костепровода, по условиям задачи, движется вода с частицами железной руды. Значит, наращивать на внутреннюю поверхность трубы мы и можем либо воду (разумеется, «наращивать» воду можно только в том случае, если она находится в твердом состоянии — в виде льда), либо частицы железной руды.

Шаг 3—7. Поскольку быстрое замораживание воды — дело сложное, гораздо проще осуществить «наращивание» стенкп жиД-костепровода за счет частиц железной руды: ведь они обладают магнитными свойствами.

Итак, для того, чтобы иметь неистирающуюся задвижку, надо выполнить участок трубы из немагнитного материала и при помощи электромагнитного поля «наращивать» на внутренюю поверхность жидкостепровода частицы руды.

Шаг 3—8. Теперь ясно, что а) агрегатное состояние рабочей части нашего устройства — жидкое;

б) в течение одного рабочего цикла агрегатное состояние устройства меняется, переходя из жидкости (точнее,— суспензии) в твердое тело;

в) практически наше устройство «вечно»: оно совершенно не меняется при неограниченном количестве рабочих циклов.

Мы последовательно рассмотрели ход решения одной задачи. Но не всегда нам надо добиваться «озарения», осуществляя все восемь шагов третьей части АРИЗ. Очень важную роль в процессе решения играет шаг 3—2. Даже -если нам кажется, что мы

■очень удачно сформулировали идеальный конечный результат (ИКР), все равно обязательно надо сделать рисунки. Насколько рисунок может помочь решению задачи, можно убедиться на следующем примере.

Представьте себе, что вам необходимо повысить дальность пробега самоходного шасси (самоходное шасси представляет собой