Микаэль Лонэ - Большой роман о математике. История мира через призму математики

Очень часто во время моих выступлений я слышу вопрос, почему мне так нравится математика. «Как вы пришли к этому странному увлечению? – часто спрашивают меня. – Вам привил любовь к этому предмету какой-то конкретный учитель? Вы заинтересовались математикой уже тогда, когда были ребенком?» Любовь к этому предмету не перестает удивлять людей, которые раньше математикой не интересовались.

Признаться, я даже не знаю, что же это было конкретно. Насколько помню, я всегда любил математику, и я не могу назвать конкретное событие в моей жизни, которое привело меня к этому. Тем не менее, если задуматься, начинаю припоминать свое восторженное состояние, когда узнавал о чем-то новом. Так, например, было, когда я столкнулся с умножением.

Мне исполнилось 9 или 10 лет, когда, держа в руках свой калькулятор, я нажал на несколько клавиш и получил следующий результат: 10 × 0,5 = 5. Умножив число 10 на 0,5, я получил 5 – такой результат предоставил мне мой калькулятор, которому я полностью доверял и считал, что сомневаться в его результатах неразумно. Как путем умножения числа может получиться меньшее число? Разве умножение не предполагает увеличение? Не противоречит ли это самому значению слова «умножить»? Мой дорогой калькулятор, не лучше ли тебе будет пересчитать результат и предоставить число, большее, чем 10?

Мне потребовалось несколько недель, чтобы все переосмыслить и прояснить, почему получается именно такой результат. В конечном счете я рассмотрел данный вопрос с геометрической точки зрения, подобно тому, как это делали древние мыслители. Возьмем прямоугольник, длина которого составляет 10 единиц, а ширина 0,5. Его площадь соответствует площади пяти небольших квадратов со стороной 1.

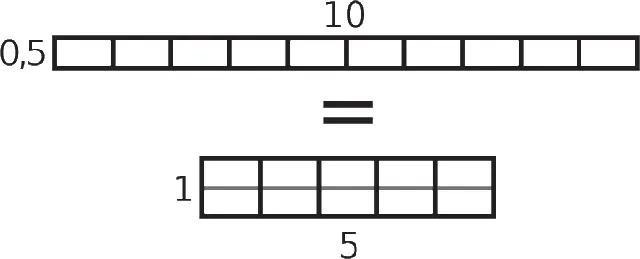
Другими словами, умножение на 0,5 есть не что иное, как деление на 2. Аналогичное действие можно применить и к другим числам: умножить на 0,25 значит разделить на 4, умножить на 0,1 – разделить на 10 и так далее.

Объяснение убедительно, однако его вывод обескураживает: слово «умножение» в математике не полностью соответствует своему обычному значению. Кому придет в голову утверждать, что площадь сада умножена после продажи половины? Или кто станет утверждать, что его богатство умножается после потери его 50 %? В таком случае преумножить хлеба чудесным образом сможет каждый: просто съешьте половину, и вуаля.

Обнаружив этот феномен в первый раз и сделав вывод, я был сильно впечатлен. Игра слов рождает особые чувства и эмоции. В любом случае эффект, произведенный на меня в детстве этим открытием, был очень силен. Спустя много лет я читал книгу математика Анри Пуанкаре «Наука и метод», опубликованную в 1908 году, и нашел следующее предложение: «Математика – это искусство давать одно и то же имя разным вещам». Это лучшая характеристика явления, с которым я однажды столкнулся.

Стоит признать, что этот тезис, вероятно, может быть применен к любому языку. Под словом «плод», например, могут пониматься яблоки, вишни или помидоры. Каждый вид плода, в свою очередь, имеет множество различных сортов, которые и дальше могут подразделяться на подвиды в целях анализа их свойств. Однако Пуанкаре справедливо отмечает, что ни один другой язык не зашел так далеко в своих обобщениях, как математика. Для математиков умножение и деление – это, по сути, одна и та же операция. Умножение на число может быть представлено как деление на другое число. Все зависит от того, с какой точки зрения посмотреть на данный вопрос.

Введение понятия «ноль» и отрицательных чисел также не может не волновать ум. Чтобы открыть эти числа, нам было бы необходимо набраться храбрости и пойти против своего собственного языка, перестроиться и осознать, что в языке возможны различные значения. Индийские ученые стали первыми, кто осмелился на такой шаг.

Если я скажу вам, что уже несколько раз был на Марсе или несколько раз встречался с Брахмагуптой лично, поверите ли вы мне? Скорее всего, нет. И вы будете правы, потому что, по правилам нашего языка, эти предложения означают, что я на самом деле уже был на Марсе и встречался с Брахмагуптой. Но если задуматься над этими утверждениями с точки зрения математики, просто скажем, что я был на Марсе и встречался с Брахмагуптой ноль раз – таким образом, я говорил правду. В общении принято использовать различные структуры фразы для утвердительных предложений: «Я был на Марсе» – и отрицательных: «Я не был на Марсе». С точки зрения математики, построение фразы будет однотипным: во фразе: «Я был на Марсе несколько раз» под словом «несколько» может пониматься в том числе ноль.

В то время как несколько веков назад древние греки с большим трудом приняли 1 в качестве числа, представьте себе, какую революцию произвело применение понятия «число» к пустоте. До ученых из Индии некоторые люди уже пытались рассуждать об этом, но никто не смог до конца сформулировать свои рассуждения. В Месопотамии, начиная с III в., встречается упоминание о цифре 0. Ранее в их системе исчисления уже использовалась эта цифра для добавления разрядов, например 25 и 250. Использование в написании чисел цифры 0 добавляло больше неясности. Кроме того, вавилоняне никогда не использовали отдельно написанную цифру 0 для обозначения полного отсутствия чего-либо.

На другом конце света майя также начали использовать ноль. Они даже придумали два их вида! Первый, как и вавилоняне, они использовали для обозначения разрядов в двадцатичной системе исчисления. Второй же использовался не как число, а как название дня в календаре. В каждом месяце в календаре майя было двадцать дней, пронумерованных от 0 до 19. Ноль записывали отдельно от других символов, однако его применение не носило математического характера. Майя никогда не использовали отдельно написанный 0 для выполнения арифметических операций.

Таким образом, Брахмагупта был первым, кто в полной мере описал ноль как самостоятельное число и его свойства: при вычитании из числа равного ему получается ноль; при сложении нуля с числом или вычитании из числа нуля получится это же число. Описанные арифметические свойства кажутся нам очевидными, но тот факт, что они так последовательно описаны в работе Брахмагупты, говорит о том, что ноль становится полноценным числом наряду со всеми остальными. Описание свойств числа 0 способствовало появлению отрицательных чисел. Тем не менее пройдет еще много времени, прежде чем математики начнут использовать их в своих исследованиях.

Китайские ученые были первыми, кто описал величины, которые могут быть соотнесены с отрицательными числами. В своих комментариях к «Математике в девяти книгах» Лю Хуэй рассказывает о системе цветных палочек для представления положительных и отрицательных значений. Красная палочка обозначает положительное число, черная – отрицательное. Лю Хуэй подробно объясняет, как эти два вида чисел взаимодействуют друг с другом, в том числе как они складываются или вычитаются.