Микаэль Лонэ - Большой роман о математике. История мира через призму математики

Расположенный в Гранаде (Андалусия) дворец Альгамбра является одним из самых значительных памятников исламского искусства эпохи Средневековья, расположенных в Испании. Более двух миллионов туристов посещают его ежегодно. Мало кто из них догадывается, что дворец пользуется особой репутацией среди математиков. Альгамбра знаменита тем, что в ее оформлении использованы все семнадцать способов замощения, которые распределены (а иногда хорошо спрятаны) в залах и садах. Так что, если вам когда-нибудь посчастливится провести день в Гранаде, вы знаете, что делать.

Останемся еще ненадолго в Багдаде и попытаемся выяснить, что же на самом деле происходит за дверями Байт аль-Хикмы. Какие новые открытия сделали арабские математики? О чем все эти книги, что лежат на полках библиотеки?

Одна из новых дисциплин, развивающихся активно в этот период, получила название тригонометрия и занималась изучением величин треугольников. На первый взгляд, это может разочаровать, т. к. древние народы уже изучали треугольники, подтверждением чего является теорема Пифагора. Арабские ученые пошли дальше в своих исследованиях и достигли удивительно точных результатов, которые активно используются и сегодня.

Вопреки кажущейся простоте не все свойства треугольников так очевидны, и ряд из них еще уточнят в конце эпохи Античности. Треугольник определяется шестью своими основными свойствами: длины трех его сторон, а также величины трех его углов.

Например, для того, чтобы измерить расстояние между двумя точками с использованием тригонометрии, достаточно просто найти угол между ними, чтобы избежать необходимости непосредственного измерения этого расстояния. Для астрономии это особенно актуально. Рассчитать расстояния между звездами, которые мы наблюдаем в ночном небе, очень сложно, и может потребоваться несколько столетий, чтобы найти ответ. А вот измерить угол между этими звездами или углы, образуемые с горизонтом, гораздо проще. Обычного октанта, [9]которому на смену пришел секстант, [10]вполне хватит для этой задачи. Аналогично этому, географу для составления карты достаточно измерить углы треугольника, образованного тремя вершинами гор. Для этого ему потребуется только алидада – прибор, представляющий собой не что иное, как транспортер, на концах которого прикреплено визирное устройство. А для того чтобы сориентировать карту в пространстве, можно использовать лишь компас, с помощью которого измеряют угол между севером и заданным направлением. Непосредственное же измерение расстояний между тремя горами требует организации соответствующей экспедиции и проведения значительно более сложных вычислений. Пример Александра Македонского и его бематистов подтверждает возможность реализации и такого проекта!

Таким образом, задача заключается в следующем: как узнать все данные о треугольнике и при этом сделать минимум измерений? Задаваясь этим вопросом, теоретики тригонометрии столкнулись с проблемой, аналогичной той, которая стояла перед Архимедом тысячелетием ранее. Во-первых, если вам известны размеры всех углов треугольника, но не известен размер ни одной из его сторон, можно сделать вывод, что вам известна его форма, но не размер. Для наглядности ниже продемонстрированы примеры таких треугольников, имеющих равные углы, но различную длину соответствующих сторон.

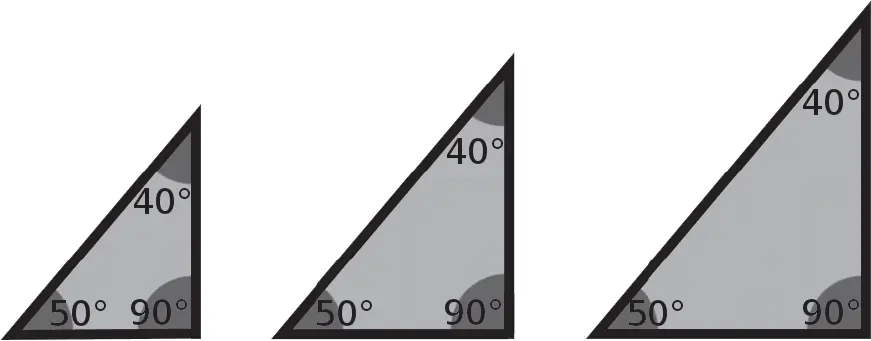
Тем не менее все они имеют одинаковые пропорции. Например, если необходимо определить, на какое число надо умножить длину самой длинной стороны, чтобы определить длину самой короткой, то можно выяснить что для каждого из этих трех треугольников результат будет одинаковый: 0,64! Аналогично тому, как в случае с определением периметра окружности необходимо умножить его диаметр на π, независимо от его размера.

Если быть совсем точным… почти 0,64 – это приблизительное число. Что касается π, эта величина не может быть вычислена точно, и нам приходится довольствоваться ее приблизительным значением. Можно попытаться определить значение более точно, как 0,642 или даже 0,64278, но это все еще далеко от совершенства. Десятичное значение этого числа имеет бесконечное число знаков после запятой. Аналогичным образом дело обстоит со всеми величинами, которые могут быть вычислены в этих треугольниках. Так, чтобы рассчитать величину средней стороны треугольника, необходимо умножить величину самой длинной стороны на 0,766, а чтобы рассчитать величину длинной стороны треугольника, необходимо умножить величину короткой стороны на 1,192.

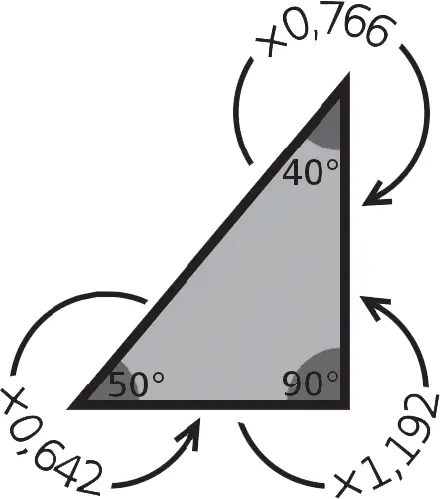
Так как невозможно определить точные значения этих трех соотношений, математики дали им свои имена, для того чтобы обозначить предмет своего изучения. В ходе исторического развития они именовались по-разному, но сегодня общепринято называть их косинус, синус и тангенс соответственно. Различные варианты были введены и использовались, прежде чем были преданы забвению. Так, например, произошло с величиной секед, которую древние египтяне использовали для измерения наклона пирамид. В качестве еще одного примера такой величины можно назвать хорду равнобедренного треугольника, которую описали в Древней Греции.

Определение тригонометрических соотношений осложняется еще одним обстоятельством: их значения в различных треугольниках отличаются. Так, значения 0,642, 0,766 и 1,192 действительны только для треугольников с углами 40°, 50° и 90°. Если же взять прямоугольный треугольник с углами 20°, 70° и 90°, то значения косинуса, синуса и тангенса будет приблизительно равны 0,342, 0,940 и 2,747 соответственно! Таким образом, исследования в области тригонометрии потребовали гораздо больших усилий, чем ожидалось. Речь шла о поиске не только одного значения или даже трех, а о целых таблицах чисел, которые отличаются в зависимости от размера углов!

Ниже представлена таблица с тригонометрическими величинами для треугольников, один угол которых находится в диапазоне от 10° до 80°. Обратите внимание на то, что для каждого треугольника указан только один угол. Указывать значение других углов не имеет смысла, т. к. второй угол всегда составляет 90°, а третий определяется согласно описанной ранее теореме, с помощью вычитания из 180° суммы двух других заданных углов. Таким образом, даже не имеет смысла рисовать треугольники: значения одного угла достаточно. Поэтому в первом столбце тригонометрических таблиц, как правило, указывается только один угол. Так, косинус 10° равен 0,9848, а тангенс 50° составляет 1,1918.