Микаэль Лонэ - Большой роман о математике. История мира через призму математики

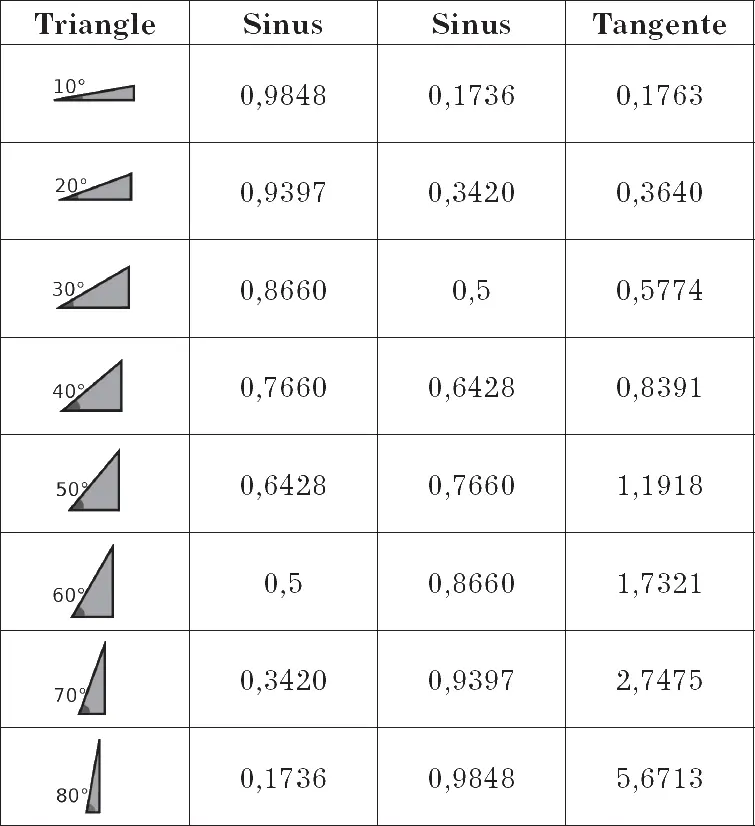
Конечно же, представленная таблица не является полной. Всегда можно продолжить ее, указав более точные значения тригонометрических величин либо добавив значений для углов, не представленных в текущей редакции. В этой таблице перечислены треугольники с углами в диапазоне от 10° до 80°, но было бы лучше указать точные значения для всех возможных углов, вплоть до десятых градуса. Уточнять тригонометрические таблицы можно было до бесконечности, чем последовательно занимались математики. Так было вплоть до XX в., когда изобрели калькуляторы, что существенно упростило расчеты.

Древние греки, вероятно, стали первыми, кто начал составлять тригонометрические таблицы. Самое раннее сохранившееся свидетельство – «Альмагест» Птолемея, в котором содержатся исследования Гиппарха Никейского – математика, жившего во II в. до н. э. В конце V в. н. э. индийский ученый Ариабхата также опубликовал свои тригонометрические таблицы. В Средние века в Персии Омар Хайям в XI в. и аль-Каши в XIV в. также составили одни из наиболее известных тригонометрических таблиц своего времени.

Ученые арабского мира продвинутся дальше всех не только в составлении наиболее точных таблиц, но и научатся эффективно применять на практике полученные данные.

Аль-Каши опубликовал в 1427 г. книгу под названием «Мифтах аль-Хисаб», или «Ключ к арифметике», в котором приводит результат, обобщающий теорему Пифагора. Благодаря расчетам косинуса аль-Каши удается применить эту теорему не только к прямоугольным треугольникам, но и к любым другим. Теорема аль-Каши работает, дополняя теорему Пифагора: если треугольник не прямоугольный, то сумма квадратов катетов не равна квадрату гипотенузы. Однако это равенство будет верным при условии добавления корректирующего коэффициента, который рассчитывается непосредственно из косинуса угла, образуемого этими двумя сторонами.

Когда аль-Каши опубликовал эту работу, он уже был известным математиком. Прославился он тремя годами ранее после вычисления приближенного значения числа π до шестого знака после запятой – максимально точное значение для той эпохи! В то время как рекорды могут быть побиты, [11]теоремы сохраняют свою силу вне зависимости от времени. Теорема аль-Каши и по сей день остается одной из самых важных в области тригонометрии.

Перенесемся на левый берег Парижа. На дворе стоит июнь, и я, можно сказать, выступаю в роли экскурсовода. Сегодня с группой, состоящей человек из двадцати, я прогуливаюсь по улицам Латинского квартала по следам исторического развития математики. Наша следующая остановка будет в Саду великих исследователей. В северной его части расположены симметричные аллеи Люксембургского сада, массивными рядами ведущие ко дворцу Сената. В южной части возвышается купол Парижской обсерватории.

Следуя по центральной дорожке сада, мы, словно по канату, идем по линии меридиана Парижа. Шаг влево, и мы оказываемся в восточном полушарии мира. Два шага вправо – и мы уже в Западном полушарии. Еще через пятьсот метров меридиан пересекает обсерваторию, тянется посередине 14-го округа Парижа, а затем выходит через парк Монсури. Далее он уходит за пределы города, частично проходит по территории Испании и устремляется через Африканский континент и Антарктический океан к Южному полюсу. С другой стороны он идет по улицам Монмартра, слегка соприкасается с Британскими островами и Норвегией, а затем устремляется к Северному полюсу.

Начертить линию меридиана было не так-то просто. Это требовало точных измерений колоссального масштаба. Как, например, узнать расстояние между двумя точками по разные стороны горы, не пересекая ее при этом? Для того чтобы ответить на этот вопрос, ученые в начале XVIII в. разметили траекторию меридиана, мысленно покрыв всю территорию Франции с севера на юг сеткой из треугольников.

В качестве точек триангуляции выбрали наиболее высокие географические объекты, такие как холмы, горы или башни, откуда можно было увидеть другие точки для измерения углов между ними. После проведения измерений на земле можно было в полной мере использовать тригонометрические методы, разработанные арабами, чтобы определить точное положение каждой точки триангуляции, а затем провести через них меридиан.

Одним из первых эту задачу будет решать Кассини. Род Кассини – это целая династия ученых, которых принято нумеровать, как царей! Джованни Доменико, именуемый Кассини I, только что эмигрировавший из Италии, был первым директором Парижской обсерватории с момента ее основания в 1671 г. После смерти Джованни Доменико в 1712 г. его преемником стал сын Жак, или Кассини II. Именно он в 1718 г. первым провел меридианы с помощью триангуляции. После этого Кассини III (Сезар-Франсуа, сын Кассини II) впервые полностью завершил триангуляцию всей территории Франции. Результатом его работы стала публикация в 1744 г. первой карты Франции, составленной полностью в соответствии с требуемой методикой. Сын Сезара Франсуа, Кассини IV, Жан-Доминик, продолжил эту работу и проводил триангуляцию одного региона за другим.

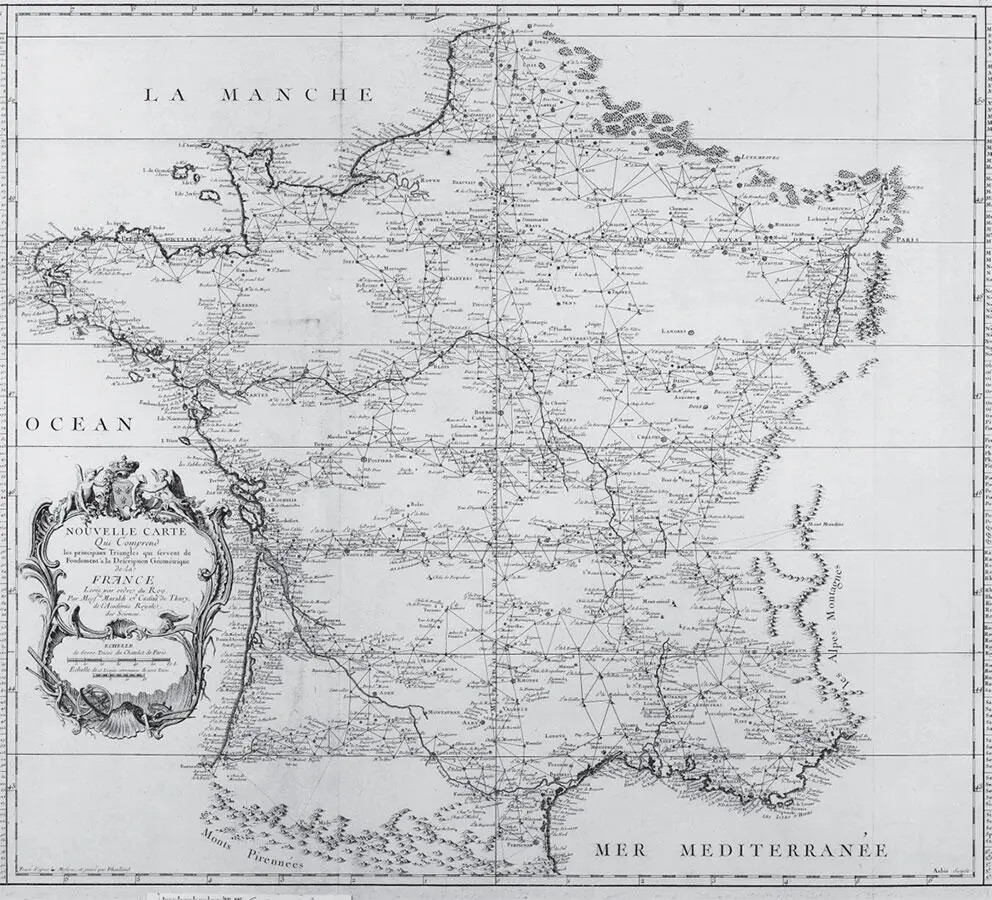
Карта Франции 1744: представлен меридиан, на котором находится Париж, и основные треугольники Кассини

Следуя по меридиану, мы практически идем по стопам арабских ученых, которые создали теоретическую основу для триангуляции. Разметка каждого треугольника на карте требует использования косинуса, синуса или тангенса. Все они есть наследие аль-Каши и первых багдадских ученых, занимавшихся тригонометрией. Все эти расчеты, сделанные вручную, потребовали бесчисленного количества часов, проведенных учеными, работавшими с тригонометрическими таблицами в обсерватории.

Расчеты с помощью триангуляции использовались вплоть до конца XX в., пока не появились спутники. Самая крупная сеть треугольников насчитывала до 80 000 точек. Особые знаки, которые отмечали эти точки, все еще можно встретить на всей территории Франции. В Париже вы можете увидеть две точки, через которые проходит ось меридиана: одна находится в южной части города в парке Монсури, другая – на севере, на Монмартре. В 1994 г. тридцать пять памятных знаков в честь астронома Франсуа Араго были установлены по линии меридиана, проходящей по территории Парижа. Один из них находится прямо в Лувре. В следующий раз, когда станете прогуливаться по улицам Парижа, будьте внимательнее, и, вполне возможно, заметите несколько из них.

Во время французской революции произошел переход на метрическую систему измерения и для универсальности длину 1 метра стали рассчитывать исходя из длины меридиана, а именно как одну десятимиллионную часть четверти длины меридиана. В 1796 г. в четырех концах Парижа установили шестнадцатиметровые камни для того, чтобы каждый мог увидеть эталон длины. По сей день два из них все еще можно увидеть: один – на улице Вожирар с видом на Люксембургский сад, другой – на Вандомской площади у входа в Министерство юстиции.