Микаэль Лонэ - Большой роман о математике. История мира через призму математики

Китайский ученый привел весьма подробное их описание, но все равно остается сделать еще один шаг: рассмотреть положительные и отрицательные числа не в виде двух отдельных групп, а как единую последовательность. Конечно, положительные и отрицательные числа не всегда имеют одинаковые свойства, когда необходимо сделать расчеты, но при этом у них есть много сходств. Похожим образом дела обстоят с четными и нечетными числами, которые образуют две отдельные группы чисел с различными арифметическими свойствами, тем не менее составляют единую совокупность чисел.

Как и в случае с цифрой 0, индийские ученые были первыми, кто объединил все числа в последовательность. Это сделал все тот же Брахмагупта, изложивший свое исследование в вышеупомянутой работе «Брахма-спхута-сиддханта». Развивая исследования Лю Хуэя, он разработал правила, с помощью которых можно производить определенные действия с этими числами. Например, он вывел, что сумма двух отрицательных чисел имеет отрицательное значение, например (–3) + (–5) = –8, произведение положительного числа и отрицательного числа будет отрицательным: (–3) × 8 = –24, а произведение двух отрицательных чисел – положительное: (–3) × (–8) = 24. Последнее свойство может показаться противоестественным – сложно будет с ним согласиться. Даже сегодня это правило смущает школьников во всем мире.

Спустя много веков после того как Брахмагупта сделал свое открытие, правила умножения, особенно «минус × минус = плюс», продолжают вызывать сомнение и непонимание. Эти правила, преподававшиеся в школе, стали интересовать не только математиков, но и представителей других профессий. Так, в XIX в. французский писатель Стендаль сам описывал свое недоумение в автобиографическом романе « Жизнь Анри Брюлара ». Автор « Красного и черного » и « Пармской обители » написал следующие строки:

«По своей юношеской простоте, мне казалось, что математика лишена притворства, и я полагал, что это так во всех науках, о которых я слышал. Но каково же было мое разочарование, когда я узнал, что никто не мог объяснить, почему минус на минус дает плюс (– × – = +)? (Это ведь одна из основ науки под названием алгебра.) Еще печальнее было то, что, не разобравшись в этом правиле (которое, вероятно, имеет свое объяснение, т. к. ведет к истине), его пытаются растолковать совершенно непонятными аргументами […] Сегодня я ограничиваюсь тем, что «минус на минус дает плюс» – верно, потому как очевидно, что применение этого правила приводит к безошибочным результатам».

Правило знаков умножения, которое может показаться странным на первый взгляд, обретает смысл, если продемонстрировать его в действии на системе палочек, разработанной китайскими учеными. Например воспользуемся этой системой для изображения прибыли или убытков. Представим, что черная палочка соответствует €5, а серая – это долг в €5, то есть – €5. Так, если у вас есть 10 черных палочек и 5 серых, ваш баланс равен €25.

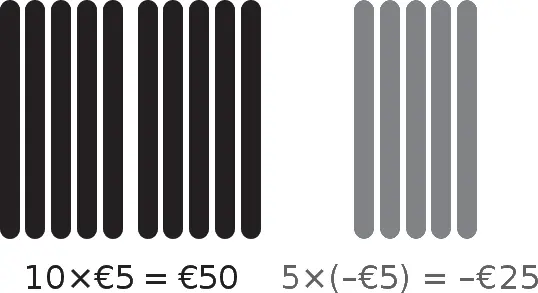
Теперь рассмотрим различные ситуации, которые могут возникнуть, когда ваш счет изменяется. Представьте, что вам дали еще 4 черные палочки: ваш баланс увеличивается на €20. Другими словами: 4 × 5 = 20. Произведение двух положительных чисел положительно, до сих пор все понятно.

Если же теперь вы возьмете 4 серые палочки, то есть четыре долга, ваш баланс уменьшается на €20. Иными словами: 4 × (–5) = –20. Положительное число, умноженное на отрицательное, дает отрицательный результат. И аналогично, если у вас заберут 4 черные палочки, вы теряете €20. То есть (–4) × 5 = –20. Эти две последние ситуации показывают, что приобретение долга может быть представлено как перевод денег. Прибавление отрицательной величины соответствует вычитанию положительной.

Мы подошли к самому важному моменту: что станет с вашим балансом, если у вас заберут 4 серые палочки, – другими словами, если у вас заберут долги? Ответ очевиден: ваш баланс увеличится, т. е. вы получите деньги. И теперь можно наглядно подтвердить, что (–4) × (–5) = 20. Минус на минус дает плюс!

В связи с появлением отрицательных чисел сложение и вычитание перестанут быть такими наглядными. Ситуация очень похожа на умножение на 0,5, что соответствует делению на 2. Так как добавление отрицательного числа соответствует вычитанию положительного, эти две операции утрачивают свое семантическое значение. Прибавление, как правило, ассоциируется с увеличением. Но если прибавить число –3, это означает вычесть 3: например, 20 + (–3) = 17. А вот вычесть (–3) – это значит добавить 3: 20 – (–3) = 23. Еще раз обратим внимание, что одинаковые термины используются для определения различных вещей. С появлением отрицательных чисел сложение и вычитание стали двумя вариантами одной операции.

Эта парадоксальная игра слов, при которой умножение двух меньших чисел дает большее число, препятствовала использованию отрицательных чисел. Долгое время после Брахмагупты многие ученые продолжали быть избирательными в применении этих интересных с практической точки зрения, но сложных для осознания чисел. Некоторые математики называли их «абсурдные числа» и допускали их использование лишь в промежуточных вычислениях, только если в итоге их не будет. В XIX–XX вв. отрицательные числа начали использовать в полной мере. В 711 г. с Востока в долину Инда прибыли две тысячи всадников на конях и верблюдах. Это были войска Мухаммада ибн аль-Касима, молодого арабского командира, которому на тот момент исполнилось всего 20 лет. Обладавшие лучшей подготовкой и оружием, его солдаты победили пятидесятитысячную армию Раджи Даайри и захватили Синд и дельту реки. Для местных жителей это стало трагическим событием, тысячи солдат были обезглавлены, а государство сильно разграблено.

Тем не менее захват Индии молодой арабо-мусульманской империей даст толчок для распространения индийской математики. Арабские ученые дополнили свои исследования индийскими достижениями и распространили их по всему миру. Эхо этих времен отзывается и в математике XXI в.

Перенесемся в 762 г., в Месопотамию, откуда все началось. В то время как Вавилон уже был в руинах, в сотне километров на север шли грандиозные работы. Именно здесь, на правом берегу Тигра, халиф Аббасидов аль-Мансур решил построить новую столицу.

Арабо-мусульманская империя в это время стремительно расширяется. За сто тридцать лет до этого, в 632 г., в то время как Брахмагупта в возрасте 34 лет только что закончил писать свою работу «Брахма-спхута-сиддханта», в Медине умирает пророк Мухаммед. После его смерти халифы распространяют ислам вплоть до юга Испании, реки Инд, на севере Африки, в Персии и Месопотамии.