Микаэль Лонэ - Большой роман о математике. История мира через призму математики

После уравнений второй степени идут уравнения третьей степени. В этот раз неизвестная величина возводится в куб. Эти уравнения еще сложнее для аль-Хорезми – и способ их решения будет сформулирован только в эпоху Ренессанса. С точки зрения геометрии данный вопрос можно изложить в категориях объема и трех измерений.

Далее идут уравнения четвертой степени. С точки зрения чисел сложностей в их решении нет. С геометрической же точки зрения становится затруднительно представить себе фигуры в четырех измерениях, т. к. мы живем в трехмерном пространстве.

Возможности алгебры разрешать проблемы, которые априори недоступны для геометрии, в значительной степени определили сдвиг, который произошел в эпоху Возрождения, в связи с чем пальма первенства в мире математики перешла от геометрии к алгебре.

В конце IX в. египетский математик Абу Камиль стал одним из ведущих преемников аль-Хорезми. Он обобщил методы персидского ученого и особенно уделил внимание системам уравнений. Эти системы предполагали одновременный поиск нескольких неизвестных исходя из нескольких заданных уравнений. Вот классический пример.

Стадо состоит из одногорбых и двугорбых верблюдов. Всего у животных в стаде 100 голов и 130 ног. Сколько животных каждого вида в стаде ?

В данной задаче есть два неизвестных: количество верблюдов одного и другого вида, – и информация о них дана совокупно. Количество голов и горбов позволяют нам составить два уравнения, но их невозможно решить отдельно друг от друга: необходимо объединить их для поиска решения задачи.

Есть несколько методов решения этой задачи. Логика рассуждений следующая. Поскольку в стаде 100 голов, у 100 животных есть хотя бы по одному горбу. Так как в стаде есть только двугорбые и одногорбые верблюды, то у 30 из них будет два горба (130–100), а одногорбыми будут, соответственно, 70 верблюдов (100–30). В данном примере есть только одно правильное решение. В других же системах уравнений их может быть значительно больше. Так, в одном из приводимых примеров Абу Камиль находит 2676 различных решений!

В X в. аль-Караджи был первым, кто написал о том, что можно составить уравнения любой степени, но ему удалось описать решение далеко не всех из них. В XI–XII вв. Омар Хайям и Шарафуддин ат-Туси занимались изучением решения уравнений третьей степени. Им удалось решить отдельные примеры и в целом достичь определенных успехов, но вместе с тем еще не получилось сформулировать обобщенное решение. Некоторые математики также пытались найти решение, и возникло предположение, что, возможно, такие уравнения вообще его не имеют.

В конечном счете ответили на этот вопрос вовсе не арабские ученые. В XIII в., когда золотой век ислама был уже позади, арабская цивилизация начинает постепенно приходить в упадок. Тому было много причин, в частности господство арабской мусульманской империи привлекало внимание завистников, и арабы были вынуждены постоянно обороняться, а на первый план вышли расходы на содержание армии.

В 1219 г. орды монголо-татар под предводительством Чингисхана захватили Хорезм, родной город аль-Хорезми. В 1258 г. они достигли ворот Багдада под командованием хана Хилого, внука Чингисхана. Халиф аль-Мастачит Биллах был вынужден капитулировать. Багдад разграбили и сожгли, а его жителей убили. В это же время идет реконкиста южных территорий Испании. Кордова, столица региона, пала в 1236 г. Испания была полностью завоевана в 1492 г. после захвата Гранады и дворца Альгамбра.

Арабский научный мир был весьма децентрализован, и наиболее важные исследования продолжались вплоть до XVI в., тем не менее центром развития математики отныне стала Европа.

Следует признать, что в эпоху Средневековья математика развивалась в Европе не самыми быстрыми темпами. Тем не менее есть несколько исключений. Наиболее известный европейский математик Средневековья, вероятно, итальянский ученый Леонардо Фибоначчи, родился в Пизе в 1175 г. и умер там же в 1250-м.

Как он сумел стать в это время в Европе известным математиком? Настоящих математиков не осталось на континенте. Отец Фибоначчи был представителем торговцев республики Пиза в Бежайа, на территории современного Алжира. Именно здесь итальянский ученый получил образование и открыл для себя исследования арабских математиков, в том числе аль-Хорезми и Абу Камиля. По возвращении в Пизу он опубликовал в 1202 г. свою работу под названием «Книга абака» («Книга расчетов») , в которой описал все известные ему достижения математики того времени, включая арабские цифры, геометрию Евклида, Диофантову арифметику, расчеты числовых рядов. Один из таких рядов увековечил его имя.

Ряд – это последовательность чисел, которая может быть продолжена бесконечно. Мы уже рассмотрели некоторые из них. Например, нечетные числа (1, 3, 5, 7, 9…) и квадратные числа (1, 3, 9, 16, 25…) – одни из наиболее очевидных. В одной из глав «Книги абака» Фибоначчи пытается математически показать, каким образом будет увеличиваться количество кроликов. Он рассматривал следующие гипотезы в качестве условий:

1) первые два месяца пара кроликов не дает потомства;

2) начиная с третьего месяца пара кроликов дает еще одну пару кроликов.

С учетом этих данных можно построить схему развития пары кроликов, начиная с их рождения.

Каждая линия представляет развитие пары кроликов с течением времени. Стрелочки обозначают рождение новых пар

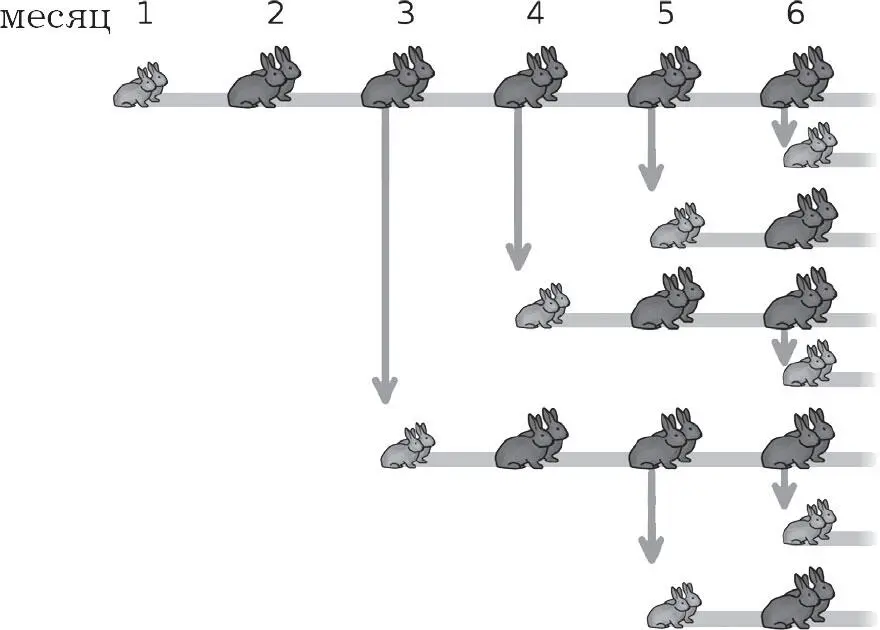
Проанализировав полученный ряд, можно получить числовой ряд. Столбец за столбцом дают следующие значения в первые 10 месяцев: 1, 1, 2, 3, 5, 8…

Фибоначчи обратил внимание на то, что популяция кроликов соответствует сумме популяций в два предыдущих месяца: 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8… и так до бесконечности. Это правило можно объяснить. Каждый месяц число пар, которые родились и прибавились к ранее родившимся кроликам, равно числу пар репродуктивного возраста в предыдущем месяце, то есть количеству пар, которые уже родились два месяца назад. Теперь можно вычислить числа последовательности без необходимости изображения генеалогического древа кроликов.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

Для Фибоначчи эта последовательность носила в первую очередь характер бесконечной головоломки. Тем не менее способ определения популяции кроликов найдет в следующих столетиях много вариантов приложения: как практических, так и теоретических. Один из наиболее ярких примеров его применения можно найти в ботанике. Листорасположение – дисциплина, которая изучает, каким образом листья или различные элементы растения присоединяются к его основанию. Если вы внимательно посмотрите на шишку, вы увидите, что ее поверхность состоит из чешуек, которые закручиваются по спирали. Более конкретно можно подсчитать количество спиралей, которые закручиваются по часовой стрелке, и число спиралей, которые закручиваются в противоположном направлении.