Микаэль Лонэ - Большой роман о математике. История мира через призму математики

Короче говоря, эта бесконечная сумма на самом деле не позволит рассчитать точное значение числа π, а всего лишь позволяет обеспечить более точное приближение.

Поскольку мы не можем сложить все числа из бесконечного ряда, можно ограничиться определением суммы конечного числа чисел. Таким образом, если сложить первые пять чисел из ряда, мы получим 3,34.

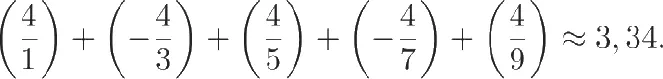
Это недостаточно точное приближение, но можно продолжать сложение чисел из ряда. Если мы возьмем первые сто чисел, получится 3,13, а если миллион, то 3,141592.

Разумеется, не очень удобно складывать миллион чисел, чтобы получить приближенное значение всего с шестью знаками после запятой. Ряд Мадхавы оказался неудачным способом для вычисления числа π, т. к. требовалось сложить слишком много его чисел. В дальнейшем другие математики, такие как швейцарец Леонард Эйлер в XVIII в., а также индийский ученый Сриниваса Рамануджан Айенгор в XX в. открыли ряд других рядов чисел, сумма которых равна π, но со значительно меньшим количеством чисел. Эти методы постепенно вытеснили метод Архимеда и позволили рассчитывать более точные значения с большим количеством знаков после запятой.

Тригонометрические соотношения также можно представить в виде суммы бесконечных рядов чисел. Так, например, можно рассчитать значение косинуса заданного угла.

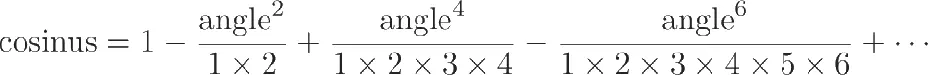
Для того чтобы рассчитать косинус, достаточно просто заменить слово «угол» в приведенной выше формуле на значение заданного угла. [14]Существуют похожие формулы для вычисления синуса, тангенса, а также ряда других чисел.

Вплоть до сего дня ряды чисел по-прежнему продолжают находить разнообразное применение. Ряд Фибоначчи до сих пор лежит в основе изучения динамики роста популяции и эволюции видов животных в течение длительного времени. Современные модели анализа, однако, учитывают гораздо больше факторов, таких как смертность, истребление хищниками, климат и изменение среды обитания животных. В целом ряды чисел используются в моделировании любого процесса, который прогрессивно продолжается на протяжении длительного времени. Сейчас они активно используются в информатике, статистике, экономике и даже метеорологии.

В начале XVI в. семена, посеянные Фибоначчи, начинают приносить свои плоды с появлением нового поколения математиков, возобновивших алгебраические исследования арабских ученых. Именно они в конечном счете смогли решить уравнения третьей степени совершенно невероятным способом.

Эта история началась в XVI в. с работ коммерсанта и профессора арифметики Болонского университета Сципиона дель Ферро. Он занимался исследованиями в области алгебры и был первым, кто смог описать решение уравнений третьей степени. Увы! В то время принцип повсеместного распространения знаний, который преобладал в арабском мире, еще не был распространен в Европе. Преподаватели Болонского университета плели интриги в борьбе за профессорский пост. Для того чтобы оставаться лучшим и не потерять свое место, дель Ферро стремился сохранить исследования в секрете от конкурентов. Он описал свое открытие, но не опубликовал его и посвятил в тайну исследований только нескольких учеников, которые, как и он, держали все в тайне.

Когда математик из Болоньи умер в 1526 г., итальянское математическое сообщество даже не догадывалось о том, что решение кубических уравнений уже найдено. Многие из ученых продолжали верить, что такие уравнения неразрешимы. Тем не менее один из учеников дель Ферро по имени Антонио Мария дель Фьоре, который был удостоен доверия своего учителя, не мог не воспользоваться его открытием. Он начал бросать вызов математикам из других стран, заключавшийся в основном в решении уравнений третьей степени. Разумеется, он выигрывал каждый раз. В результате слух о существовании решения постепенно начал распространяться по свету.

В 1535 г. дель Фьоре бросил вызов венецианскому ученому по имени Тарталья. Тому было 35 лет, и тогда еще не были опубликованы его важнейшие научные труды. Дель Фьоре не знал, что это был ученый, которому предстояло стать одним из лучших математиков своего поколения. Двое ученых направили друг другу список из тридцати вопросов, и поспорили на тридцать пиров, которые проигравший должен был закатить в честь победителя. В течение нескольких недель Тарталья раздумывал над решением уравнений третьей степени, посланных ему дель Фьоре, и за несколько дней до истечения срока ему удалось найти их решение! Он решил все тридцать задач и с легкостью выиграл пари.

История могла закончиться на этом, т. к. Тарталья отказался предать гласности свой метод. Так продолжалось еще четыре года.

Об этой дуэли узнал миланский математик и инженер по имени Джироламо Кардано. Переиначенное на французский манер его имя Жером Кардан, вероятно, знакомо автолюбителям: среди прочего он изобрел универсальный шарнир, используемый в автомобилях для передачи вращения двигателя на колеса. Кардано был среди тех, кто изначально считал невозможным решение уравнений третьей степени. Заинтригованный успехом Тартальи, он захотел встретиться с ним. В начале 1539 г. он отобрал восемь задач и попросил ученого объяснить его метод. Тарталья был категорически против. Кардано рассердился и пытался запугать упрямца, призвав алгебраистов страны осудить высокомерие их коллеги. Тарталья не поддавался.

В конечном счете Кардано пошел на уловку чтобы получить ответ на свой вопрос. Он сказал Тарталье, что маркиз Альваос, губернатор Милана, желает встретиться с ним. Живя в Венеции, Тарталья находился тогда в сложном положении и нуждался в покровителе. Он согласился поехать в Милан, где на 15 марта 1539 г. была назначена встреча в доме Кардано. Тарталья напрасно ждал губернатора в течение трех дней. Этого времени хватило, чтобы Кардано преодолел недоверие математика. После неустанных переговоров Тарталья в конце концов согласился поделиться своим открытием при условии, что Кардано поклянется никогда не публиковать его. Кардано дал слово и получил ответ на свой вопрос.

Вернувшись в Милан, Кардано начал анализировать полученные формулы. Метод работал, но не хватало самого главного: доказательства. До сих пор никому из математиков не удалось представить доказательство того, что их формулы верны. Именно этой задаче Кардано посвятил последующие годы своей жизни. Он смог это сделать, а один из его учеников, Лодовико Феррари, даже смог обобщить метод решения уравнений четвертой степени! Но данная в Милане клятва не позволяла математикам опубликовать результаты.