РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров краткое содержание
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Средняя геометрическая сделка также изменится. Вспомните уравнение (1.14) для средней геометрической сделки:
(1.14) GAT = G * (Наибольший проигрыш /-f),
где G = (среднее геометрическое) -1;
f=оптимальная фиксированная доля. (Разумеется, наш наибольший проигрыш всегда является отрицательным числом.)
Это уравнение эквивалентно следующему:
GAT = (среднее геометрическое - 1) * f$
Мы получили новое среднее геометрическое на основе приведенных данных. Переменная f$, которая была постоянной, когда прошлые данные не приводились, теперь изменится, так как она является функцией текущей цены. Таким образом, наша средняя геометрическая сделка меняется, когда меняется цена базового инструмента.
Порог геометрической торговли также должен измениться. Вспомните уравнение (2.02) для порога геометрической торговли:
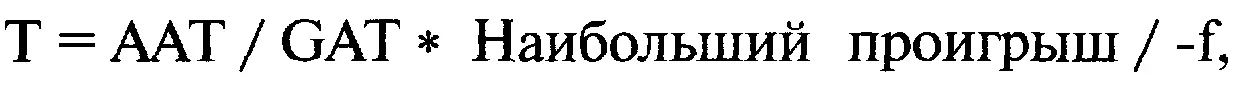
где Т = порог геометрической торговли;
ААТ = средняя арифметическая сделка;
GAT =средняя геометрическая сделка;
f= оптимальное f (от 0 до 1). Это уравнение также можно переписать следующим образом:
Т = ААТ/GAT* f$
Наконец, при сведении в единый портфель нескольких рыночных систем мы должны рассчитать ежедневные HPR. Это также функция f$:
(2.12) Дневное HPR = D$ / f$ + 1,
где D$ = долларовое изменение цены 1 единицы по сравнению с прошлым днем, т. е. (закрытие сегодня - закрытие вчера) * (доллары за пункт);
f$= текущее оптимальное f в долларах, рассчитанное из уравнения (2.11). Здесь текущей ценой является закрытие последнего дня.
Предположим, некая акция сегодня вечером закрылась на уровне 99 долларов. На прошлой сессии ее цена была 102 доллара. Наибольший процентный проигрыш равен -15. Если f= 0,09, тогда f$ равно:
f$ =-0,15*102*1/-0,09 =-15,3/-0,09 = 170
Так как мы имеем дело только с одной акцией, цена одного пункта составляет 1 доллар. Мы можем теперь определить сегодняшнее дневное HPR из уравнения (2.12):
(2.12) Дневное HPR = (99 -102) * 1 / 170 + 1 =-3/170+1
= -0,01764705882 + 1 = 0,9823529412
Теперь вернемся к началу нашей дискуссии. При потоке торговых P&L оптимальное f позволит получить наибольший геометрический рост (при условии, что арифметическое математическое ожидание положительное)'. Мы используем поток торговых P&L в качестве образца распределения возможных результатов в следующей сделке. Если привести к текущей цене поток прошлых прибылей и убытков, то мы сможем получить более правдоподобное распределение потенциальных прибылей и убытков для следующей сделки. Таким образом, нам следует рассчитывать оптимальное f из этого измененного распределения прибылей и убытков. Это не означает, что, используя оптимальное f, рассчитанное на основе приведенных данных, мы выиграем больше. Как видно из следующего примера, все выглядит несколько иначе:
| P&L | Процент Цена f$ базового инструмента | Количество акций | Полный капитал | ||
| При f= 0,09 (торговля приведенным методом): | $10000 | ||||
| +2 | 0,1 | 20 | $33,33 | 300 | $10600 |
| -3 | -0,15 | 20 | $33,33 | 318 | $9646 |
| +10 | 0,2 | 50 | $83,33 | 115,752 | $10803,52 |
| -5 | -0,1 | 50 | $83,33 | 129,642 | $10155,31 |
| P&L | Процент Цена f$ базового инструмента | Количество акций | Полный капитал | ||
| При f= 0,17 (торговля неприведенным методом): | $10000 | ||||
| +2 | 0,1 | 20 | $29,41 | 340,02 | $10680,04 |
| -3 | -0,15 | 20 | $29,41 | 363,14 | $9 590,61 |
| +10 | 0,2 | 50 | $29,41 | 326,1 | $12851,61 |
| -5 | -0,1 | 50 | $29,41 | 436,98 | $10666,71 |
Однако если бы все сделки были рассчитаны на основе текущей цены (скажем, 100 долларов за акцию), приведенное оптимальное f позволило бы выиграть больше, чем необработанное оптимальное f.
Что лучше использовать? Следует ли нам определять оптимальное f (и его побочные продукты) на основе приведенных данных или лучше действовать обычным способом? Это больше вопрос ваших предпочтений. Все зависит от того, что более важно в инструменте, которым вы торгуете: процентные изменения или абсолютные изменения. Будет ли движение в 2 доллара по акции в 20 долларов то же, что и движение в 10 долларов по акции в 100 долларов? Посмотрим, например, на торги по доллару и немецкой марке. Будет ли движение в 0,30 пункта при 0,4500 то же, что и движение в 0,40 пункта при 0,6000? На мой взгляд, лучше использовать приведенные данные. С этим, однако, можно поспорить. Например, если акция с 20 долларов выросла до 100 долларов, и мы хотим определить оптимальное f, нам, возможно, потребуется использовать только текущие данные. Сделки, которые происходили при цене в 20 долларов за акцию, относятся к рынку, значительно отличающемуся от существующего в настоящий момент.
Лучше не использовать данные, когда базовый инструмент был на совершенно другом ценовом уровне, так как состояние рынка могло существенно измениться В этом смысле оптимальное f на основе необработанных данных и оптимальное f, получаемое из приведенных данных, будут почти идентичны, когда все сделки происходят при ценах, близких к текущей цене базового инструмента.
Если действительно большое значение имеет то обстоятельство, приводите вы данные или нет, значит вы используете слишком много исторических данных. На самом деле, нет большой разницы, используете ли вы приведенные или необработанные данные, если нет вышеописанной проблемы, поэтому следует пользоваться приведенными данными. Это не означает, что оптимальное f, рассчитанное из приведенных данных, было оптимальным в прошлом. Оно могло таковым и не быть. Оптимальное f, рассчитанное из необработанных данных, могло быть оптимальным в прошлом. Однако оптимальное f, рассчитанное из приведенных данных, имеет больше смысла, так как приведенные данные являются более справедливым представлением распределения возможных результатов по следующей сделке.
Уравнения с (2. 10а) по (2. 10в) дают разные ответы в зависимости от того, какая была открыта позиция: длинная или короткая. Например, если акция куплена за 80, а продана за 100, выигрыш составит 25%. Однако если акция продана по 100, а закрыта по 80, то выигрыш составит только 20%. В обоих случаях позицию открыли по 80 и закрыли по 100. Таким образом, последовательность — хронология трансакций — должна приниматься во внимание. Так как хронология трансакций затрагивает распределение процентных выигрышей и проигрышей, мы допускаем, что будущая хронология скорее всего будет подобна прошлой. Конечно, мы можем игнорировать хронологию сделок (используя 2.10в для длинных позиций и цену выхода в знаменателе 2.10в для коротких позиций), но это означало бы уменьшение информации в исторических данных. Более того,
Читать дальшеИнтервал:
Закладка:










