РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров

Данный принцип справедлив независимо от того, насколько длинный или короткий период времени вы рассматриваете. Мы можем находиться в проигры­ше приблизительно от 35 до 55% времени за весь период работы торговой про­граммы! Это верно независимо от того, используем мы одну рыночную систему или портфель. Поэтому надо быть готовыми к периодам проигрыша 35-55% вре­мени торговой программы, тогда мы сможем психологически подготовиться к торговле в эти периоды.

Собираетесь ли вы управлять чьим-то счетом, отдать деньги в управление или торговать со своего собственного счета, вы должны помнить о законах арксинуса и знать, что может произойти с кривой баланса, а также помнить правило 35-55%. Таким образом, вы будете готовы к тому, что может произойти в будущем. Мы достаточно подробно изучили эмпирические подходы. Кроме того, мы обсуди­ли многие характеристики торговли фиксированной долей и узнали некоторые полез­ные методы, которые будут использоваться в дальнейшем. Мы увидели, что при тор­говле на оптимальных уровнях следует ожидать не только значительных падений баланса счета, но и длительного периода времени, необходимого для того, чтобы сно­ва заработать проигранные деньги. В следующей главе мы поговорим о параметри­ческих подходах.

Глава 3

Параметрическое оптимальное f при нормальном распределении

Теперь, когда мы закончили рассмотрение эмпирических методов, а также характеристик торговли фиксированной долей, мы изу­чим параметрические методы. Эти методы отличаются от эм­пирических тем, что в них не используется прошлая история в качестве данных, с которыми придется работать. Мы просто наблюдаем за прошлой историей для создания математического описания распределения исторических данных. Это математи­ческое описание основывается на том, что произошло в прошлом, а также на том, что, как мы ожидаем, произойдет в будущем. В параметрических методах мы имеем дело с этими математичес­кими описаниями, а не с самой прошлой историей. Математические описания, используемые в параметрических ме­тодах, называются распределениями вероятности. Чтобы ис­пользовать параметрические методы, мы должны сначала изу­чить распределения вероятности. Затем мы перейдем к изучению очень важного типа распределения, нормального распределения. Мы узнаем, как найти оптимальное/и его побочные продукты при нормальном распределении.

Основы распределений вероятности

Представьте себе, что вы находитесь на ипподроме и ведете запись мест, на которых лошади финишируют в забегах. Вы записываете, какая лошадь пришла первой, ка­кая второй и так далее для каждого забега. Учитываются только первые десять мест. Если лошадь пришла после десятой, то вы запишете ее на десятое место. Через не­сколько дней вы соберете достаточное количество информации и увидите распреде­ление финишных мест для каждой лошади. Теперь вы можете взять полученные данные и нанести на график. По горизонтальной оси будут отмечаться места, на ко­торых лошадь финишировала, слева на оси будет наихудшее место (десятое), а спра­ва наилучшее (первое). На вертикальной оси мы будем отмечать, сколько раз бего­вая лошадь финишировала в позиции, отмеченной на горизонтальной оси. Вы уви­дите, что построенная кривая будет иметь колоколообразную форму.

При таком сценарии есть десять возможных финишных мест для каждого за­бега. Мы будем говорить, что в этом распределении — десять ячеек (bins). Посмот­рим, что произойдет, если вместо десяти мы будем использовать пять ячеек. Пер­вая ячейка будет для первого и второго места, вторая ячейка для третьего и четвер­того места и так далее. Как это отразится на результатах?

Использование меньшего количества ячеек при том же наборе данных в резуль­тате дало бы распределение вероятности с тем же профилем, что и при большом количестве ячеек. То есть графически они бы выглядели примерно одинаково. Од­нако использование меньшего количества ячеек уменьшает информационное со­держание распределения, и наоборот, использование большего количества ячеек повышает информационное содержание распределения. Если вместо финишных позиций лошадей в каждом забеге мы будем записывать время, за которое пробежа­ла лошадь, округленное до ближайшей секунды, то получим не десять ячеек, а боль­ше, и, таким образом, информационное содержание распределения увеличится.

Если бы мы записали точное время финиша, а не округленное до секунд, то могли бы построить непрерывное распределение. При непрерывном распределе­нии нет ячеек. Представьте непрерывное распределение как серию бесконечно малых ячеек (см. рисунок 3-1). Непрерывное распределение отличается от диск­ретного, которое является ячеистым распределением. Хотя создание ячеек умень­шает информационное содержание распределения, в реальной жизни это един­ственно возможный подход для обработки ячеистых данных, поэтому на практи­ке приходится жертвовать частью информации, сохраняя при этом профиль распределения. И наконец, вы должны понимать, что можно взять непрерывное распределение и сделать его дискретным путем создания ячеек, но невозможно дискретное распределение переделать в непрерывное.

Когда мы имеем дело с торговыми прибылями и убытками, то чаще всего рас­сматриваем непрерывное распределение. Сделка может иметь множество исходов (хотя мы можем округлить цены до ближайшего цента). Для того чтобы работать с

таким распределением, потребуется разбить данные на ячейки, например шириной 100 долларов. Такое распределение имело бы отдельную ячейку для сделок, прибы­ли которых оказались ниже 99,99 доллара, другую ячейку для сделок от 100 до 199,99 доллара и так далее. При таком подходе будет определенная потеря информации, но профиль распределения торговых прибылей и убытков не изменится.

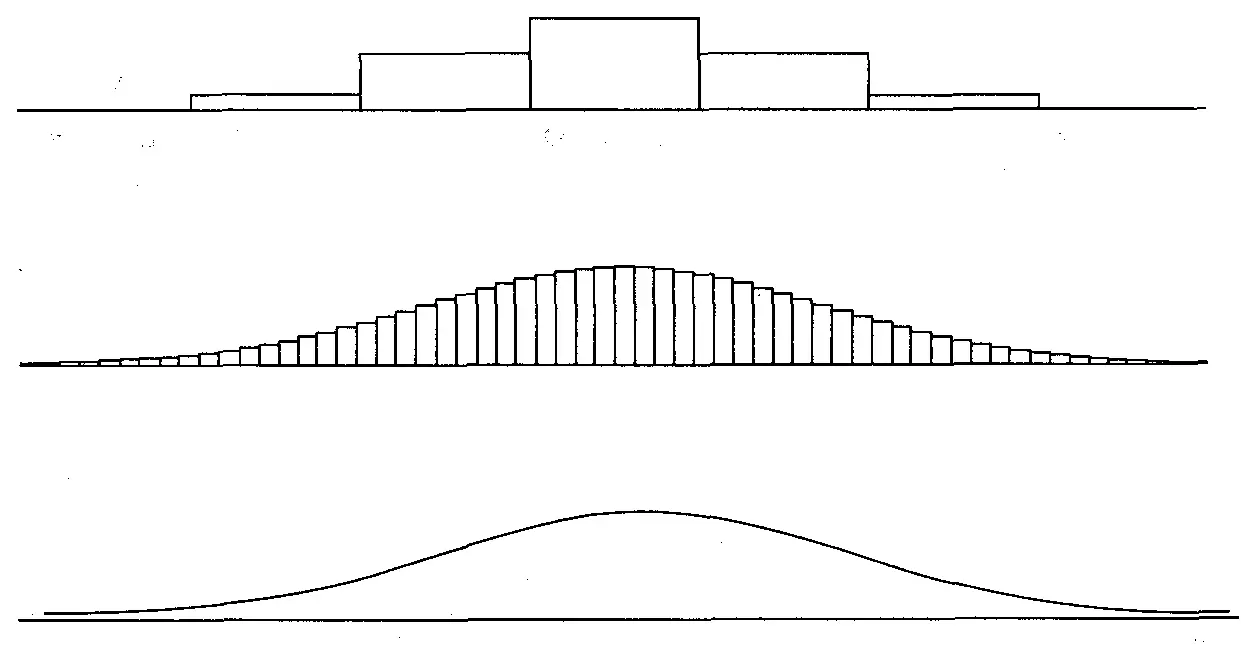
Рисунок 3-1 Непрерывное распределение является серией бесконечно малых ячеек.

Величины, описывающие распределения

Многие из вас наверняка знакомы со средним, или, если говорить точнее, средним арифметическим (arithmetic mean). Это просто сумма значений, соответствующих точкам распределения, деленная на количество точек данных:

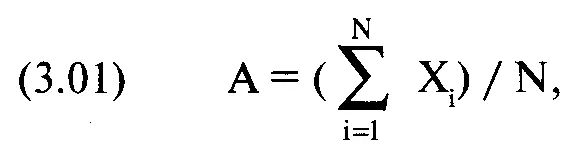
где А = среднее арифметическое;

X. = значение, соответствующее точке i;

N = общее число точек данных в распределении.

Среднее арифметическое является самым распространенным из набора величин, оценивающих расположение (location) или центральную тенденцию (central tendency) тела данных распределения. Однако вы должны знать, что среднее арифметическое является не единственным доступным измерением центральной тенденции, и зача­стую не самым лучшим. Среднее арифметическое обычно оказывается плохим вы­бором, когда распределение имеет широкие хвосты (tails [11] Область больших отклонении. — Прим. ред ). Если при исследовании распределения с очень широкими хвостами вы случайным образом будете выби­рать точки данных для расчета среднего, то, проделав это несколько раз подряд, увидите, что средние арифметические, полученные таким способом, заметно отли­чаются друг от друга. Еще одной важной величиной, определяющей расположение распределения, явля­ется медиана (median). Медиана описывает среднее значение, когда данные расположе­ны по порядку в соответствии с их величиной. Медиана делит распределение вероятно­сти на две половины таким образом, что площадь под кривой одной половины равна площади под кривой другой половины. В некоторых случаях медиана лучше задает центральную тенденцию, чем среднее арифметическое. В отличие от среднего арифме­тического медиана не искажается крайними случайными значениями. Более того, ме­диану можно рассчитать даже для распределения, в котором все значения выше задан­ной ячейки попадают в определенную ячейку. Примером такого распределения явля­ется рассмотренный выше забег лошадей. Любое финишное место после десятого записывается в десятое место. Медиана широко используется в Бюро Переписи США. Третьей величиной, определяющей центральную тенденцию, является мода (mode) — наиболее часто повторяющееся событие (или значение данных). Мода — это пик кривой распределения. В некоторых распределениях нет моды, а иногда есть более чем одна мода. Как и медиана, мода в некоторых случаях может лучше всего описывать центральную тенденцию. Мода никак не зависит от крайних случайных значений, и ее можно рассчитать быстрее, чем среднее арифметическое или медиану. Мы увидели, что медиана делит распределение на две равные части. Таким же образом распределение можно разделить тремя квартилями (quartiles), чтобы по­лучить четыре области равного размера или вероятности, или девятью децилями (deciles), чтобы получить десять областей равного размера или вероятности, или 99 перцентилями (percentiles) (чтобы получить 100 областей равного размера или вероятности), 50-й перцентиль является медианой и вместе с 25-м и 75-м перцен­тилями дает нам квартили. И наконец, еще один термин, с которым вы должны познакомиться, — это квантиль (quantile). Квантиль — это некоторое число N-1, которое делит общее поле данных на N равных частей. Теперь вернемся к среднему. Мы обсудили среднее арифметическое, которое изме­ряет центральную тенденцию распределения. Есть и другие виды средних, они реже встречаются, но в определенных случаях также могут оказаться предпочтительнее. Одно из них — это среднее геометрическое (geometric mean), расчет которого дан в первой главе. Среднее геометрическое является корнем степени N из произведе­ния значений, соответствующих точкам распределения.