РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров

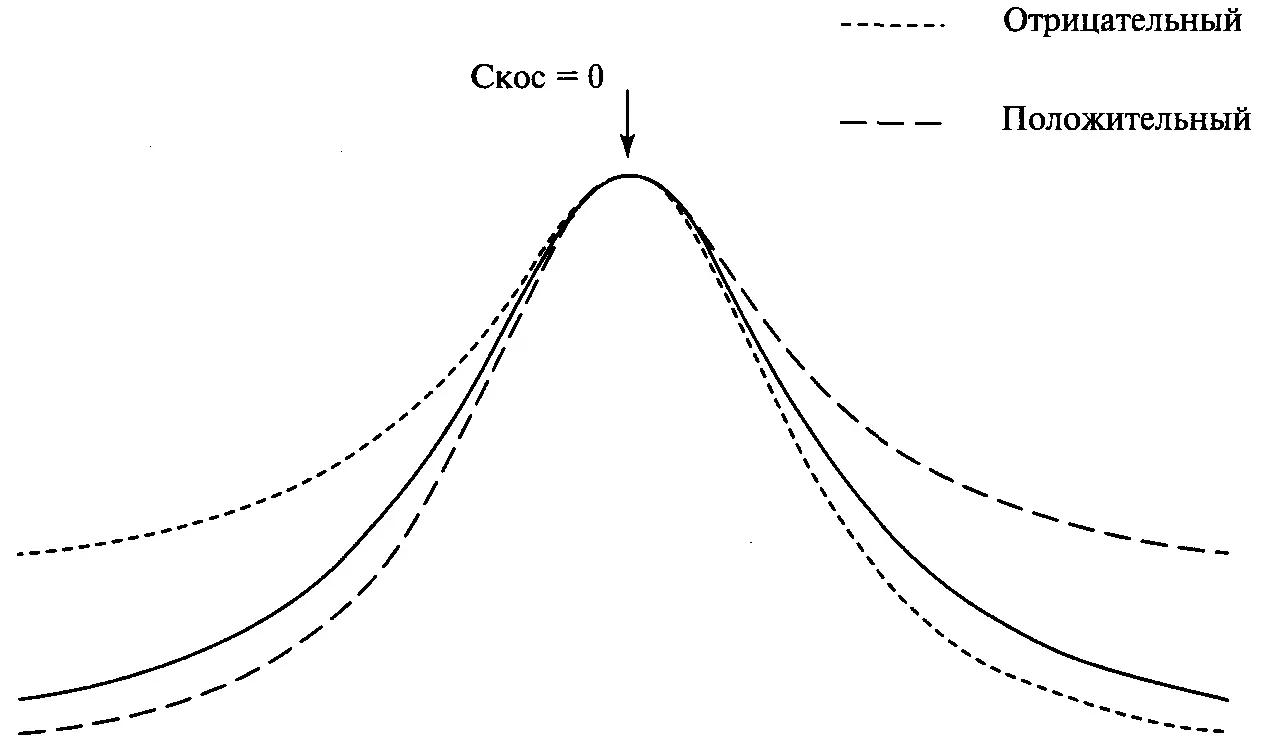
Рисунок3-2 Асимметрия

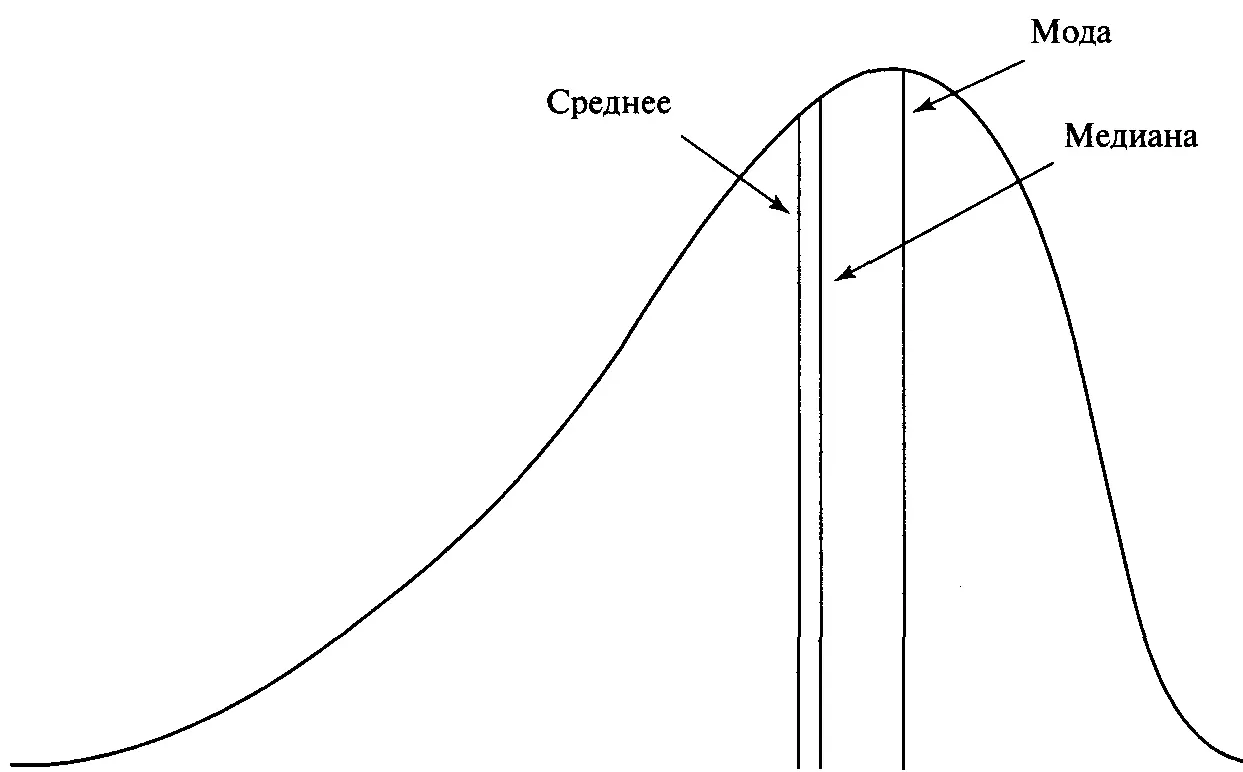
Рисунок3-3 Асимметричное распределение

В симметричном распределении среднее, медиана и мода имеют одинаковое значе­ние. Однако когда распределение имеет ненулевое значение асимметрии, оно может принять вид, показанный на рисунке 3-3. Для асимметричного распределения (лю­бого распределения с ненулевой асимметрией) верно равенство:

(3.08) Среднее - Мода = 3 * (Среднее - Медиана)

Есть много способов для расчета асимметрии, и они часто дают различные отве­ты. Ниже мы рассмотрим несколько вариантов:

(3.09) S == (Среднее - Мода) / Стандартное отклонение

(3.10) S = (3 * (Среднее - Медиана)) / Стандартное отклонение

Уравнения (3.09) и (3.10) дают нам первый и второй коэффициенты асимметрии Пирсона. Асимметрия также часто определяется следующим образом:

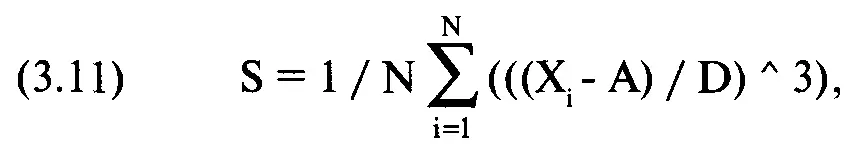
где S = асимметрия;

N = общее число точек данных;

Х = значение, соответствующее точке i;

А = среднее арифметическое значений точек данных;

D = стандартное отклонение значений точек данных.

И наконец, четвертый момент распределения, эксцесс (kurtosis) (см. рисунок 3-4), измеряет, насколько у распределения плоская или острая форма (по сравнению с нормальным распределением). Как и асимметрия, это безразмерная величина. Кривая, менее остроконечная, чем нормальная, имеет эксцесс отрицательный, а кривая, более остроконечная, чем нормальная, имеет эксцесс положительный. Когда пик кривой такой же, как и у кривой нормального распределения, эксцесс равен нулю, и мы будем говорить, что это распределение с нормальным эксцессом.

Как и предыдущие моменты, эксцесс имеет несколько способов расчета. Наи­более распространенными являются:

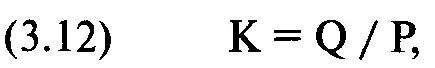
где К = эксцесс;

Q == семи-интерквартильная широта;

Р = широта перцентиля 10-90.

(3.13) К = (1 / N (∑ (((X - А i) / D)^ 4))) - 3,

где К = эксцесс;

N = общее число точек данных;

Х = значение, соответствующее точке i;

А = среднее арифметическое значений точек данных;

D = стандартное отклонение значений точек данных.

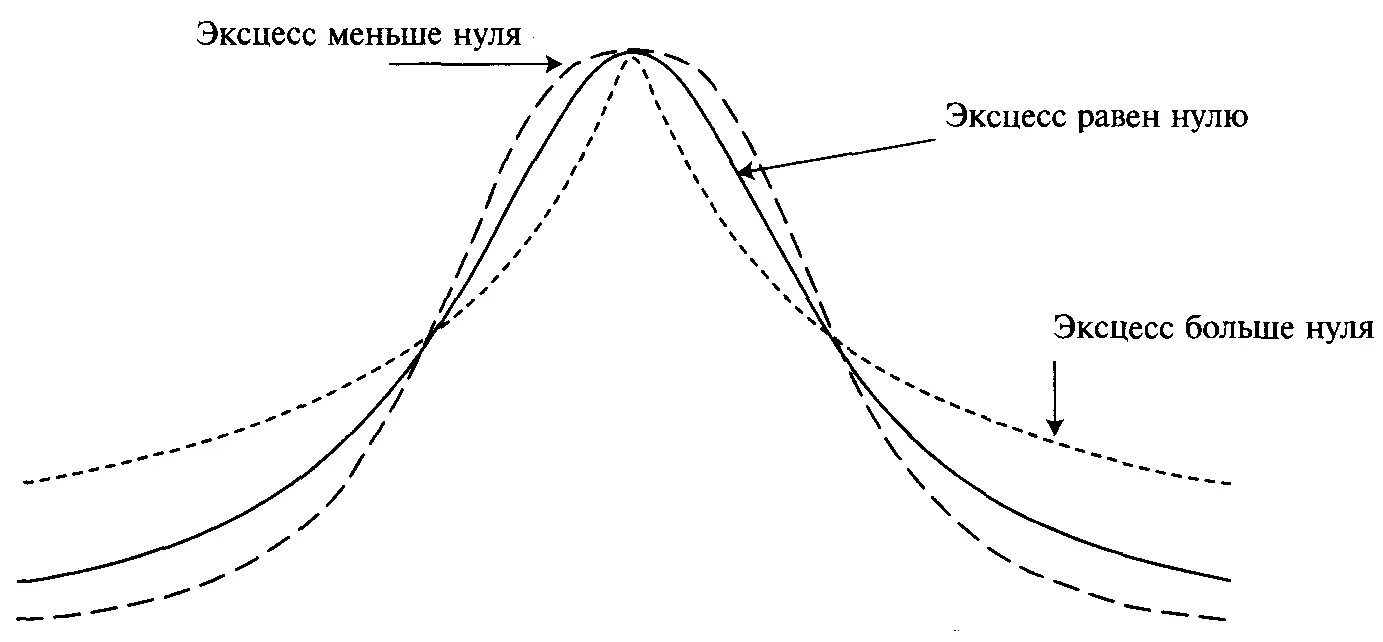
Рисунок3-4 Эксцесс

Наконец, необходимо отметить, что «теория», связанная с моментами распределе­ния, намного серьезнее, чем то, что представлено здесь. Для более глубокого пони­мания вам следует просмотреть книги по статистике, упомянутые в списке реко­мендованной литературы. Для наших задач изложенного выше вполне достаточно.

До настоящего момента рассматривалось распределение данных в общем виде. Теперь мы изучим нормальное распределение.

Нормальное распределение

Часто нормальное распределение называют распределением Гаусса, или Муавра, в честь тех, кто, как считается, открыл его — Карл Фридрих Гаусс (1777-1855) и, веком ранее, что не так достоверно, Авраам де Муавр (1667-1754). Нормальное распределение считается наиболее ценным распределением, благо­даря тому, что точно моделирует многие явления. Давайте рассмотрим приспособление, более известное как доска Галтона (ри­сунок 3-5). Это вертикально установленная доска в форме равнобедренного треу­гольника. В доске расположены колышки, один в верхнем ряду, два во втором, и так далее. Каждый последующий ряд имеет на один колышек больше. Колышки в сечении треугольные, так что, когда падает шарик, у него есть вероятность 50/50 пойти вправо или влево. В основании доски находится серия желобов для подсче­та попаданий каждого броска.

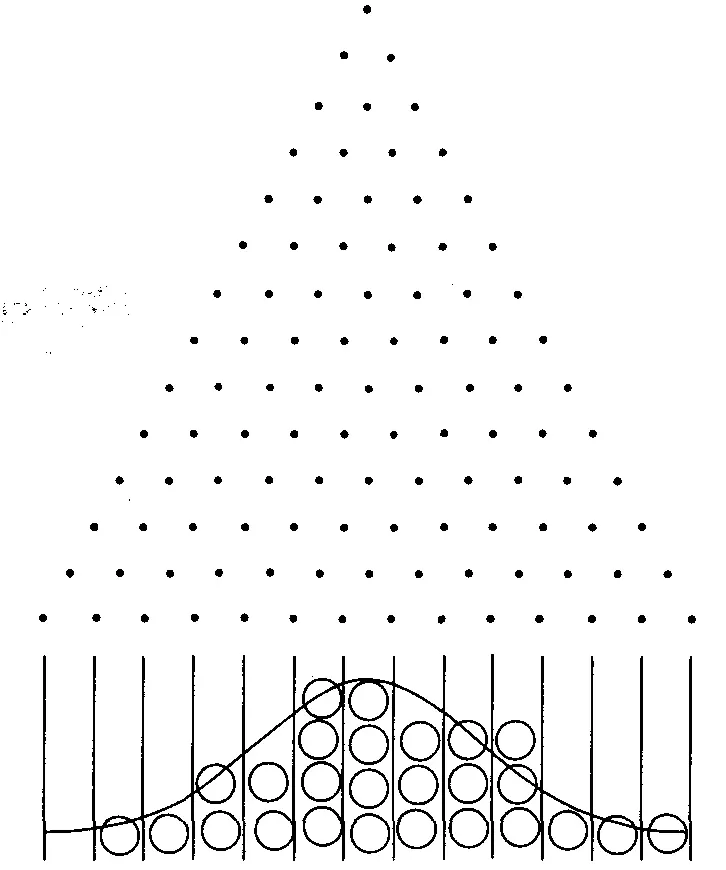
Рисунок3-5 Доска Галтона

Шарики, падающие через доску Галтона и достигающие желобов, начинают фор­мировать нормальное распределение. Чем «глубже» доска (то есть чем больше ря­дов она имеет) и чем больше шариков бросается, тем ближе конечный результат будет напоминать нормальное распределение.

Нормальное распределение интересно еще и потому, что оно является пре­дельной формой многих других типов распределений. Например, если Х распре­делено биномиально, а N стремится к бесконечности, то Х стремится к нор­мальному распределению. Более того, нормальное распределение также является предельной формой многих других ценных распределений вероятности, таких как Пуассона, Стьюдента (или t-распределения). Другими словами, когда коли­чество данных (N), используемое в этих распределениях, увеличивается, они все более напоминают нормальное распределение.

Центральная предельная теорема

Одно из наиболее важных применений нормального распределения относится к распределению средних значений. Средние значения выборок заданного разме­ра, взятые таким образом, что каждый элемент выборки отобран независимо от других, дадут распределение, которое близко к нормальному Это чрезвычайно важный факт, так как он означает, что вы можете получить параметры действи­тельно случайного процесса из средних значений, рассчитанных на основе выбо­рочных данных.

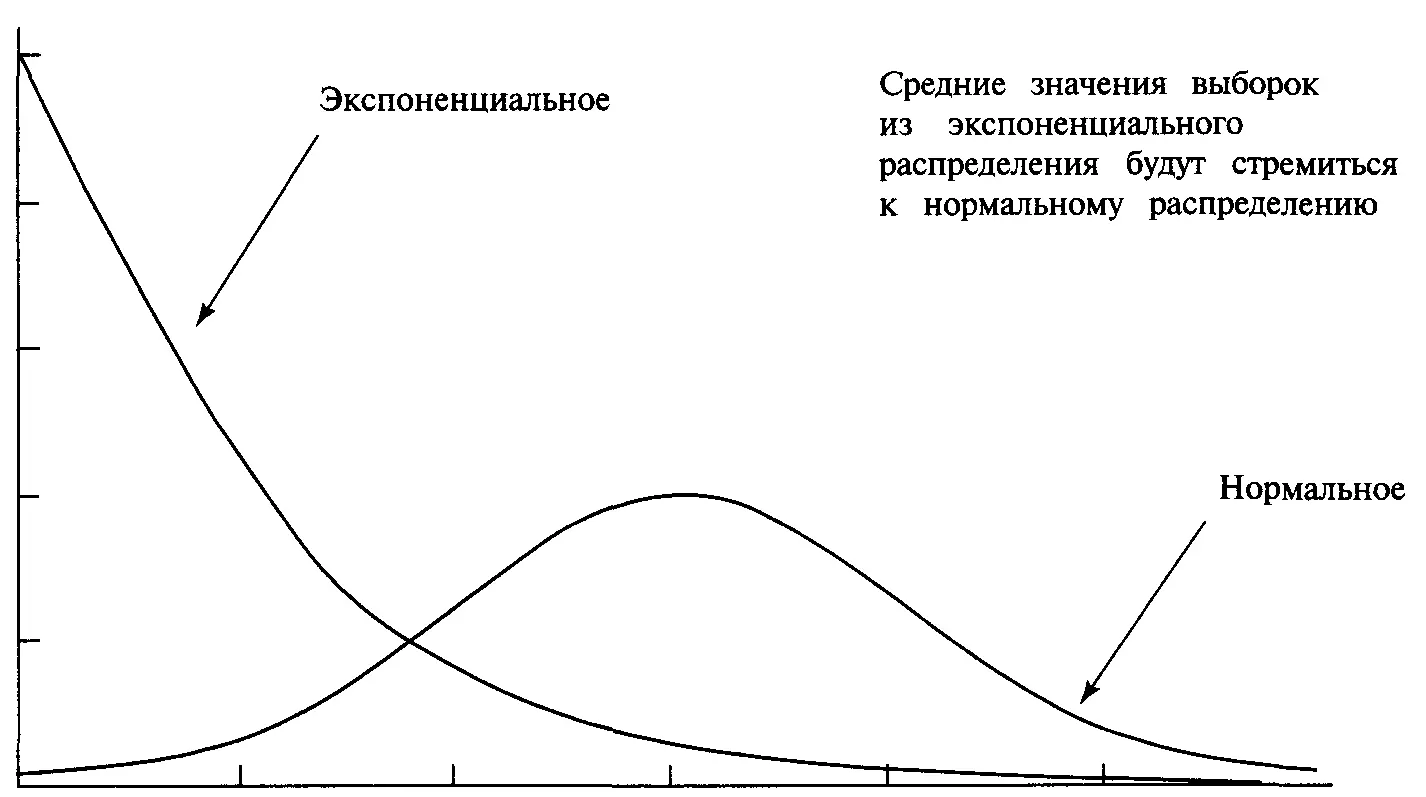
Рисунок3-6 Экспоненциальное распределение и нормальное распределение

Таким образом, мы можем сформулировать, что если N случайных выборок извлека­ются из совокупности всех данных, тогда суммы (или средние значения) выборок бу­дут приблизительно нормально распределяться независимо от распределения сово­купности, из которой взяты эти выборки. Близость к нормальному распределению увеличивается, когда N (число выборок) возрастает. В качестве примера рассмот­рим распределение чисел от 1 до 100. Это равномерное распределение, где все эле­менты (в данном случае числа) встречаются только раз. Например, число 82 встречается один раз, так же как и 19, и так далее. Возьмем выборку из пяти эле­ментов и среднее значение этих пяти элементов (мы можем также взять их сумму). Теперь поместим полученные пять элементов обратно, возьмем другую выборку и рассчитаем среднее. Если мы будем продолжать этот процесс дальше, то увидим, что полученные средние нормально распределяются, даже если совокупность, из которой они взяты, распределена равномерно.