РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров

2-хвостая вероятность (вне) = (1 - 0,9772499478) * 2 =0,02275005216*2 =0,04550010432

Наконец, мы рассмотрим случай, когда надо найти вероятности (площадь под кривой N'(Z)) для двух различных значений Z.

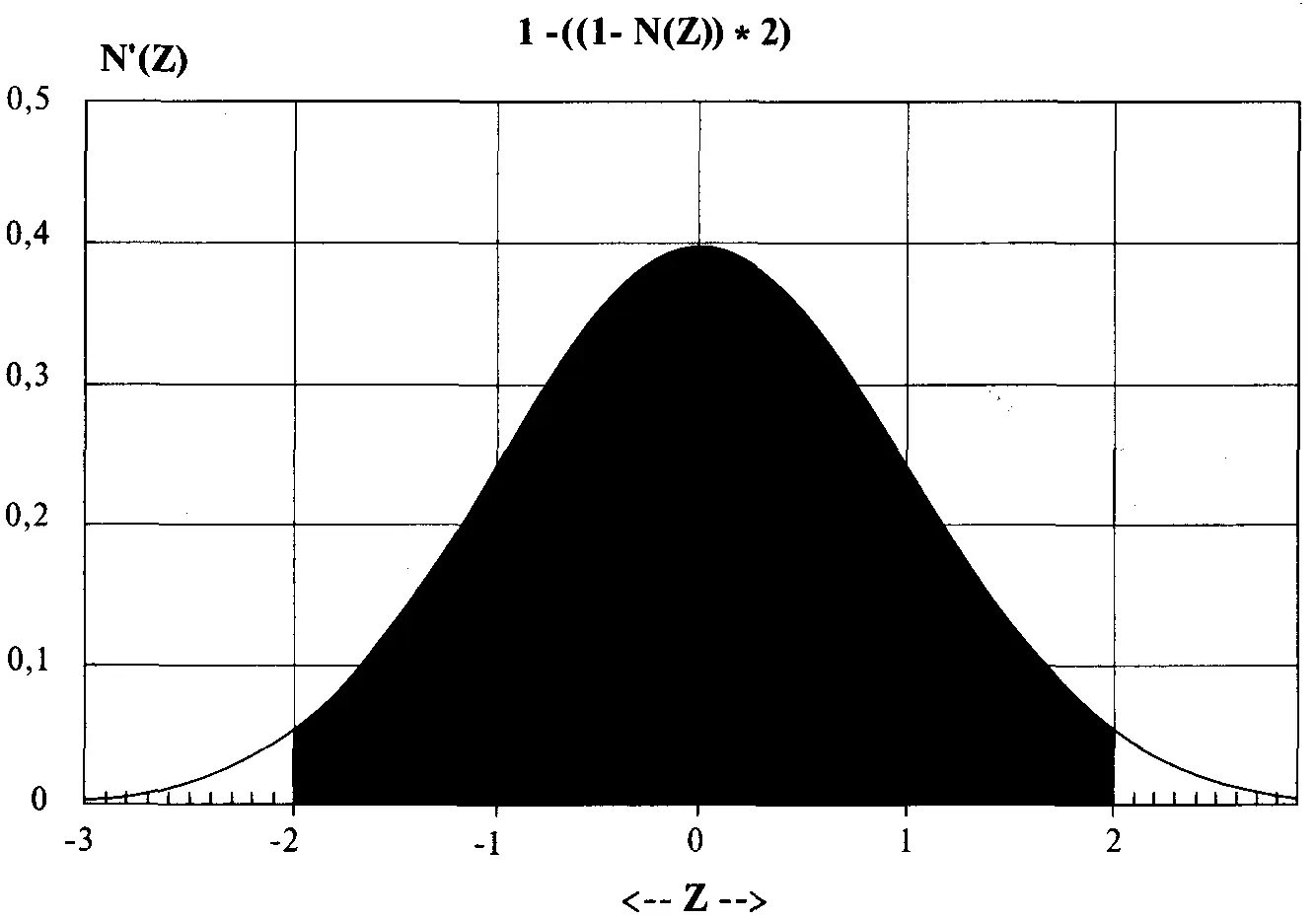
Рисунок 3-102-хвостая вероятность события между +2 и -2 сигма

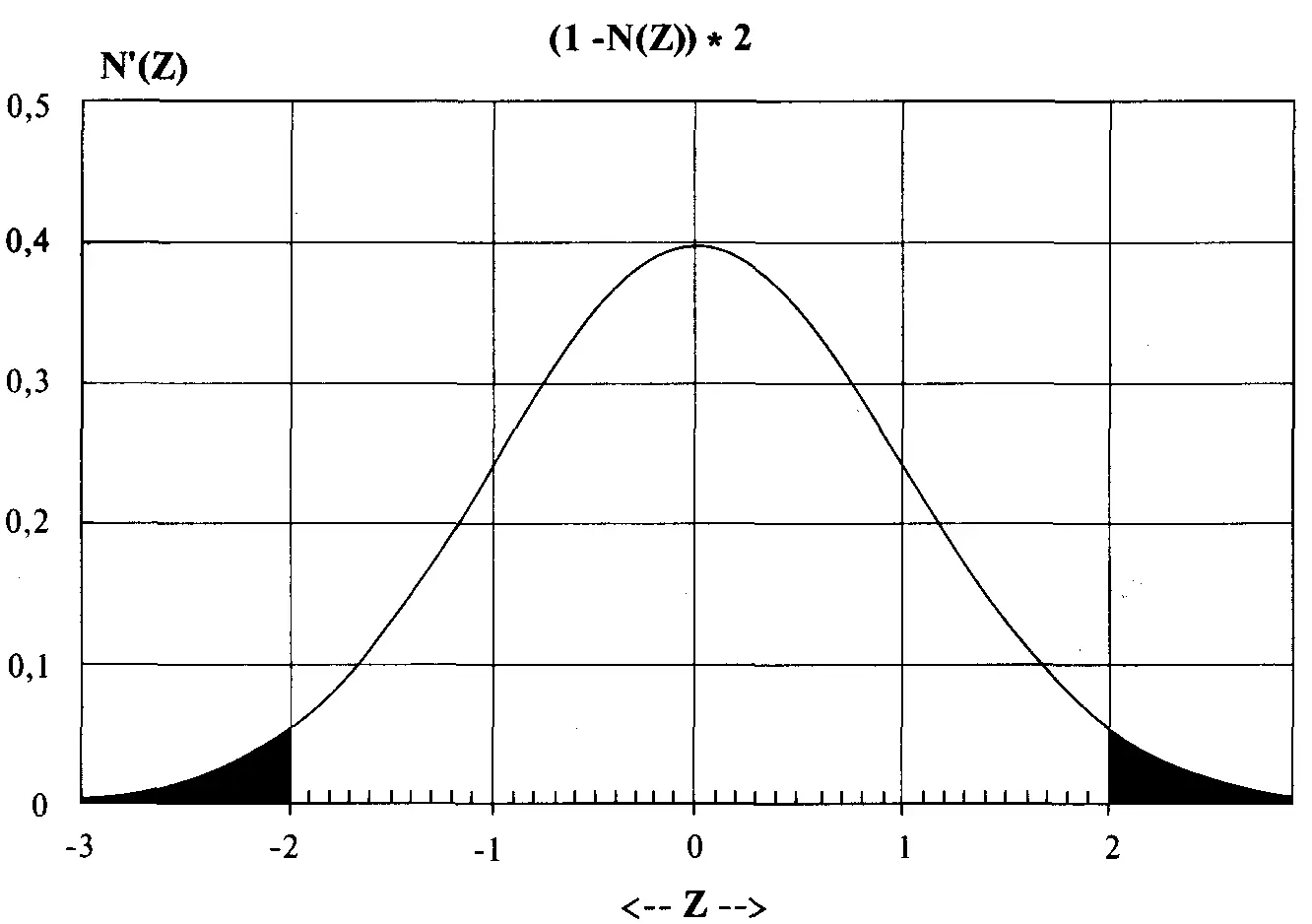
Рисунок 3-112-хвостая вероятность события, находящегося вне 2 сигма

Допустим, нам надо найти площадь под кривой N'(Z) между -1 стандартной еди­ницей и +2 стандартными единицами. Есть два способа расчета. Мы можем рассчитать вероятность, не превыша­ющую +2 стандартные единицы, при помощи уравнения (3.21) и вычесть ве­роятность, не превышающую -1 стандартную единицу (см. рисунок 3-12). Это даст нам:

0,9772499478 - 0,1586552595 = 0,8185946883

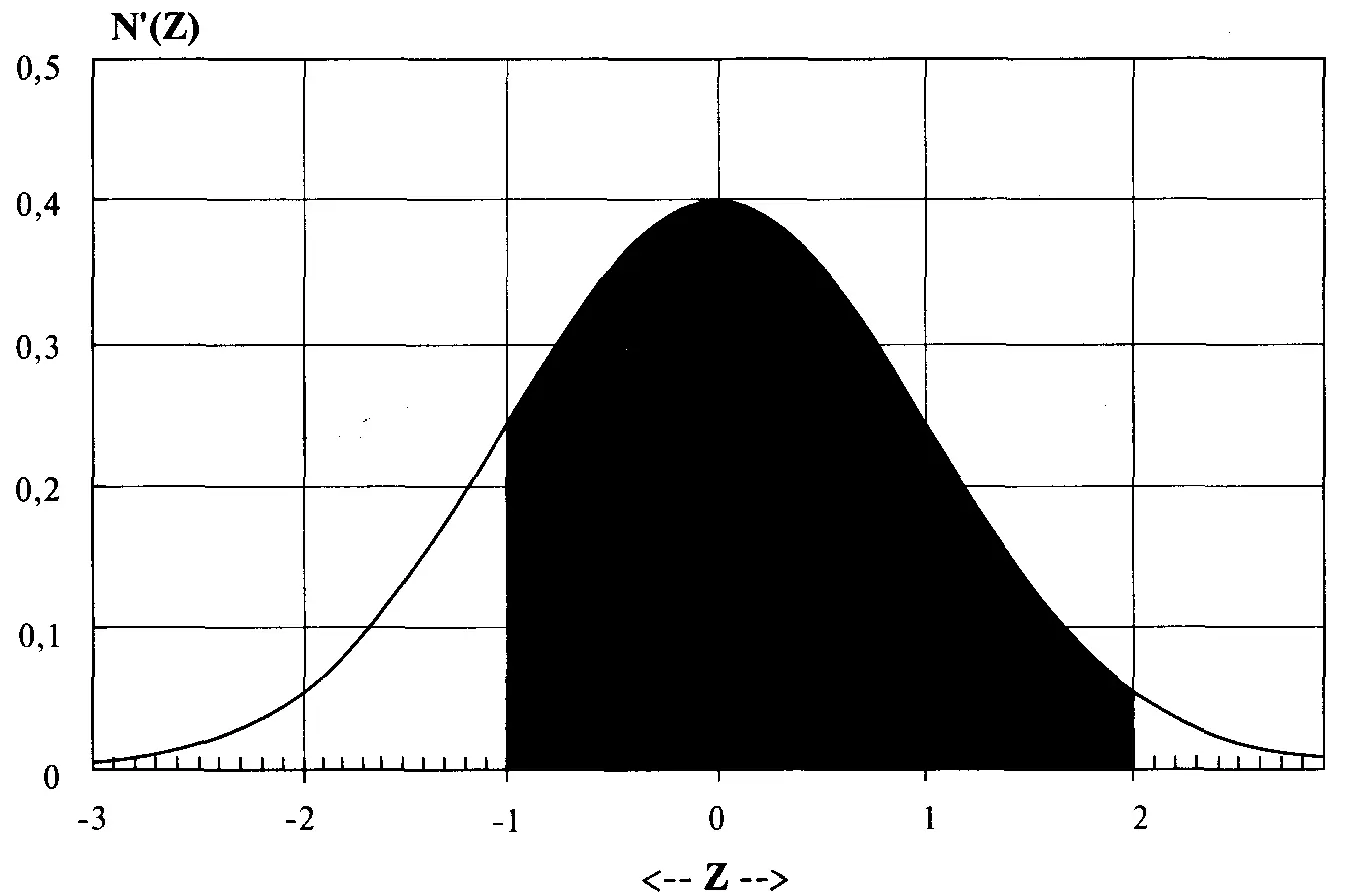
Рисунок 3-12Площадь между -1 и +2 стандартными единицами

Другой способ: из единицы, представляющей всю площадь под кривой, надо вы­честь вероятность, не превышающую -1 стандартную единицу, и вероятность, превышающую 2 стандартные единицы:

= 1 - (0,022750052 + 0,1586552595) = 1 -0,1814053117 =0,8185946883

С помощью рассмотренных в этой главе математических подходов вы сможете рассчитывать любые вероятности событий для случайных процессов, имею­щих нормальное распределение.

Последующие производные нормального распределения

Иногда требуется знать вторую производную функции N(Z). Так как функция N(Z) дает нам значение площади под кривой при Z, а функция N'(Z) дает нам высоту самой кривой при значении Z, тогда функция N"(Z) дает нам мгновенный наклон (instantaneous slope) кривой при данном значении Z:

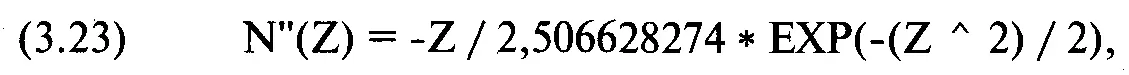
где ЕХР() = экспоненциальная функция.

Найдем наклон кривой N'(Z) при +2 стандартных отклонениях:

N"(Z) = -2 I 2,506628274 * ЕХР(-(+2^ 2) / 2) = -2 / 2,506628274 * ЕХР(-2) = -2 / 2,506628274 * 0,1353353 =-0,1079968336

Теперь мы знаем, что мгновенная скорость изменения функции N'(Z) при Z = +2 равна-0,1079968336. Это означает повышение/понижение за период, поэтому, когда Z = +2, кривая N'(Z) повышается на -0,1079968336. Эта ситуация показана на рисунке 3-13.

Последующие производные даются далее для справки. Они не будут использо­ваться в оставшейся части книги и представлены для полноты освещения темы:

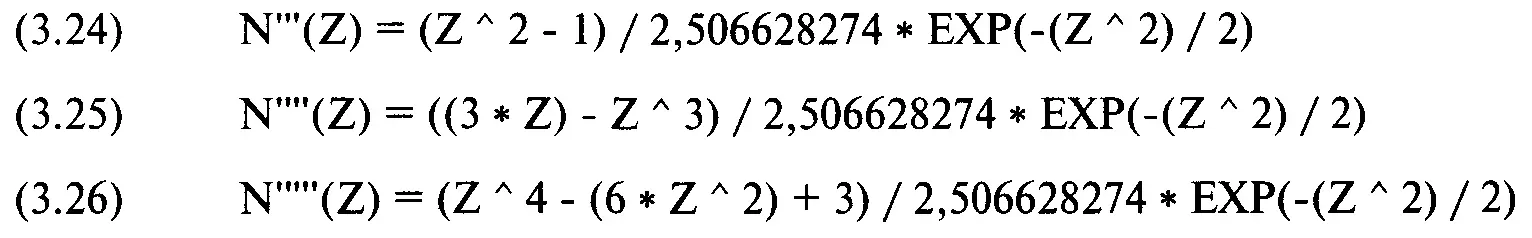
В качестве последнего дополнения к сказанному о нормальном распределении стоит заметить, что на самом деле это распределение не такое остроконечное, как на графиках, представленных в данной главе. Реальная форма нормального рас­пределения показана на рисунке 3-14. Отметьте, что здесь масштабы двух осей одинаковы, в то время как в других графических примерах они отличаются для придания более вытянутой формы.

Логарифмически нормальное распределение

Для торговли многие приложения требуют небольшой, но важной модификации нормального распределения.

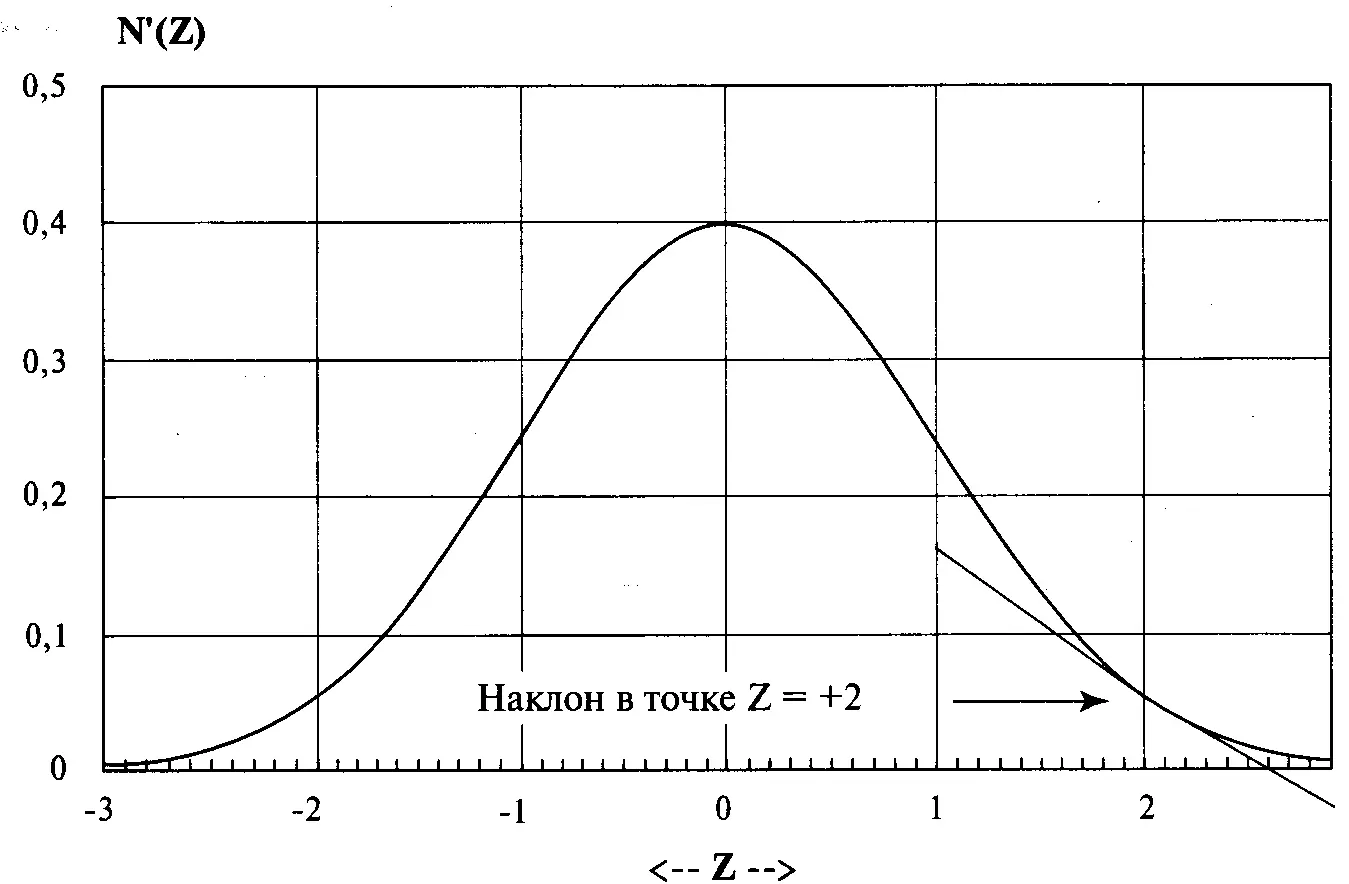
Рисунок 3-13N"(Z) дает наклон касательной к N'(Z) при Z = +2

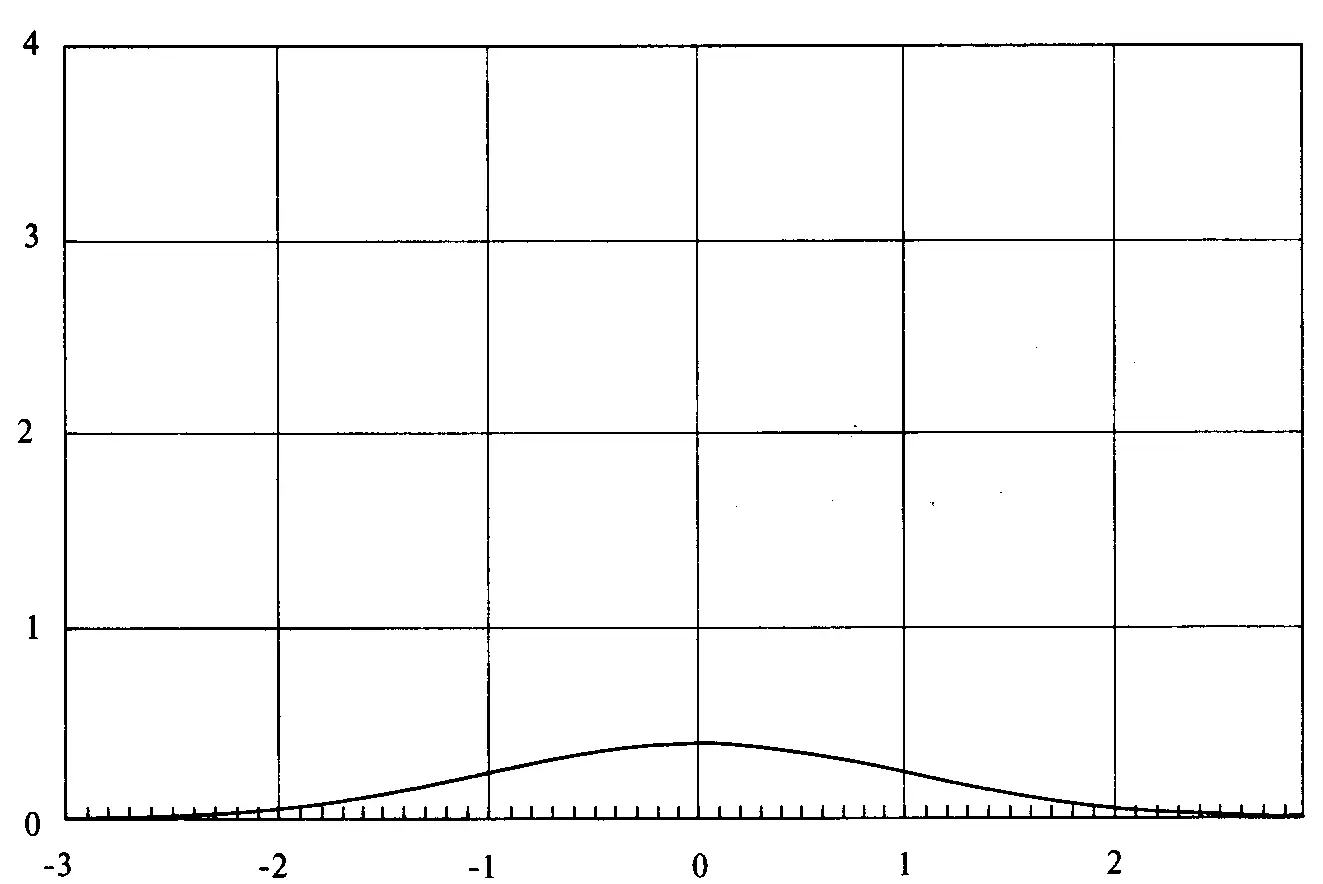
Рисунок 3-14Реальная форма нормального распределения

С помощью этой модификации нормальное распределение преобразуется в лога­рифмически нормальное распределение. Цена любого свободно котируемого инст­румента имеет нулевое значение в качестве нижнего предела [13] Предположение, что самой низкой ценой, по которой может торговаться инструмент, является ноль, не всегда верно. Например, во время краха фондового рынка в 1929 году и последующего медвежьего рьшка акционеры многих обанкротившихся банков понес­ли ответственность перед вкладчиками этих банков. Акционеры таких банков не только потеряли инвестированные в акции деньги, но также понесли убытки сверх этого . Поэтому когда цена этого инструмента падает и приближается к нулю, то, теоретически, цене инстру­мента должно быть все труднее понизиться. Рассмотрим некую акцию стоимостью 10 долларов. Если бы акция упала на 5 долларов до 5 долларов за акцию (50% пони­жение), то в соответствии с нормальным распределением она может также легко упасть с 5 долларов до 0 долларов. Однако при логарифмически нормальном рас­пределении подобное падение на 50% с цены в 5 долларов за акцию до цены 2,50 долларов за акцию будет примерно таким же вероятным, как и падение с 10 долла­ров до 5 долларов за акцию.

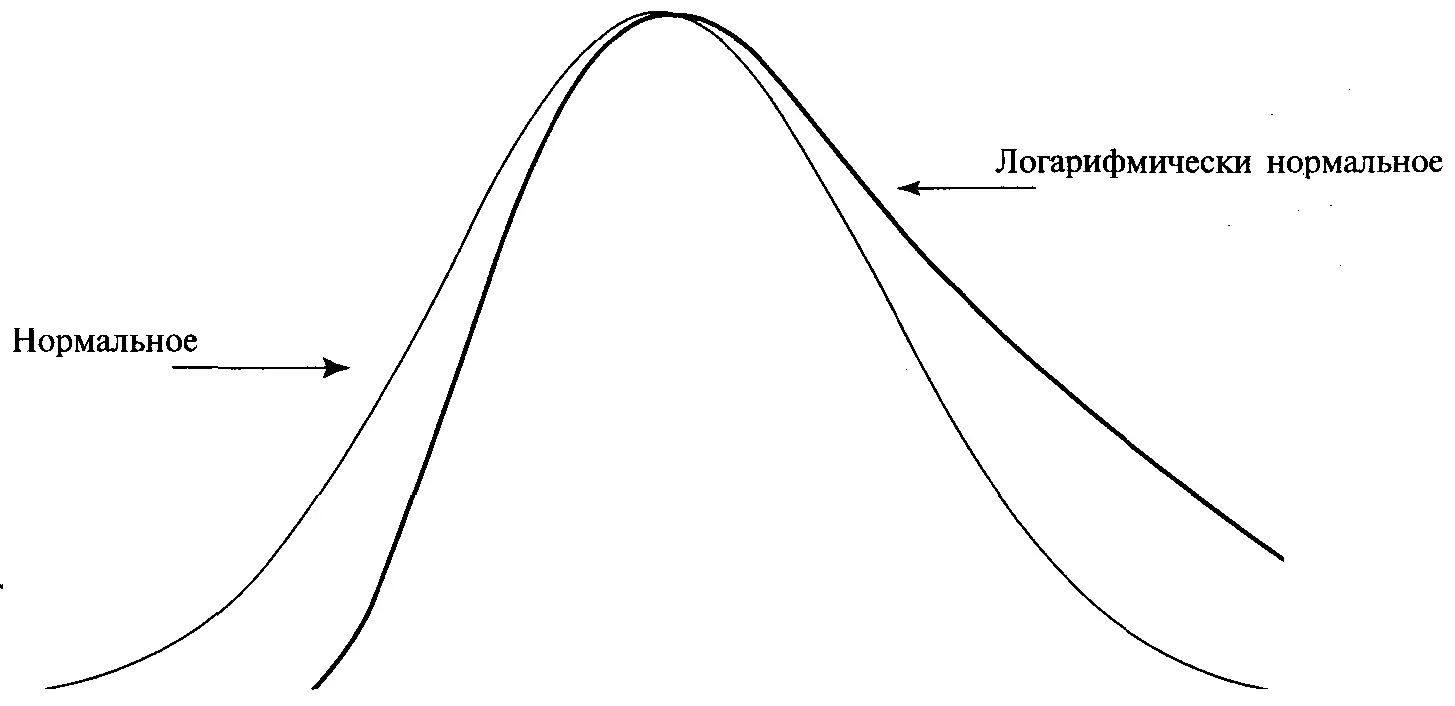
Рисунок 3-15Нормальное и логарифмически нормальное распределения

Логарифмически нормальное распределение, рисунок 3-15, работает точно так же, как и нормальное распределение, за тем исключением, что при логарифми­чески нормальном распределении мы имеем дело с процентными изменениями, а не абсолютными. Теперь рассмотрим движение вверх. В соответствии с логарифмически нормальным распределением движение с 10 долларов за акцию до 20 долларов за акцию анало­гично движению с 5 долларов до 10 долларов за акцию, так как оба эти движения представляют повышение на 100%. Это не означает, что мы не будем использовать нормальное распределение. Мы просто познакомимся с логарифмически нормаль­ным распределением, покажем его отличие от нормального (логарифмически нор­мальное распределение использует процентные, а не абсолютные изменения цены) и увидим, что обычно именно оно используется при обсуждении ценовых движений или в том случае, когда нормальное распределение ограничено снизу нулем. Для ис­пользования логарифмически нормального распределения необходимо преобразо­вывать данные, с которыми вы работаете, в натуральные логарифмы [14] Различие между десятичным и натуральным логарифмом следующее. Десятичный логарифм — это логарифм, который имеет в основании 10, в то время как натураль­ный логарифм имеет в основании число е, где е = 2,7182818285. Десятичный лога­рифм Х математически обозначается log(X), в то время как натуральный логарифм обозначается 1п(Х). Натуральный логарифм может быть преобразован в десятичный путем умножения натурального логарифма на 0,4342917. Таким же образом мы можем преобразовать десятичный логарифм в натуральный путем умножения десятич­ного логарифма на 2,3026. .