РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров краткое содержание
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Зачем вообще использовать эмпирические методы? Они интуитивно более очевидны, чем параметрические. Следовательно, эмпирические методы необходимо изучать до перехода к параметрическим. Мы уже достаточно подробно рассмотрели эмпирический подход и поэтому готовы изучать параметрические методы.
Распределение торговых прибылей и убытков (P&L)
Рассмотрим следующую последовательность 232 торговых прибылей и убытков в пунктах. Не имеет значения, к какому товару или системе относится этот поток данных — это может быть любая система на любом рынке.
| № сделки P&L | № сделки P&L | № сделки P&L | № сделки | P&L |
| 1. 0,18 | 25. 0,15 | 49. 0,17 | 73. | 0,22 |
| 2. -1,11 | 26. 0,15 | 50. -1,53 | 74. | 0,92 |
| 3. 0,42 | 27. -1,14 | 51. 0,15 | 75. | 0,32 |
| 4. -0,83 | 28. 1,12 | 52. -0,93 | 76. | 0,17 |
| 5. 1,42 | 29. -1,88 | 53. 0,42 | 77. | 0,57 |
| 6. 0,42 | 30. 0,17 | 54. 2,77 | 78. | 0,17 |
| 7. -0,99 | 31. 0,57 | 55. 8,52 | 79. | 1,18 |
| 8. 0,87 | 32. 0,47 | 56. 2,47 | 80. | 0,17 |
| 9. 0,92 | 33. -1,88 | 57. -2,08 | 81. | 0,72 |
| 10. -0,4 | 34. 0,17 | 58. -1,88 | 82. | -3,33 |
| 11. -1,48 | 35. -1,93 | 59. -1,88 | 83. | -4,13 |
| 12. 1,87 | 36. 0,92 | 60. 1,67 | 84. | -1,63 |
| 13. 1,37 | 37. 1,45 | 61. -1,88 | 85. | -1,23 |
| 14. -1,48 | 38. 0,17 | 62. 3,72 | 86. | 1,62 |
| 15. -0,21 | 39. 1,87 | 63. 2,87 | 87. | 0,27 |
| 16. 1,82 | 40. 0,52 | 64. 2,17 | 88. | 1,97 |
| 17. 0,15 | 41. 0,67 | 65. 1,37 | 89. | -1,72 |
| 18. 0,32 | 42. -1,58 | 66. 1,62 | 90. | 1,47 |
| 19. -1,18 | 43. -0,5 | 67. 0,17 | 91. | -1,88 |
| 20. -0,43 | 44. 0,17 | 68. 0,62 | 92. | 1,72 |
| 21. 0,42 | 45. 0,17 | 69. 0,92 | 93. | 1,02 |
| 22. 0,57 | 46. -0,65 | 70. 0,17 | 94. | 0,67 |
| 23. 4,72 | 47. 0,96 | 71. 1,52 | 95. | 0,67 |
| 24. 12,42 | 48. -0,88 | 72. -1,78 | 96. | -1,18 |
| Продолжение | ||||||
| № сделки | P&L | № сделки | P&L | № сделки | P&L | № сделки P&L |
| 97. | 3,22 | 126. | -1,83 | 155. | 0,37 | 184. 0,57 |
| 98. | -4,83 | 127. | 0,32 | 156. | 0,87 | 185. 0,35 |
| 99. | 8,42 | 128. | 1,62 | 157. | 1,32 | 186. 1,57 |
| 100. | -1,58 | 158. | 0,16 | 187. -1,73 | ||
| 101. | -1,88 | 130. | 1,02 | 159. | 0,18 | 188. -0,83 |
| 102. | 1,23 | 131. | -0,81 | 160. | 0,52 | 189. -1,18 |
| 103. | 1,72 | 132. | -0,74 | 161. | -2,33 | 190. -0,65 |
| 104. | 1,12 | 133. | 1,09 | 162. | 1,07 | 191. -0,78 |
| 105. | -0,97 | 134. | -1,13 | 163. | 1,32 | 192. -1,28 |
| 106. | -1,88 | 135. | 0,52 | 164. | 1,42 | 193. 0,32 |
| 107. | -1,88 | 136. | 0,18 | 165. | 2,72 | 194. 1,24 |
| 108. | 1,27 | 137. | 0,18 | 166. | 1,37 | 195. 2,05 |
| 109. | 0,16 | 138. | 1,47 | 167. | -1,93 | 196. 0,75 |
| 110. | 1,22 | 139. | -1,07 | 168. | 2,12 | 197. 0,17 |
| 111. | -0,99 | 140. | -0,98 | 169. | 0,62 | 198. 0,67 |
| 112. | 1,37 | 141. | 1,07 | 170. | 0,57 | 199. -0,56 |
| 113. | 0,18 | 142. | -0,88 | 171. | 0,42 | 200. -0,98 |
| 114. | 0,18 | 143. | -0,51 | 172. | 1,58 | 201. 0,17 |
| 115. | 2,07 | 144. | 0,57 | 173. | 0,17 | 202. -0,96 |
| 116. | 1,47 | 145. | 2,07 | 174. | 0,62 | 203. 0,35 |
| 117. | 4,87 | 146. | 0,55 | 175. | 0,77 | 204. 0,52 |
| 118. | -1,08 | 147. | 0,42 | 176. | 0,37 | 205. 0,77 |
| 119. | 1,27 | 148. | 1,42 | 177. | -1,33 | 206. 1,10 |
| 120. | 0,62 | 149. | 0,97 | 178. | -1,18 | 207. -1,88 |
| 121. | -1,03 | 150. | 0,62 | 179. | 0,97 | 208. 0,35 |
| 122. | 1,82 | 151. | 0,32 | 180. | 0,70 | 209. 0,92 |
| 123. | 0,42 | 152. | 0,67 | 181. | 1,64 | 210. 1,55 |
| 124. | -2,63 | 153. | 0,77 | 182. | 0,57 | 211. 1,17 |
| 125. | -0,73 | 154. | 0,67 | 183. | 0,24 | 212. 0,67 |
| Продолжение | ||||||
| № сделки P&L | № сделки | P&L | № сделки | P&L | № сделки P&L | |
| 213. 0,82 | 218. | 0,25 | 223. | -1,30 | 228. | 1,80 |
| 214. -0,98 | 219. | 0,14 | 224. | 0,37 | 229. | 2,12 |
| 215. -0,85 | 220. | 0,79 | 225. | -0,51 | 230. | 0,77 |
| 216. 0,22 | 221. | -0,55 | 226. | 0,34 | 231. | -1,33 |
| 217. -1,08 | 222. | 0,32 | 227. | -1,28 | 232. | 1,52 |
Если мы хотим определить приведенное параметрическое оптимальное f, нам придется преобразовать эти торговые прибыли и убытки в процентные повышения и понижения (основываясь на уравнениях с (2.10а) по (2.10в)). Затем мы преобразуем эти процентные прибыли и убытки, умножив их на текущую цену базового инструмента. Например, P&L № 1 составляет 0,18. Допустим, что цена входа в эту сделку была 100,50. Таким образом, процентное повышение по этой сделке будет 0,18/100,50 = 0,001791044776. Теперь предположим, что текущая цена базового инструмента составляет 112,00. Умножив 0,001791044776 на 112,00, мы получаем приведенное P&L = 0,2005970149. Чтобы получить полные приведенные данные, необходимо проделать эту процедуру для всех 232 торговых прибылей и убытков.
Независимо от того, будем мы проводить расчеты, используя приведенные данные, или нет (в этой главе мы не будем использовать приведенные данные), мы все равно должны рассчитать среднее (арифметическое) и стандартное отклонение совокупности этих 232 торговых прибылей и убытков. В нашем случае это 0,330129 и 1,743232 соответственно (если бы мы проводили операции на приведенной основе, нам бы понадобилось определять среднее и стандартное отклонение по приведенным торговым P&L). Теперь мы можем использовать уравнение (3.16), чтобы преобразовать каждую отдельную торговую прибыль и убыток в стандартные единицы.
(3.16) Z=(X-U)/S,
где U = среднее значение данных;
S = стандартное отклонение данных;
Х = наблюдаемая точка данных.
Для сделки № 1 преобразуем прибыль 0,18 в стандартные единицы:
Z= (0,18-0,330129)/1,743232 =-0,150129/1,743232 =-0,08612106708
Таким же образом следующие три сделки -1,11; 0,42 и -0,83 преобразовываются в -0,8261258398; 0,05155423948 и -0,6655046488 стандартных единицы. После того, как мы преобразуем все торговые прибыли и убытки в стандартные единицы, можно собрать в ячейки теперь уже нормированные данные. Вспомните, что при наличии ячеек теряется часть информации о распределении (в нашем случае о распределении отдельных сделок), но характер распределения остается тем же. Допустим, мы помещаем эти 232 сделки в 10 ячеек. Количество ячеек выбрано произвольно — мы могли бы выбрать 9 или 50 ячеек.
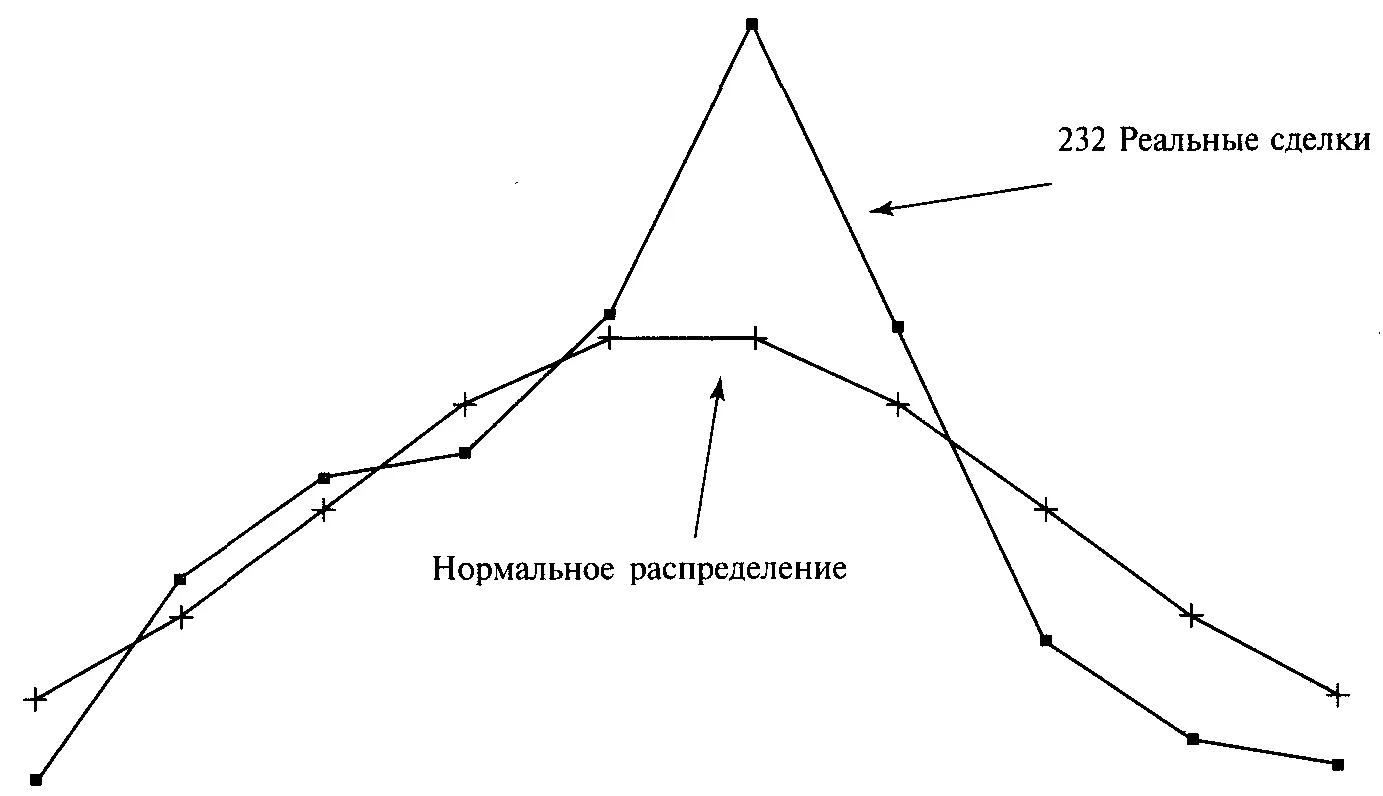
Рисунок3-16 232 сделки в 10 ячейках от -2 до +2 сигмы и нормальное распределение
Когда мы размещаем данные в ячейки, то должны выбрать интервал значений, в котором расположены ячейки. Мы выберем интервал от -2 до +2 сигмы. Это означает, что у нас будет 10 одинаковых ячеек между -2 стандартными единицами и +2 стандартными единицами. Так как между -2 и +2 4 стандартных единицы и мы делим этот диапазон на 10 равных частей, то получаем 4 / 10 = 0,4 стандартных единицы в качестве размера или «ширины» каждой ячейки. Поэтому наша первая ячейка будет содержать те сделки, которые были в диапазоне от -2 до -1,6 стандартных единиц, следующая ячейка будет содержать сделки от-1,6 до-1,2, затем от -1,2 до -0,8, и так далее, пока последняя ячейка не вместит сделки между 1,6 и 2 стандартными единицами. В нашем случае те сделки, которые менее –2 стандартных единиц или больше +2 стандартных единиц, не будут размещены в ячейки, и мы их проигнорируем. Если бы мы пожелали, то включили бы их в крайние ячейки, разместив точки данных менее -2 в ячейку от -2 до -1,6, и таким же образом поступили бы в отношении тех точек данных, которые больше 2. Конечно, мы могли бы выбрать более широкий диапазон, но эти сделки находятся за пределами выбранных ячеек, и мы их не учитываем. Другими словами, мы не рассматриваем сделки, P&L в которых меньше, чем 0,330129 - (1,743232 * 2) = = -3,1563, или больше, чем 0,330129 + (1,743232 * 2) = 3,816593. Мы сейчас создали распределение торговых P&L системы. Распределение содержит 10 точек данных, так как мы решили работать с 10 ячейками. Каждая точка данных отражает число сделок, которые попадают в эту ячейку Каждая сделка не может попасть более чем в 1 ячейку и если сделка находится за пределами 2 стандартных единиц с любой стороны среднего (P&L < -3,156335 или > 3,816593), тогда она не будет представлена в этом распределении. Рисунок 3-16 показывает распределение, которое мы только что рассчитали. Может показаться, что распределение P&L торговой системы должно всегда быть смещено вправо за счет больших выигрышей. Наше распределение 232 торговых P&L представляет систему, которая в основном приносит небольшие прибыли. Многие трейдеры имеют ошибочное мнение, что распределение P&L должно быть смещено вправо для всех торговых систем. Это не всегда верно, что и подтверждает рисунок 3-16. Разные рыночные системы имеют различные распределения, и вам не следует ожидать, что все они будут одинаковыми. Также на рисунке 3-16 показано нормальное распределение для 232 торговых P&L, если бы они были нормально распределены. Это было сделано для того, чтобы вы могли графически сравнить торговые P&L для полученного и нормального распределения. Сначала нормальное распределение рассчитывается для границ каждой ячейки. Для самой левой ячейки это Z =-2 и Z=-1,6. Теперь подставим полученные значения Z в уравнение (3.21), чтобы рассчитать вероятность. В нашем примере это соответствует 0,02275 для Z = -2 и 0,05479932 для Z = -1,6. Затем возьмем абсолютное значение разности этих двух значений, которое в нашем примере будет ABS(0,02275 - 0,05479932) = = 0,03204932. Затем умножим полученный ответ на количество точек данных, то есть на 232 (мы все еще должны использовать 232 сделки, хотя некоторые исключаются, так как находятся вне диапазона выбранных ячеек). Таким образом, если бы данные были нормально распределены и размещены в 10 ячеек равной ширины между -2 и +2 сигма, тогда самая левая ячейка содержала бы 0,03204932 * 232 = 7,43544224 элемента. Если сделать расчет для каждой из 10 ячеек, мы получим нормальную кривую, показанную на рисунке 3-16.
Читать дальшеИнтервал:
Закладка:










