РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров краткое содержание
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
1. Для данного стандартного значения Х рассчитайте его соответствующее N'(X) с помощью уравнения (4.06).
2. Для каждого стандартного значения Х рассчитайте накопленную сумму значений N'(X), соответствующих всем предыдущим X.
3. Теперь, чтобы найти N(X), т.е. итоговую вероятность для данного X, прибавьте текущую сумму, соответствующую значению X, к текущей сумме, соответствующей предыдущему значению X. Разделите полученную величину на 2. Затем разделите полученное частное на общую сумму всех N'(X), т.е. последнее число в столбце текущих сумм. Это новое частное является ассоциированной 1-хвостой вероятностью для данного X.
Так как теперь у нас есть метод поиска ассоциированных вероятностей для стандартных значений Х при данном наборе значений параметров, мы можем найти оптимальное f. Процедура в точности совпадает с той, которая применяется для поиска оптимального f при нормальном распределении. Единственное отличие состоит в том, что мы рассчитываем столбец ассоциированных вероятностей другим способом. В нашем примере с 232 сделками значения параметров, которые получаются при самом низком значении статистики К-С, составляют 0,02, 2,76, О и 1,78 для LOC, SCALE, SKEW и KURT соответственно. Мы получили эти значения параметров, используя процедуру оптимизации, описанную в данной главе. Статистика К-С == 0,0835529 (это означает, что в своей наихудшей точке два распределения удалены на 8,35529%) при уровне значимости 7,8384%. Рисунок 4-10 показывает функцию распределения для тех значений параметров, которые наилучшим образом подходят для наших 232 сделок. Если мы возьмем полученные параметры и найдем оптимальное f по этому распределению, ограничивая распределение +3 и -3 сигма, используя 100 равноотстоящих точек данных, то получим f= 0,206, или 1 контракт на каждые 23 783,17 доллара. Сравните это с эмпирическим методом, который покажет, что оптимальный рост достигается при 1 контракте на каждые 7918,04 доллара на балансе счета. Этот результат мы получаем, если ограничиваем распределение 3 сигма с каждой стороны от среднего. В действительности, в эмпирическом потоке сделок у нас был проигрыш наихудшего случая 2,96 сигма и выигрыш наилучшего случая 6,94 сигма. Теперь, если мы вернемся и ограничим распределение 2,96 сигма слева от среднего и 6,94 сигма справа (и на этот раз будем использовать 300 равноотстоящих точек данных), то получим оптимальное f = 0,954, или 1 контракт на каждые 5062,71 доллара на балансе счета. Почему оно отличается от эмпирического оптимального f= 7918,04?
Проблема состоит в «грубости» фактического распределения. Вспомните, что уровень значимости наших наилучшим образом подходящих параметров был только 7,8384%. Давайте возьмем распределение 232 сделок и поместим в 12 ячеек от -3 до +3 сигма.
| Ячейки | Количество сделок | |
| -3,0 | -2,5 | 2 |
| -2,5 | -2,0 | 1 |
| -2,0 | -1,5 | 2 |
| -1,5 | -1,0 | 24 |
| -1,0 | -0,5 | 39 |
| ,sr„. -0,5 | 0,0 | 43 |
| ь -' 0,0 | 0,5 | 69 |
| 0,5 | 1,0 | 38 |
| 1,0 | 1,5 | 7 |
| 1,5 | 2,0 | 2 |
| 2,0 | 2,5 | 0 |
| 2,5 | 3,0 | 2 |
Отметьте, что на хвостах распределения находятся пробелы, т.е. области, или ячейки, где нет эмпирических данных. Эти области сглаживаются, когда мы приспосабливаем наше регулируемое распределение к данным, и именно эти сглаженные области вызывают различие между параметрическим и эмпирическим оптимальным f. Почему же наше характеристическое распределение при всех возможностях регулировки его формы не очень хорошо приближено к фактическому распределению? Причина состоит в том, что наблюдаемое распределение имеет слишком много точек перегиба. Параболу можно направить ветвями вверх или вниз. Однако вдоль всей параболы направление вогнутости или выпуклости не изменяется. В точке перегиба направление вогнутости изменяется. Парабола имеет 0 точек перегиба, 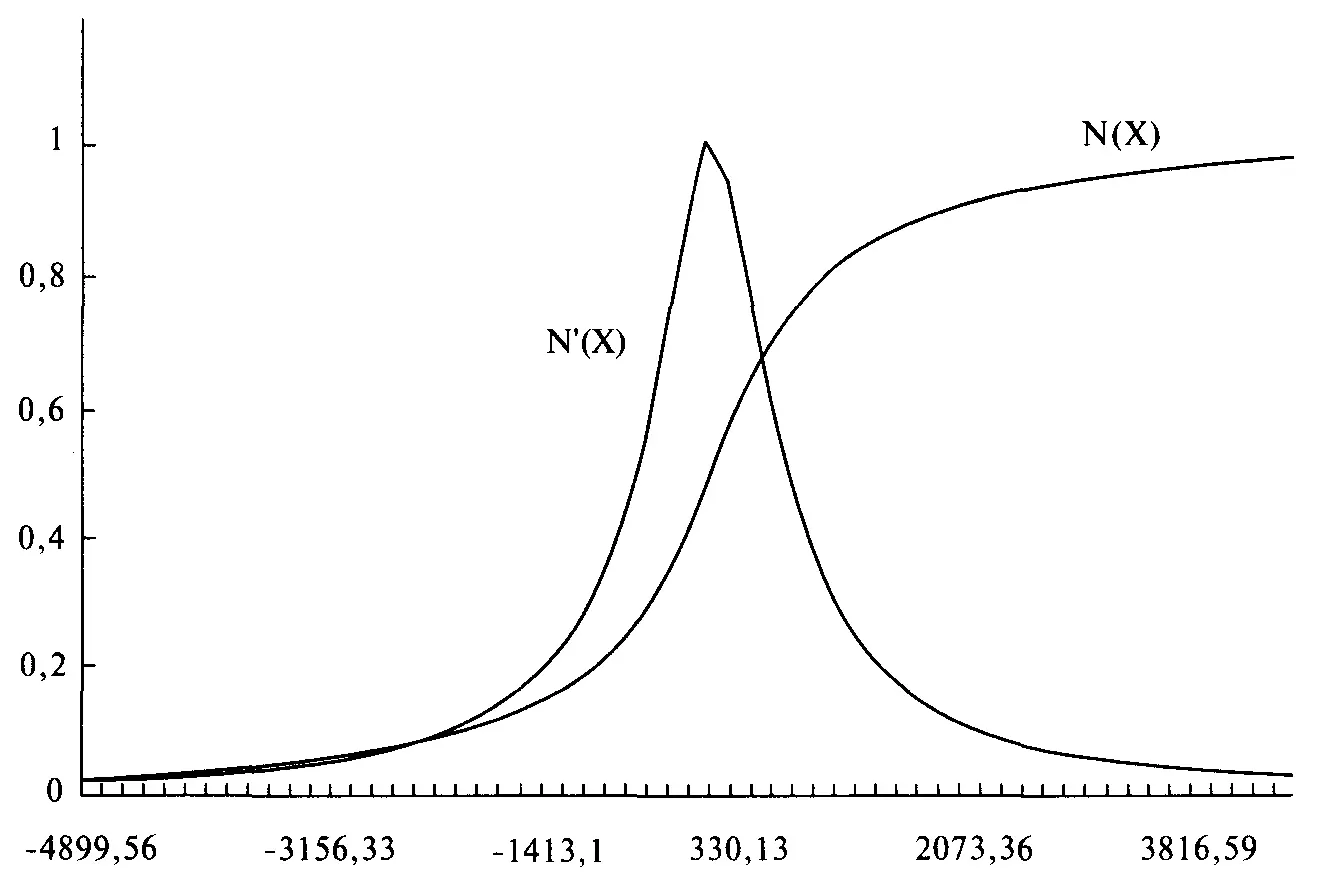
Рисунок 4-10Регулируемое распределение для 232 сделок
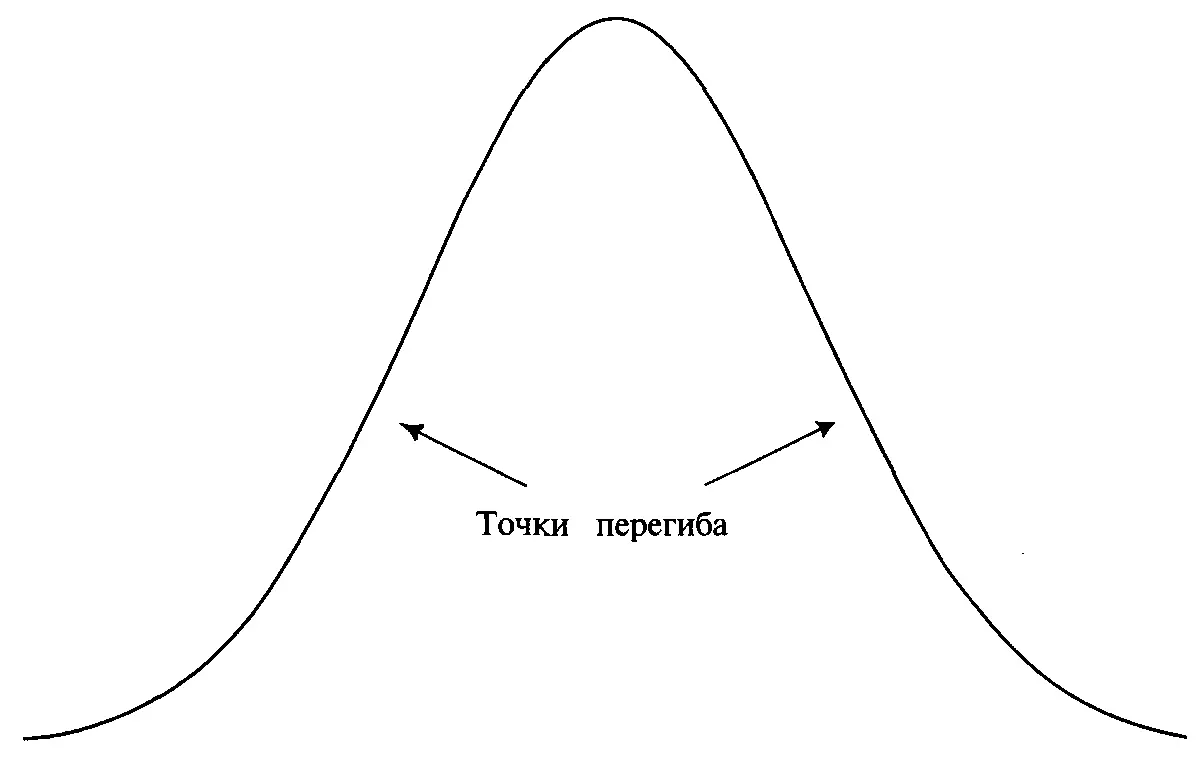
Рисунок 4-11Точки перегиба колоколообразного распределения
так как направление вогнутости никогда не изменяется. Объект, имеющий форму буквы S, лежащий на боку, имеет одну точку перегиба, т.е. точку, где вогнутость изменяется. Рисунок 4-11 показывает нормальное распределение. Отметьте, что в колоколообразной кривой, такой как нормальное распределение, есть две точки перегиба. В зависимости от значения SCALE наше регулируемое распределение может иметь ноль точек перегиба (если SCALE очень низкое) или две точки перегиба. Причина, по которой наше регулируемое распределение не очень хорошо описывает фактическое распределение сделок, состоит в том, что реальное распределение имеет слишком много точек перегиба. Означает ли это, что полученное характеристическое распределение неверно? Скорее всего нет. При желании мы могли бы создать функцию распределения, которая имела бы больше двух точек перегиба. Такую функцию можно было бы лучше подогнать к реальному распределению. Если бы мы создали функцию распределения, которая допускает неограниченное количество точек перегиба, то мы бы точно подогнали ее к наблюдаемому распределению. Оптимальное f, полученное с помощью такой кривой, практически совпало бы с эмпирическим. Однако чем больше точек перегиба нам пришлось бы добавить к функции распределения, тем менее надежной она была бы (т.е. она хуже представляла бы будущие сделки). Мы не пытаемся в точности подогнать параметрическое ik наблюдаемому, а стараемся лишь определить, как распределяются наблюдаемые данные, чтобы можно было предсказать с большой уверенностью будущее оптимальное 1(если данные будут распределены так же, как в прошлом). В регулируемом распределении, подогнанном к реальным сделкам, удалены ложные точки перегиба.
Поясним вышесказанное на примере. Предположим, мы используем доску Галтона. Мы знаем, что асимптотически распределение шариков, падающих через доску, будет нормальным. Однако мы собираемся бросить только 4 шарика. Можем ли мы ожидать, что результаты бросков 4 шариков будут распределены нормально? Как насчет 5 шариков? 50 шариков? В асимптотическом смысле мы ожидаем, что наблюдаемое распределение будет ближе к нормальному при увеличении числа сделок. Подгонка теоретического распределения к каждой точке перегиба наблюдаемого распределения не даст нам большую степень точности в будущем. При большом количестве сделок мы можем ожидать, что наблюдаемое распределение будет сходиться с ожидаемым и многие точки перегиба будут заполнены сделками, когда их число стремится к бесконечности. Если наши теоретические параметры точно отражают распределение реальных сделок, то оптимальное f, полученное на основе теоретического распределения, при будущей последовательности сделок будет точнее, чем оптимальное f, рассчитанное эмпирически из прошлых сделок. Другими словами, если наши 232 сделки представляют распределение сделок в будущем, тогда мы можем ожидать, что распределение сделок в будущем будет ближе к нашему «настроенному» теоретическому распределению, чем к наблюдаемому, с его многочисленными точками перегиба и «зашумленностью» из-за конечного количества сделок. Таким образом, мы можем ожидать, что будущее оптимальное f будет больше похоже на оптимальное f, полученное из теоретического распределения, чем на оптимальное f, полученное эмпирически из наблюдаемого распределения.
Читать дальшеИнтервал:
Закладка:










