РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров

Проведение тестов «что если»

После того как найдено параметрическое оптимальное f, можно реализовывать сценарии «что если» с помощью полученной функции распределения. Для этого нужно варьировать параметры функции распределения LOC, SCALE, SKEW и KURT для моделирования различных ожидаемых результатов (различных рас­пределений, которые могут быть в будущем). Мы знаем, как применять проце­дуру растяжения и сжатия в нормальном распределении, и похожим образом можем работать с параметрами LOC, SCALE, SKEW и KURT регулируемого распределения.

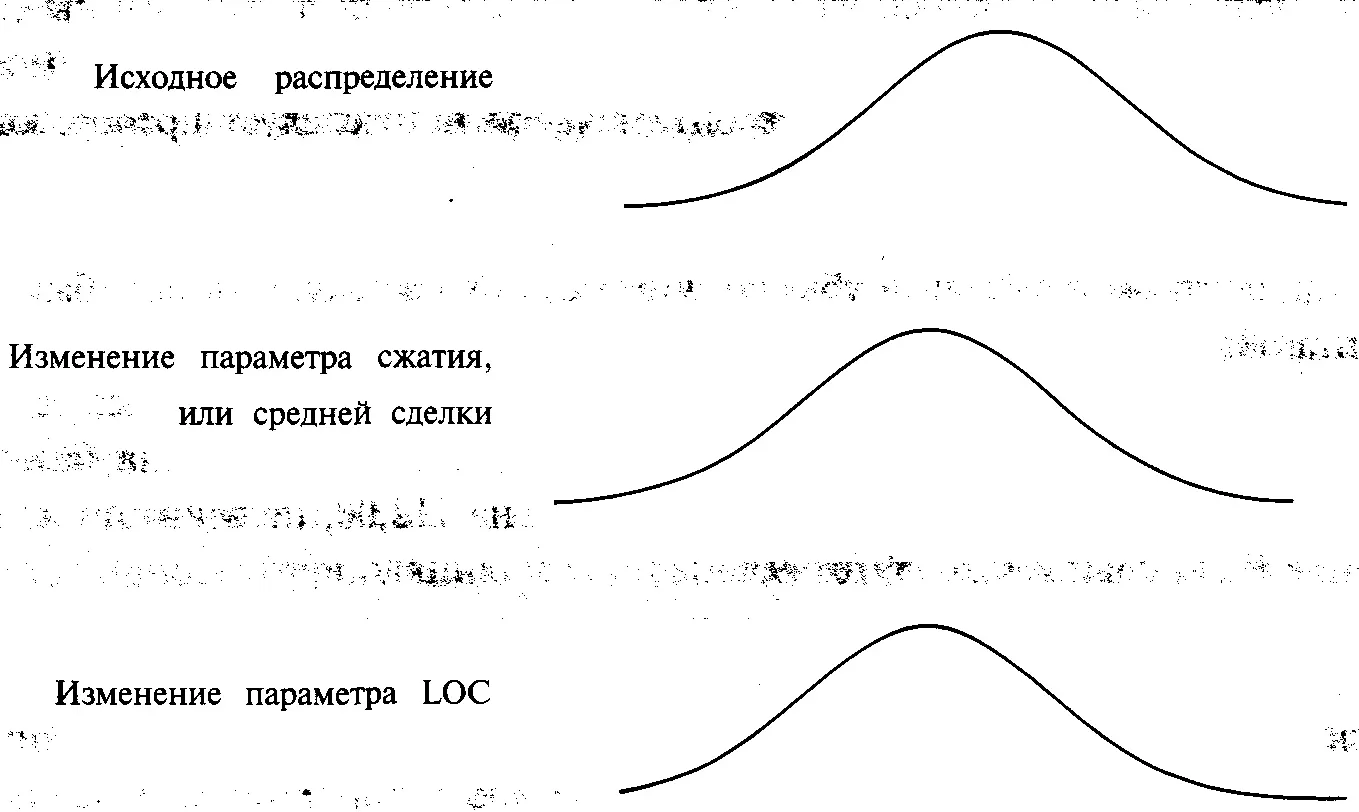
Рисунок 4-12Изменение параметра расположения распределения

Сценарии «что если» при параметрическом подходе помогают смоделировать из­менения фактического распределения торговых P&L. Параметрические методы позволяют увидеть воздействие изменений на распределение фактических торго­вых прибылей и убытков до того, как они произойдут.

Когда вы работаете с параметрами, следует помнить о важной детали. При поис­ке оптимального f вместо того, чтобы изменять LOC, т.е. расположение распределе­ния, лучше изменять долларовую арифметическую среднюю сделку, используемую в качестве входного данного. Это видно из рисунка 4-12. Отметьте (см. рисунок 4-12), что изменение параметра расположения LOC передвигает распределение вправо или влево в «окне» ограничительных пара­метров, но сами ограничительные параметры при этом не двигаются. Таким образом, изменение параметра LOC также затрагивает количество равноотсто­ящих точек данных слева и справа от моды распределения. Если изменить фактическое среднее арифметическое (или использовать переменную сжатия при поиске f в нормальном распределении), «окно» ограничительных пара­метров передвинется. Когда вы изменяете арифметическую среднюю сделку или изменяете переменную сжатия в механизме нормального распределения, у вас остается то же число равноотстоящих точек данных справа и слева от моды распределения.

Приведение f к текущим ценам

В методе, описанном в этой главе, были использованы неприведенные данные. Мы можем использовать тот же подход для приведенных данных. Если необходимо оп­ределить приведенное параметрическое оптимальное f, то следует преобразовать необработанные торговые прибыли и убытки в процентные повышения и пониже­ния, основываясь на уравнениях с (2.10а) по (2.10в). Затем надо преобразовать по­лученные процентные прибыли и убытки, умножив их на текущую цену базового инструмента. Например, P&L номер 1 составляет 0,18. Допустим, что цена входа в этой сделке равна 100,50, тогда процентное повышение для этой сделки рав­но 0,18/100,50=0,001791044776. Теперь допустим, что текущая цена базового инструмента равна 112,00. Умножив 0,001791044776 на 112,00, получим приведен­ное значение P&L, равное 0,2005970149. Если мы хотим использовать приведенные данные, то следует провести анало­гичную операцию со всеми 232 торговыми прибылями и убытками. Затем следует рассчитать среднее арифметическое и стандартное отклонение по приведенным сделкам и использовать уравнение (3.16) для нормирования данных. Далее необ­ходимо найти набор оптимальных параметров LOC, SCALE, SKEW и KURT по приведенным данным так же, как было показано в этой главе для неприведенных данных. Процедура определения оптимального f, среднего геометрического и TWR аналогична уже рассмотренной нами. Побочные продукты: средняя геометрическая сделка, средняя арифметическая сделка и порог геометри­ческой торговли — действительны только для текущей цены базового инструмен­та. Если цена базового инструмента изменится, расчет следует повторить, вернув­шись к первому шагу, умножив процентные прибыли и убытки на новую цену базового инструмента. Когда вы перейдете к этой процедуре с другой ценой базово­го инструмента, то получите такое же оптимальное f, среднее геометрическое и TWR. Однако средняя арифметическая сделка, средняя геометрическая сделка и порог геометрической торговли будут другими в зависимости от новой цены базо­вого инструмента.

Количество контрактов для торговли, определяемое уравнением (3.34), также должно измениться. Ассоциированное P&L наихудшего случая (переменная W из уравнения (3.35)) будет другим в уравнении (3.34) в результате изменений, выз­ванных приведением данных к другой текущей цене.

Оптимальное F для других распределений и настраиваемых кривых

Существует много других способов, с помощью которых можно определить параметрическое оптимальное f. В предыдущей главе мы рассмотрели проце­дуру поиска оптимального f для нормально распределенных данных. Итак, у нас есть процедура, которая дает оптимальное f для любого нормально распре­деленного явления. Та же процедура используется для поиска оптимального/в любом распределении, если существует функция распределения (подобные функ­ции описаны для многих других распространенных распределений в приложе­нии В). Когда функции распределения не существует (т.е. когда функция плот­ности вероятности не интегрируется), оптимальное f можно найти с помощью численного метода, описанного в этой главе, приблизительно рассчитав функцию распределения.

Данная глава посвящена моделированию фактического распределения сделок с помощью регулируемого распределения, то есть поиску функции и ее подходя­щих параметров, которые моделируют фактическую функцию плотности вероят­ности торговых P&L с двумя точками перегиба. Вы можете использовать уже из­вестные функции и методы, например, полиномиальную интерполяцию или эк­страполяцию, интерполяцию и экстраполяцию рациональной функции (частные многочленов), или использовать сплайн-интерполяцию. После того как теорети­ческая функция найдена, можно определить ассоциированные вероятности тем же методом расчета интеграла, который использовался при поиске ассоцииро­ванных вероятностей регулируемого распределения, или рассчитать интеграл с помощью методов математического анализа. Одна из целей этой книги — позволить трейдерам, использующим немеха­нические системы, применять те же методы управления счетом, что и трейде­рам, использующим механические системы. Регулируемое распределение тре­бует расчета параметров, они относятся к первым четырем моментам распре­деления. Именно эти моменты — расположение, масштаб, асимметрия и экс­цесс — описывают распределение. Таким образом, кто-либо, торгующий по немеханическому методу, например по волнам Эллиотта, может рассчитать параметры и получить оптимальное f и побочные продукты. Наличие прошлой истории сделок не является необходимым условием для расчета данных пара­метров. Если бы вы использовали другие упомянутые выше методы подгонки, вам также не обязательно было бы знать исторические данные, но значения параметров такой подгонки не обязательно относились бы к моментам рас­пределения. Эти методы могут лишить вас возможности посмотреть, что про­изойдет, если увеличится эксцесс или изменится асимметрия, изменится мас­штаб и т.д. Наше регулируемое распределение является логичным выбором теоретической функции, которая хорошо описывает фактическое распределе­ние, так как параметры не только задают моменты распределения, они дают нам контроль над этими моментами при прогнозировании будущих измене­ний в распределении. Более того, рассчитать параметры рассматриваемого здесь регулируемого распределения легче, чем подогнать какую-либо произ­вольную функцию.