РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров краткое содержание
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Количество, рассмотренное здесь, является количеством денег, но это могут быть не только деньги, и метод будет работать. Данный подход можно использовать для любого количественного решения в среде благоприятной неопределенности .
Если вы создадите различные сценарии для фондового рынка, оптимальное f. полученное с помощью этого метода, даст вам процент средств, которые надо в данный момент инвестировать в акции. Например, если f= 0,65, то 65% вашего баланса должно быть на рынке, а оставшиеся 35%, например, в деньгах. Этот подход даст вам наибольший геометрический рост капитала. Конечно, результат будет зависеть от того, какие входные данные вы использовали в системе (сценарии. их вероятности осуществления, выигрыши и проигрыши, издержки). Все сказанное ранее об оптимальном f применимо здесь, и это означает также, что ожидаемые проигрыши могут достигать 100%. Если вы осуществляете планирование сценария для размещения активов, то должны ожидать, что около 100% активов. размещенных в соответствии с рассматриваемым сценарием, могут быть потеряны в какое-либо время в будущем. Например, вы используете данный метод, чтобы определить сумму средств, предназначенных для инвестирования в акции. Допустим, вы приходите к выводу, что 65% средств должно быть инвестировано в акции, а оставшиеся 35% в безрисковые активы. Следует ожидать, что проигрыш в будущем может достичь 100% суммы, размещенной на фондовом рынке. Другими словами, вы должны быть готовы, что в какой-либо точке в будущем почти 100% активов от ваших 65%, размещенных в акции, будут проиграны. Однако именно таким образом вы достигнете максимального геометрического роста. Ту же процедуру можно использовать для альтернативного параметрического метода определения оптимального f в торговле. Допустим, вы принимаете торговые решения, основываясь на фундаментальных данных. Вы намечаете различные сценарии, которые могут произойти в процессе торговли. Чем больше сценариев и чем точнее сценарии, тем лучше будут полученные результаты. Предположим, вы решили купить муниципальные облигации, но при этом не планируете удерживать их до срока погашения. Вы можете рассмотреть множество сценариев будущих событий и использовать эти сценарии для определения оптимального размера инвестиций.
Концепцию планирования сценария для определения оптимального f можно использовать во многих областях: от военных стратегий до определения оптимального уровня участия в подписке на акции или оптимальной предоплаты за дом. Этот метод, вероятно, является лучшим и уже точно самым легким для тех, кто не использует механические решения при входе и выходе с рынка. Трейдеры, которые торгуют по фундаментальным данным, графикам, волнам Эллиотта или с помощью любого другого метода, требующего субъективного суждения, могут найти оптимальные f с помощью этого подхода — он намного проще, чем поиск значений параметров распределения. Арифметическое среднее HPR группы сценариев можно рассчитать следующим образом:
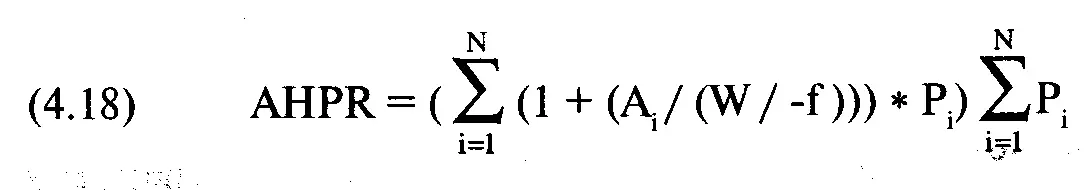
где N = число сценариев;
А = результат (выигрыш или проигрыш) сценария i;
Р = вероятность сценария i;
W= наихудший результат среди всех сценариев.
AHPR будет важно позднее, при поиске эффективной границы совокупности нескольких рыночных систем, когда необходимо будет определить ожидаемую прибыль (арифметическую) данной рыночной системы. Эта ожидаемая прибыль равна AHPR-1. Рассмотренный метод не обязательно должен быть основан на параметрическом подходе. Возможен и эмпирический подход. Другими словами, мы можем взять отчет о сделках данной рыночной системы и использовать каждую из этих сделок в качестве сценария, который может произойти в будущем. Величина прибыли или убытка будет выходным результатом данного сценария. В этом случае каждый сценарий (сделка) имеет равную вероятность осуществления — 1/N, где N — общее число сделок (сценариев). В результате мы получим эмпирическое оптимальное f. Когда есть несколько решений на основе нескольких сценариев, выбор того. чье среднее геометрическое, соответствующее оптимальному f, самое большое. максимизирует решение в асимптотическом смысле. Зачастую это будет происходить вопреки общепринятым правилам принятия решения, таким как Правило Гурвица, максимакс, минимакс, минимаксная потеря (minimax regret) и наивысшее математическое ожидание. Предположим, мы должны выбрать одно их двух возможных решений, которые назовем «белым» и «черным». Белое решение представляет следующие возможные сценарии:
| Белое решение | ||
| Сценарий | Вероятность | Результат |
| А | 0,3 | -20 |
| В | 0,4 | 0 |
| С | 0,3 | 30 |
| Математическое | ожидание = $3,00 | |
| Оптимальное f = | 0, 17 | |
| Среднее геометрическое = 1,0123 |
Черное решение представляет следующие сценарии:
| Черное решение | ||
| Сценарий | Вероятность | Результат |
| А | 0,3 | -10 |
| В | 0,4 | 5 |
| С | 0,15 | 6 |
| D | 0,15 | 20 |
Математическое ожидание = $2,90
Оптимальное f=0,31
Среднее геометрическое = 1,0453
Многие выбрали бы белое решение, так как оно имеет большее математическое ожидание. При белом решении вы можете ожидать «в среднем» выигрыш в 3 доллара против выигрыша черного решения в 2,90 доллара. Однако выбор черного решения будет более правильным, так как оно дает наибольшее среднее геометрическое. При черном решении можно ожидать «в среднем» выигрыш в 4,53% (1,0453 - 1) против выигрыша белого решения в 1,23%. При реинвестировании черное решение, в среднем, выиграет в три раза больше, чем белое решение! Вы можете возразить, отметив, что мы не реинвестируем по тому же сценарию каждый раз, и можно добиться большего, если всегда выбирать наивысшее арифметическое математическое ожидание для каждого представленного набора. Мы будем принимать решение, основываясь на большем арифметическом математическом ожидании, только в том случае, если не собираемся реинвестировать вообще. Но так как почти всегда деньги, которыми мы рискуем сегодня, будут снова с риском вложены в будущем, а деньги, выигранные или проигранные в прошлом, влияют на то, чем мы можем рисковать сегодня (среда геометрических следствий), для максимизации долгосрочного роста капитала мы должны принимать решения, исходя из среднего геометрического. Даже если сценарии, которые будут представлены завтра, не будут такими же, как сегодня, используя наибольшее среднее геометрическое, мы всегда максимизируем наши решения. Это аналогично процессу зависимых попыток, например игре в «очко». Каждая раздача изменяет вероятности, поэтому оптимальная ставка изменяется, чтобы максимизировать долгосрочный рост. Помните, чтобы максимизировать долгосрочный рост, мы должны рассматривать текущую игру как неограниченную во времени. Другими словами, следует рассматривать каждую отдельную ставку, как будто она повторяется бесконечное число раз, если необходимо максимизировать рост в течение долгой последовательности ставок в нескольких играх. Давайте обобщим все вышесказанное: когда результат события оказывает влияние на результат(ы) последующего события(ий), нам следует выбирать наибольшее геометрическое ожидание. В редких случаях, когда результат не влияет на последующие события, следует выбирать наибольшее арифметическое ожидание. Математическое ожидание (арифметическое) не учитывает зависимость результатов внутри каждого сценария и поэтому может привести к неверному заключению, когда рассматривается реинвестирование в геометрической среде. Использование предложенного метода в планировании сценария поможет вам правильно выбрать сценарий, оценить его результаты и вероятности их осуществления. Этот метод внутренне более консервативен, чем размещение на основе наибольшего арифметического математического ожидания. Уравнение (3.05) показывает, что среднее геометрическое никогда не может быть больше среднего арифметического. Таким образом, этот метод никогда не будет более рискованным, чем метод наибольшего арифметического математического ожидания. В асимптотическом смысле (долгосрочном) это не только лучший метод размещения, так как вы получаете наибольший геометрический рост, он также более безопасен, чем размещение по наибольшему арифметическому математическому ожиданию, которое неизменно смещает вас вправо от пика кривой f .
Читать дальшеИнтервал:
Закладка:










