Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

История водорослей в озере подчеркивает, что наша неспособность мыслить экспоненциально может вызывать разрушение экосистем и популяций. Разумеется, в списке видов, находящихся под угрозой исчезновения, находится и наш собственный – несмотря на ясные и непрекращающиеся тревожные звоночки.

В период между 1347 и 1351 годами «черная смерть» [32] «Черная смерть» или «черный мор» – пандемия бубонной чумы 1347–1357 гг. – Прим. ред. , одна из самых разрушительных пандемий в истории человечества (распространение инфекционных заболеваний мы подробнее рассмотрим в главе 7), захлестнула Европу, уничтожив 60 % ее населения. В результате общая численность человечества сократилась примерно до 370 миллионов человек. С тех пор население мира росло постоянно, без спадов. К 1800 году количество людей достигло почти миллиарда. Очевидный быстрый рост численности населения в тот период побудил английского математика Томаса Мальтуса предположить, что человеческое население растет пропорционально его текущему размеру [33] Мальтус, Т. «Опыт о законе народонаселения». Пер. П. А. Бибикова. По изданию: Мальтус Т. Р. Опыт о законе народонаселения. – СПб., 1868. ДиректМедиа Паблишинг – М., 2008. . Как и в случае с клетками в эмбрионе на раннем этапе развития или деньгами, остающимися нетронутыми на банковском счете, это простое правило предполагает экспоненциальный рост человечества на уже перенаселенной планете.

Излюбленным сюжетом многих научно-фантастических романов и фильмов (например, недавних блокбастеров «Интерстеллар» и «Пассажиры») является решение проблем перенаселения Земли за счет освоения космоса. Там, как правило, обнаруживается похожая на Землю подходящая планета, которой суждено стать новым домом для неудержимо растущей человеческой расы. Но такой поворот – вовсе не прерогатива буйной фантазии писателей и сценаристов: в 2017 году выдающийся ученый Стивен Хокинг обосновал перспективы колонизации космоса. Он предупредил, что, если наш вид хочет пережить угрозу вымирания, вызванную перенаселением и связанными с ним климатическими изменениями, люди должны в ближайшие 30 лет начать колонизацию Марса или Луны. Однако, к сожалению, если темпы роста населения Земли не снизятся, то даже переправив половину нынешних ее жителей на новую планету земного типа, мы обеспечим человечеству всего лишь 63 года жизни. Потом общая численность землян вновь удвоится, и обе планеты достигнут предела плотности населения. Мальтус, писавший: «Одного населения Земли было бы достаточно, чтобы в несколько тысячелетий покрыть миллионы миров», – предсказывал, что экспоненциальный рост обессмыслит идею межпланетной колонизации.

Однако, как мы уже выяснили (вспомним бактерии стрептококка группы D, растущие в молочной бутылке в начале этой главы), экспоненциальный рост не может продолжаться вечно. Как правило, по мере роста численности населения ресурсы окружающей среды, которая его поддерживает, истощаются, а чистые темпы роста (разница между рождаемостью и смертностью) естественным образом снижаются. Считается, что окружающая среда обладает конечной несущей способностью для каждого конкретного вида – присущим ей максимальным пределом устойчивости популяции. Дарвин полагал, что ограничения, налагаемые природной средой, вызовут «борьбу за существование», поскольку отдельные особи «будут конкурировать за свое место в экономике природы». Простейшая математическая модель, позволяющая отразить последствия внутри– или межвидовой конкуренции за ограниченные ресурсы, называется моделью логистического роста.

На рис. 3 логистический рост поначалу выглядит экспоненциальным, поскольку население свободно растет пропорционально своим текущим размерам, без ограничений условиями окружающей среды. Однако по мере роста населения нехватка ресурсов приближает уровень смертности к уровню рождаемости. Чистый прирост населения в итоге сводится к нулю: новых рождений среди населения достаточно только для того, чтобы заменить умерших и не более, что означает, численность населения достигает плато своего предельного воспроизводства.

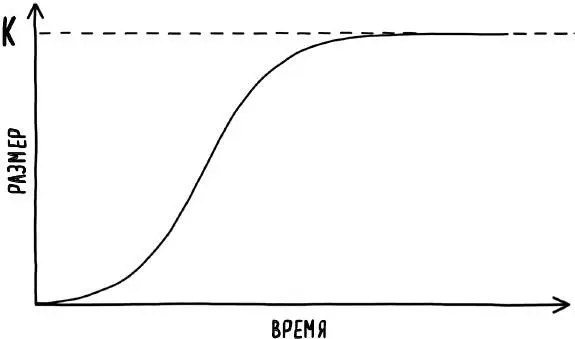
Рис. 3. Сначала кривая логистического роста увеличивается почти по экспоненте, но затем, по мере истощения ресурсов, рост замедляется, а население приближается к предельному размеру «К»

Шотландский ученый Андерсон Маккендрик (один из первых математических биологов, с которым мы познакомимся в главе 7 в контексте его работы по моделированию распространения инфекционных заболеваний) первым продемонстрировал, что в популяциях бактерий происходит логистический рост [34] McKendrick, A. G., & Pai, M. K. (1912). The rate of multiplication of micro-organisms: a mathematical study. Proceedings of the Royal Society of Edinburgh, 31, 649–53. https://doi.org/10.1017/S0370164600025426 . Последующие исследования подтвердили, что логистическая модель прекрасно описывает поведение популяции в новой среде на таких разнообразных примерах, как овцы [35] Davidson, J. (1938). On the ecology of the growth of the sheep population in South Australia. Trans. Roy. Soc. S. A., 62 (1), 11–148. Davidson, J. (1938). On the growth of the sheep population in Tasmania. Trans. Roy. Soc. S. A., 62 (2), 342–6. , тюлени [36] Jeffries, S., Huber, H., Calambokidis, J., & Laake, J. (2003). Trends and status of harbor seals in Washington State: 1978–1999. The Journal of Wildlife Management, 67 (1), 207. https://doi.org/10.2307/3803076 и журавли [37] Flynn, M. N., & Pereira, W. R. L. S. (2013). Ecotoxicology and environmental contamination. Ecotoxicology and Environmental Contamination, 8 (1), 75–85. .

Потенциальный предельный размер популяции многих видов животных остается примерно постоянной величиной, так как зависит от ресурсов в их среде обитания. Человек же оказался способен постоянно увеличивать пределы своей популяции благодаря множеству факторов, в числе которых – промышленная революция, механизация сельского хозяйства и Зеленая революция [38] Третья сельскохозяйственная революция – комплекс изменений в сельском хозяйстве развивающихся стран в 1940–1970 годах, который привел к значительному увеличению мировой сельскохозяйственной продукции. – Прим. ред. . Хотя в настоящее время оценки пределов устойчивого народонаселения Земли различаются, многие исследования показывают, что эти пределы составляют от девяти до десяти миллиардов человек. Известный социобиолог Эдвард Озборн Уилсон считает, что биосфера Земли способна поддержать существование лишь жестко ограниченного количества населения [39] Wilson, E. O. (2002). The Future of Life (1st ed.). Alfred A. Knopf. . В число сдерживающих факторов включают наличие пресной воды, ископаемого топлива и других невозобновляемых ресурсов, условия окружающей среды (прежде всего, изменение климата) и жизненное пространство. Чаще всего исследователи обращают внимание на проблему пропитания. По оценкам Уилсона, даже если бы все стали вегетарианцами, питаясь произведенной пищей напрямую, а не скармливая ее скоту (поскольку поедание животных является неэффективным способом преобразования энергии растений в продовольственную энергию), нынешних 1,4 миллиарда гектаров пахотных земель хватало бы для того, чтобы прокормить с них лишь десять миллиардов человек.