М. Нсанов - Цифровые устройства. Учебник для колледжей

Запишем СДНФ для заданной в табл.2.1 логической функции Y 1на рис.2.1.

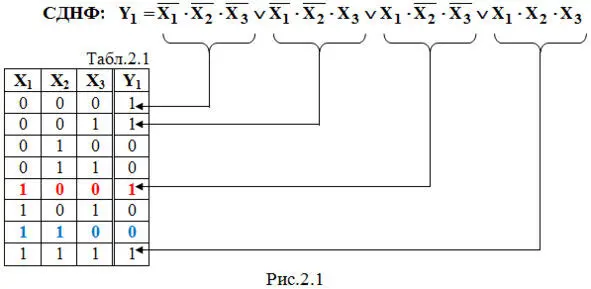
Приведем еще два примера составления СДНФ для логических функций Y 2и Y 3, заданных в табл.2.2 на рис.2.2.

2. СКНФ (совершенная конъюнктивная нормальная форма) представляет собой несколько многочленов (минтермов), объединенных операцией логического умножения (конъюнкции), почему форма и названа конъюнктивной. Она составляется для значений функции Y, равных 0 , количество которых и определяет число многочленов. Каждый многочлен представляет собой логическое сложение всех переменных (в данном случае – трех переменных Х 1, Х 2, Х 3), причем для значения любой переменной X = 1 следует брать ее инверсию.

Запишем СКНФ для заданной в табл.2.1 логической функции Y 1(на рис.2.3).

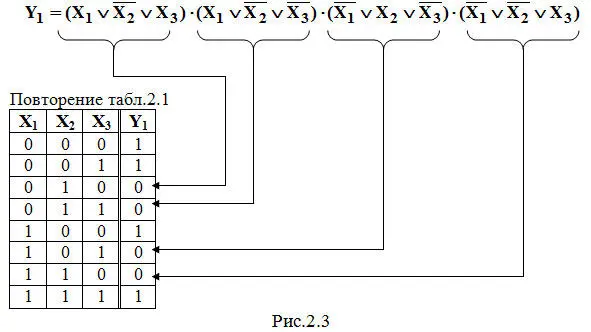
П р и м е ч а н и е:

Символом операции НЕ (инвертирования) обычно является черточка над буквой, как показано в табл.1.1. Именно такой символ мы применяли при записи СДНФ для функций Y 1, Y 2, Y 3и СКНФ для функции Y1. Но довольно часто, особенно на рисунках карт Вейча (Карно) и в изображениях микросхем, используется другой символ инвертирования – апостроф рядом с буквой: Y = X′. Как уже упоминалось во Введении, при выполнении лабораторных работ, а также в демонстрационных материалах применяется компьютерная программа исследования работы элементов и устройств цифровой микроэлектроники Electronics Workbench, где для изображения инверсных выводов как раз употребляется второй вариант символа инвертирования. Поэтому в дальнейшем для привыкания мы будем практиковать оба варианта символа инвертирования.

Приведем еще два примера записи СКНФ для функций Y 2и Y 3, заданных в табл.2.2, где будем использовать два варианта записи символа инвертирования (рис.2.4):

В дальнейшем мы будем применять апостроф преимущественно в текстовом материале и формулах, а черточку над буквами – на рисунках.

Любая совершенная нормальная форма (СДНФ или СКНФ) содержит очень большое количество логических операций, поэтому схемная реализация ЦУ непосредственно по СДНФ (или по СКНФ) потребует соответствующего числа логических элементов, которые должны будут выполнять данные операции. Поэтому невольно напрашивается вопрос: а нельзя ли логические выражения вида СДНФ или СКНФ упростить, чтобы количество операций (и, соответственно, количество элементов в схеме ЦУ) стало меньше? Оказывается, что в подавляющем большинстве случаев это сделать можно!

Процесс упрощения логических выражений любой совершенной нормальной формы записи получил название: минимизация от латинского minimum. Существует несколько способов ручной минимизации, но практически наиболее простым и наглядным является метод Вейча (несколько модифицированный метод Карно ), который мы и будем здесь рассматривать. Его единственным недостатком является невозможность применения для минимизации логических выражений, содержащих более чем 5 переменных; но т.к. это случается довольно редко, то с указанным недостатком вполне можно мириться.

Сущность данного метода заключается в применении так называемых карт (диаграмм) Вейча, которые представляют собой прямоугольники, разделенные на клетки (карты Карно несколько отличаются от карт Вейча, но суть метода та же; – смотрите окончание данного параграфа). Количество клеток в карте определяется числом наборов переменных (числом комбинаций входных сигналов) N = 2 n, где n – это количество переменных; причем каждой клетке строго соответствует свой набор переменных, определяемый по обычной координатной сетке.

Рассмотрим два наиболее часто встречающихся случая:

1. Для ЦУ с n = 3 входами максимальное число наборов переменных (смотрите таблицы 2.1 и 2.2 таких устройств) равно 2 n= 2 3 = 8, следовательно и карта Вейча будет иметь 8 клеток (рис.2.5):

2. Для ЦУ, имеющего n = 4 входа, максимальное число наборов переменных равно 2 n= 2 4 = 16, поэтому карта Вейча тоже будет иметь 16 клеток (рис.2.6).

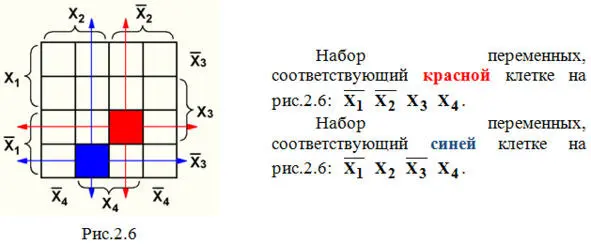
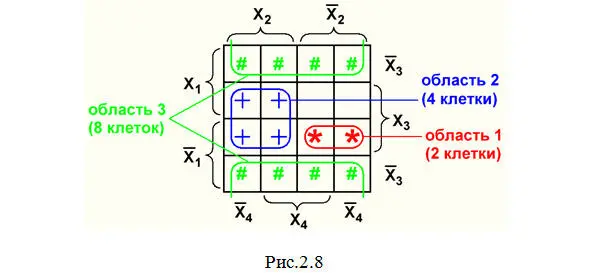
Главной особенностью любой карты Вейча является возможность объединения соседних клеток карты. Области объединения должны быть прямоугольными и содержать 2 n(2,4,8,16) клеток. Допускается сворачивать карту в цилиндр с объединением соседних граней; примерами такого объединения являются: область 1 на рис.2.7 и область 3 на рис.2.8. Не допускается включать в объединение пустые клетки.

Рассмотрим примеры объединения клеток.

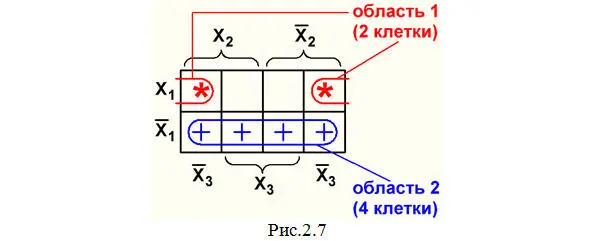
1. В карте Вейча с 8 клетками (рис.2.7).

2. В карте Вейча с 16 клетками (рис.2.8).

В каждой такой области объединения выполняется операция «склеивания», в результате которой остается только один многочлен только с теми переменными, которые входят во все объединенные клетки. А переменные типа X 1и X 1′, X 2и X 2′, X 3и X 3′, X 4и X 4′«сокращаются». Это можно объяснить на следующем примере: возьмем два многочлена СДНФ (аналогичный результат получается и с многочленами СКНФ), соответствующих двум клеткам области 1 рис.2.7:

Х 1·Х 2·X 3′ \/ X 1·X 2′·X 3′;

одинаковые переменные вынесем за скобки:

X 1·X 3· (X 2\/ X 2′);

легко проверить, что выражение в скобках при любых значениях X 2( 0 или 1) дает 1, тогда: