М. Нсанов - Цифровые устройства. Учебник для колледжей

X 1·X 3·1 = X 1·X 3.

Итак, в результате «склеивания» двух клеток области 1 рис.2.7 получается: X 1·X 3.

Приведем примеры (рис.2.10) «склеивания» клеток в карте Вейча на рис.2.4:

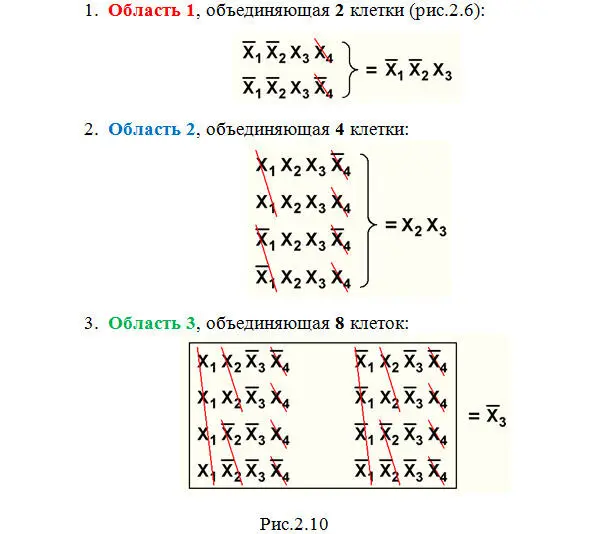
Очевидно, что при объединении всех клеток любой карты сокращаются все переменные, и результат «склеивания» дает 1.

Из сравнения полученных результатов можно сделать вывод : чем больше объединяется клеток, тем проще получается результат «склеивания» , т.е. итоговое логическое выражение содержит меньше операций, и, соответственно, схема ЦУ будет иметь меньше логических элементов.

Теперь приведем порядок минимизации :

– Чертим карту Вейча с нужным количеством клеток.

– Клетки карты, соответствующие минтермам СДНФ (или СКНФ) обозначаем символом « 1».

– Объединяем все клетки с « 1». Количество клеток в каждом объединении должно быть максимальным, а самих областей объединения должно быть как можно меньше. П р и м е ч а н и е: любое количество клеток с « 1» могут одновременно входить в две или больше области объединения.

– В каждой области производим операцию «склеивания», в результате чего получаем многочлены минимальной формы: МДНФ или МКНФ.

Приведем несколько примеров минимизации:

Пример 1. Минимизация СДНФ функции Y 1из темы 2.1 (рис.2.11):

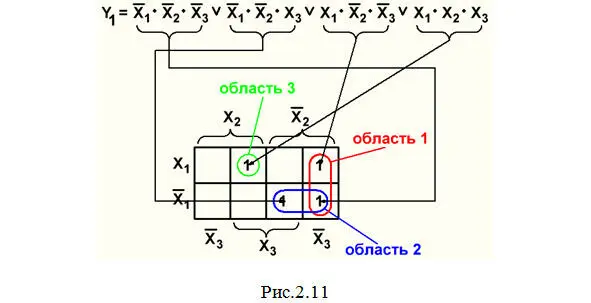
Покажем на рис.2.12 результаты"склеивания» двух клеток в областях 1 и 2 этой карты.

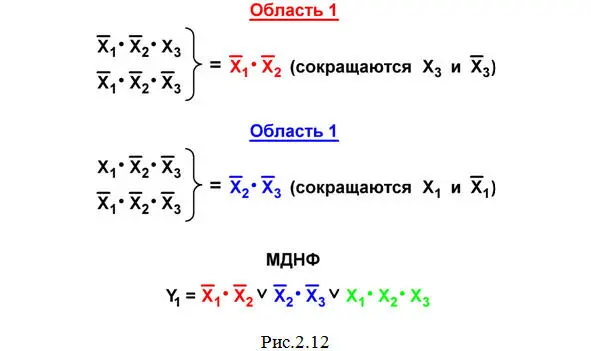
Область 3 : Эта клетка остается одна – ни с какими другими клетками, содержащими « 1», ее объединить нельзя. Поэтому соответствующий данной клетке многочлен Х 1·Х 2·Х 3не сокращается и входит в минимальную дизъюнктивную нормальную форму (МДНФ) без изменения.

В результате на этом же рис.2.12 записываем МДНФ ( красным, синими зеленымцветом показаны минтермы, которые получились в результате «склеивания» клеток в областях объединения соответствующего цвета на рис.2.11).

Пример 2 . Минимизация СДНФ функции Y 2из темы 2.1 (рис.2.13):

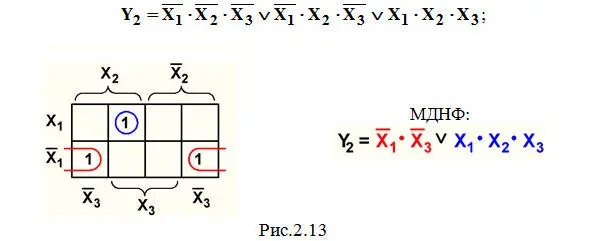
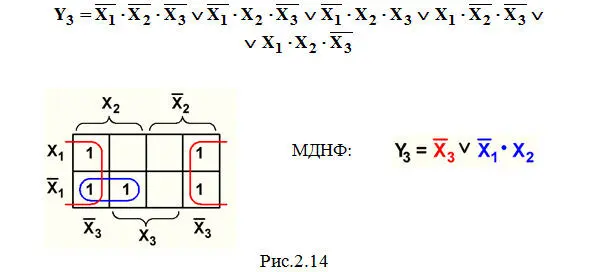
Пример 3 . Минимизация СДНФ функции Y 3из темы 2.1 (рис.2.14):

Совершенно аналогично выполняется минимизация логических функций, записанных в СКНФ. Рассмотрим примеры:

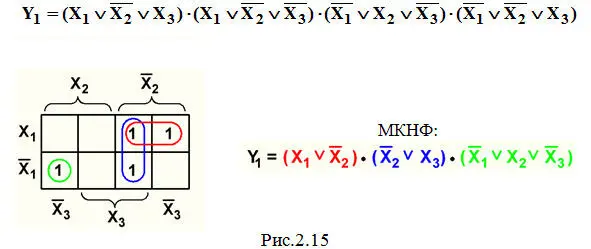
Пример 4. Минимизация СКНФ функции Y 1из темы 2.1 (рис.2.15):

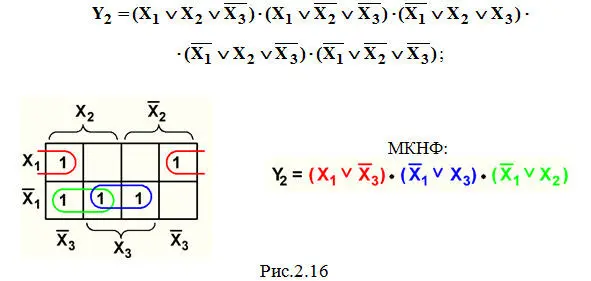
Пример 5. Минимизация СКНФ функции Y 2из темы 2.1 (рис.2.16).

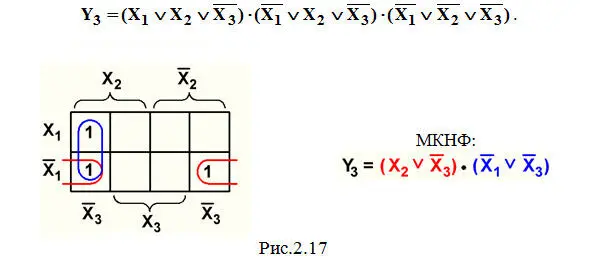
Пример 6. Минимизация СКНФ функции Y 3из темы 2.1 (рис.2.17).

***

Модификация карт Вейча, предложенная Карно, заключается в небольшом изменении координатной сетки (на рис. 2.18 показаны карты Карно для минимизации функций трех и четырех переменных дизъюнктивной формы).

Основным достоинством карт Карно по сравнению с картами Вейча является возможность их заполнения непосредственно по значениям сигналов в таблице истинности, не записывая СДНФ (или СКНФ). Но если координатная сетка карт Вейча одинаково применима для минимизации функций как дизъюнктивной, так и конъюнктивной форм, то в координатной сетке карт Карно для минимизации функций конъюнктивной формы прямые и инверсные значения переменных меняются местами по сравнению с координатной сеткой карт Карно для минимизации функций дизъюнктивной формы. На рис. 2.18 показано заполнение карт Карно, объединение клеток и результат минимизации функций Y 1(см. табл. 2.1) и Y 4в виде МДНФ.

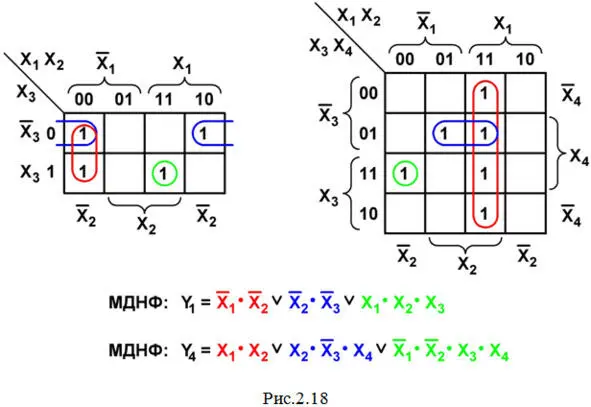
Сравнивая эти результаты с МДНФ примера 1 данной темы и примера из темы 2.8, мы легко убеждаемся, что они полностью совпадают с полученными при использовании карт Вейча.

Построение схем производится таким образом, чтобы соблюдался порядок выполнения операций в логическом выражении согласно элементарным правилам как обычной алгебры, так и алгебры логики.

Достаточно очевидно, что при построении схем ЦУ по МДНФ порядок выполнения операций должен быть следующим:

– Логическое отрицание входных сигналов Х, то есть первыми в схеме должны стоять элементы НЕ.

– Логическое умножение (элементы И).

– Логическое сложение (элементы ИЛИ).

Пример 1. МДНФ (см. пример 1 из темы 2.2):

Y1 = X 1′·X 2′ \/ X 2′·X 3′ \/ X 1·X 2·X 3.

Определяем количество операций (и, соответственно, требуемых логических элементов) для реализации этой МДНФ:

1. В данном логическом выражении стоят 4 знака операции логического отрицания. Но следует учесть, что инвертирование одного и того же сигнала X 2просто встречается два раза. Поэтому схема должна содержать 3 элемента НЕ для отрицания сигналов X 1, X 2и X 3.

2. Для выполнения первого умножения X 1′·X 2′потребуется один элемент 2И, т.к. в этой операции участвуют два сигнала: X 1′и X 2′.

3. Для выполнения второго умножения X 2′·X 3′также потребуется один элемент 2И.

4. В третьем многочлене X 1·X 2·X 3требуется умножение трех сигналов, поэтому здесь нужно использовать один элемент 3И.

Таким образом, для выполнения операций умножения мы должны использовать 2 элемента 2Ии один элемент 3И.