М. Нсанов - Цифровые устройства. Учебник для колледжей

5. Логическое сложение трех многочленов X 1′·X 2′; X 2′·X 3′и X 1·X 2·X 3требует применения одного элемента 3ИЛИ. Но нужно сразу учесть, что в серии КР1533 и во многих других нет микросхем, содержащих элементы 3ИЛИ. Поэтому для реализации нужного нам сложения придется использовать 2 элемента 2ИЛИ.

По записи МДНФ видно, что именно в такой последовательности нужно выполнять операции: сначала логическое отрицание НЕ, затем логическое умножение И, и в конце логическое сложение ИЛИ.

Подбираем микросхемы. В данном случае для построения схемы достаточно взять:

– Одну микросхему КР1533ЛН1 (см. рис.1.12), содержащую 6 элементов НЕ. Т. к. нам требуется только 3 элемента НЕ, то в данной микросхеме 3 элемента оказываются лишними и использоваться они не будут.

– Одну микросхему КР1533ЛИ1 (см. рис.1.12), содержащую 4 элемента 2И(здесь два элемента оказываются лишними), и одну микросхему КР1533ЛИ3 (см. рис.1.12), содержащую 3 элемента 3И(из нее 2 элемента использоваться не будут).

– Одну микросхему КР1533ЛЛ1 (см. рис.1.13), содержащую 4 элемента 2ИЛИ(два элемента этой микросхемы оказываются лишними).

Строим схему ЦУ в базисе И, ИЛИ, НЕ (термин « базис И, ИЛИ, НЕ» означает, что в данной схеме будут использоваться только элементы И, ИЛИ, НЕ), причем операции должны производиться в установленной нами последовательности: сначала НЕ, затем И, и в конце ИЛИ. Обращаем внимание, что при необходимости указывать направление передачи сигналов входы и выходы могут быть начерчены не кружочками (как в Разделе 1), а стрелками.

а) Чертим все три входа Х 1, Х 2и Х 3(рис.2.19а).

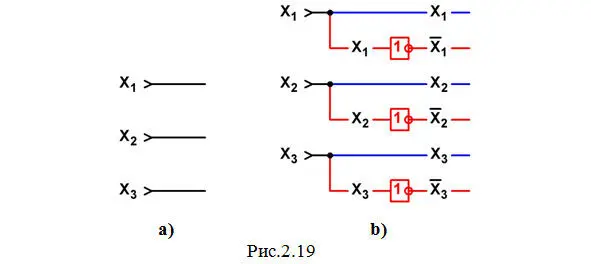
В дальнейшем на каждом следующем этапе все новые элементы, которые будут включаться в схему, показываются краснымцветом.

b) Смотрим на МДНФ и видим, что операции НЕ должны выполняться в данном случае со всеми тремя переменными, т.к. в этом выражении имеются величины X 1′, X 2′и X 3′. Поэтому на всех трех входах ставим элементы НЕ (рис.2.19b.). Входы элементов подключаем ко входам схемы X 1, X 2и X 3, на выходах будут формироваться инверсные значения входных сигналов X 1′, X 2′и X 3′.

Сразу же нужно учесть еще один момент: снова смотрим на МДНФ и обнаруживаем, что наряду с инверсными значениями всех (еще раз повторяем: в данном случае всех) сигналов X 1′, X 2′и X 3′нам потребуются и их прямые значения, поэтому выводим в схему и провода, показанные синимцветом.

c) Теперь переходим к выполнению операций логического умножения. Начнем с операции X 1′·X 2′(смотрите МДНФ). Чертим элемент 2И; на один его вход подаем X 1′, на другой – X 2′; на выходе получаем результат умножения: X 1′·X 2′. К настоящему моменту мы будем иметь схему, изображенную на рис.2.20a.

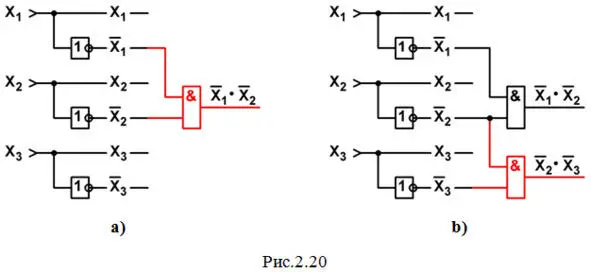
d) Реализуем следующую операцию умножения: X 2′·X 3′(смотрите МДНФ). Чертим еще один элемент 2И; на один его вход подаем X 2′, на другой – X 3′; на выходе получаем результат: X 2′·X 3′. Теперь схема примет вид рис.2.20b.

e) В последнем многочлене МДНФ X 1·X 2·X 3нужно выполнить операцию умножения с тремя сигналами, поэтому чертим элемент 3И. На один его вход подаем X 1, на второй – X 2и на третий – X 3; на выходе получим результат: X 1·X 2·X 3. И схема теперь будет иметь вид рис.2.21.

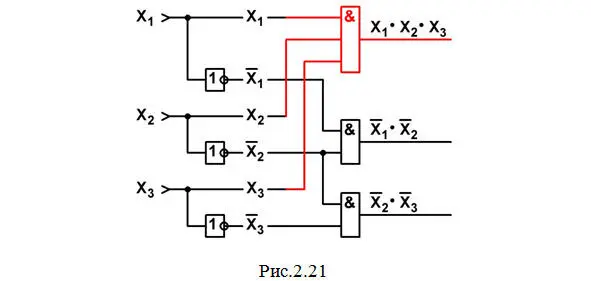
f) Переходим к реализации операций логического сложения полученных многочленов: X 1′·X 2′, X 2′·X 3′и X 1·X 2·X 3с помощью двух элементов 2ИЛИ. Как известно, при перемене мест слагаемых сумма не меняется; поэтому совершенно безразлично, в какой последовательности мы будем выполнять эти операции. Начнем с логического сложения многочленов X 1′·X 2′и X 1·X 2·X 3. Начертим элемент 2ИЛИ; на один его вход подадим X 1′·X 2′, на другой – X 1·X 2·X 3; на выходе получим результат сложения: X 1′·X 2′\/ X 1·X 2·X 3. Теперь схема будет выглядеть так, как на рис.2.22.

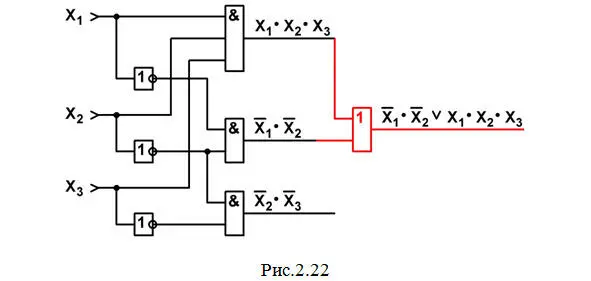
g) Остается лишь к величине ( X 1′·X 2′\/ X 1·X 2·X 3) прибавить многочлен X 2′·X 3′. Чертим последний элемент – элемент 2ИЛИ; на один его вход подаем ( X 1′·X 2′\/ X 1·X 2·X 3), на другой – X 2′·X 3′; на выходе этого элемента (так как он последний) получаем значение выходной функции Y 1. И схема примет вид рис.2.23.

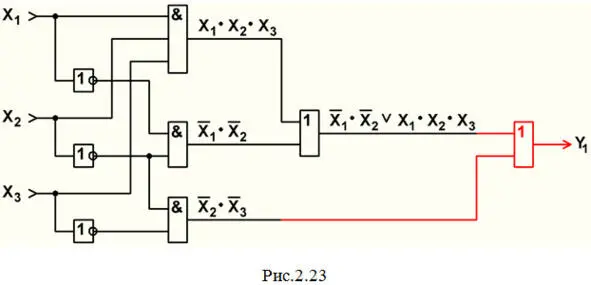
Теперь уберем вспомогательные надписи, укажем входы и выход, проставим позиционное обозначение всех элементов схемы с соответствующей нумерацией.

Микросхемы на чертежах обозначаются буквой D(от английского d evice – устройство) с соответствующим номером, например: D1, D2, D3и т. д. Допускается в позиционное обозначение добавлять вторую букву: DА(A – a nalogy ) – аналоговая микросхема, DD(D – d igital ) – цифровая микросхема; но это делается обычно тогда, когда в схеме присутствуют микросхемы обоих типов. А так как у нас в дальнейшем на чертежах будут только цифровые микросхемы, то мы вторую букву ставить не будем. Нумерацию микросхем и любых других элементов следует по возможности выполнять сверху вниз «колонками», начиная с левой стороны схемы.

На нашем чертеже в первой колонке стоят элементы НЕ из микросхемы КР1533ЛН1, которую поэтому следует обозначить D1. Но как обозначить отдельные элементы этой ИМС? Существует следующее правило: если микросхема содержит несколько элементов, то они обозначаются с двойной нумерацией через точку , причем первая цифра указывает номер микросхемы, а вторая – номер элемента в этой микросхеме. В данном случае первый элемент НЕ из микросхемы КР1533ЛН1 (напомним, что ее мы обозначили D1) нужно обозначить D1.1, второй элемент – D1.2, третий – D1.3.