Микаэль Лонэ - Теорема зонтика, или Искусство правильно смотреть на мир через призму математики

Но отмеченные вами цифры вызывают смутное сомнение. Вам не кажется, что в этой череде что-то не так? Некий дисбаланс. Она преимущественно состоит из 1 и 2, перемежаясь то тут, то там 3, 4, 5, 6, 7, 8 и 9. Как будто мы, сами того не осознавая, обращали наше внимание на самые низкие цены. Так не пойдет.

Так что давайте поступим как добросовестные статистики. Оставим в стороне наши предубеждения и выберем систематический метод. Мы случайным образом укажем на несколько полок и выпишем значимые цифры со всех товаров без исключения. Да, это трудоемкая задача, но мы должны разобраться с ней до конца.

Через час страницы вашего блокнота покрыты рядами цифр. Пришло время подвести итоги. После подсчета вердикт не подлежит обжалованию, и тенденция подтвердилась. Вы перечислили цены на более чем тысячу товаров, и почти треть из них начинается с 1! Чуть больше четверти начинается с 2, и чем больше цифра, тем реже она встречается.

После компиляции мы пришли к следующим результатам [1] Эти данные собраны автором в январе 2019 года, согласно описанному выше методу, на основе учета 1226 товаров. Результаты таковы: цифра 1 – 391 товар (31,9 %), цифра 2 – 315 (25,7 %), цифра 3 – 182 (14,8 %), цифра 4 – 108 (8,8 %), цифра 5 – 66 (5,4 %), цифра 6 – 50 (4,1 %), цифра 7 – 40 (3,3 %), цифра 8 – 30 (2,4 %), цифра 9 – 44 (3,6 %). — Здесь и далее примечания автора, если не указано иное. .

В этот раз мы не можем сослаться на случайность или предвзятый выбор товаров. У нас есть доказательства, а потому надо признать факт: первые цифры цен в супермаркете распределены неравномерно. Преобладают – со значительным отрывом – небольшие цифры.

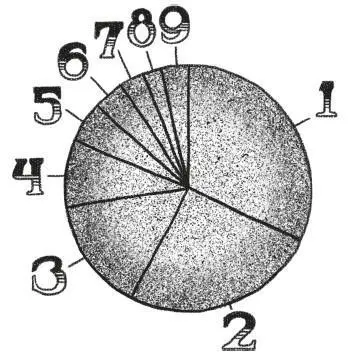
Откуда этот дисбаланс? Вот вопрос, который я хотел бы вам задать. Какому закону супермаркетов, торговли или экономики подчиняются эти ценники, чтобы дать такое странное, такое неравномерное распределение первых цифр? Разве математика не должна относиться ко всем цифрам [2] Формально формулировка «значение цифры» математически безграмотна: значение есть у числа, у цифры – нет. Цифра – способ записи числа. – Прим. ред. одинаково – без предвзятости, без предпочтений, без фаворитов? И все же факты налицо и категорически утверждают обратное: в супермаркете у математики есть любимчики – цифры 1 и 2.

Мы провели наблюдение. Мы установили закономерность. Теперь нам остается только подумать над ней, проанализировать и разобраться. У нас есть факты, и мы должны провести расследование и сделать свои выводы.

В марте 1938 года американский инженер и физик Фрэнк Бенфорд опубликовал статью «Закон аномальных чисел» (The Law of Anomalous Numbers), в которой он проанализировал числовые данные, полученные из более чем двадцати тысяч источников различного происхождения. В его таблицах можно найти список длин рек из разных частей земного шара, население разных городов США, атомные массы известных элементов, числа, случайно наблюдаемые в газетах, или математические константы. И по всем этим данным Бенфорд делает тот же вывод, что и мы: первые цифры распределены неравномерно. Около 30 % проанализированных чисел начинаются с 1, 18 % – с 2, и чем больше цифра, тем реже она встречается; так, только 5 % чисел начинаются с 9.

Бенфорду не пришла в голову идея проверить свою статистику в магазине. Но согласитесь: его результаты удивительно похожи на наши. Конечно, есть некоторые различия в процентах, но в общих чертах совпадение поразительно.

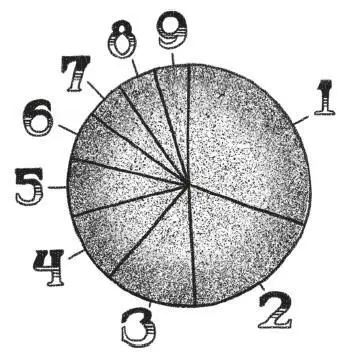
Исследование Бенфорда показало, что собранные нами данные – далеко не единичный пример. Они характерны не только для супермаркетов, но вписываются в гораздо более широкую тенденцию. После 1938 года такое же распределение наблюдалось многими учеными во множестве необычных и разнообразных ситуаций.

Например, в демографии. Население 62 из 203 стран на планете Земля – или 30,5 % – записывается числом, которое начинается с цифры 1. Взять, к примеру, самую густонаселенную: Китай с населением 1,4 млрд человек. К этим 62 странам также относится Мексика с населением 122 млн человек, Сенегал с населением 13 млн или архипелаг Тувалу с населением 10 800. При этом лишь в 14 странах (6,9 %) запись числа населения начинается с цифры 9.

Вам предпочтительнее астрономия? Из восьми планет, вращающихся вокруг Солнца, у четырех запись длины экваториального диаметра [3] Планеты Солнечной системы сплюснуты у полюсов, поэтому полярный диаметр у них меньше экваториального. – Прим. ред. начинается с цифры 1. У Юпитера – 142 984 км, у Сатурна – 120 536, у Земли – 12 756, у Венеры – 12 104. Диаметр самого Солнца составляет 1 392 000 км. И если выборка из девяти небесных тел недостаточно полна, чтобы вас убедить, добавьте сюда же карликовые планеты, спутники, астероиды, а также кометы, и вы все равно придете к тому же выводу: превалирует цифра 1.

Как только мы начинаем обращать на это внимание, примеры сыплются дождем. Возьмите любой набор чисел в любом контексте, проанализируйте первые цифры, и увидите: закон Бенфорда работает. Этот статистический закон совсем не исключительный, он, похоже, совершенно естественный и повсеместный. И, как ни парадоксально, равномерного [4] В статистике его также называют «справедливым». — Прим. ред. распределения цифр, которое могло бы показаться нам более интуитивно-вероятным, на практике просто не существует.

Здесь речь идет уже не о любопытном свойстве цен в супермаркетах. То, что мы обнаружили, – это настоящий закон, который регулирует не только многие области человеческой деятельности, но и саму природу. Понять этот закон – значит понять нечто фундаментальное об устройстве нашего мира.

Его влияние настолько велико, что мы подчиняемся ему, даже не осознавая этого. Люди, которые устанавливают цены в магазинах, не договариваются друг с другом и едва ли слышали о Фрэнке Бенфорде. И все же, неосознанно, словно ими манипулирует неподвластная им сила, они подчиняются его закону. Как и население стран, длины рек и диаметры планет.

В 1938 году Фрэнк Бенфорд назвал это распределение «законом аномальных чисел». Тем не менее этот закон настолько распространен, что такое название кажется неуместным. Аномальность субъективна и существует только в умах людей, которые ей поражаются. Природа, напротив, кажется, находит этот закон универсальным. Закон аномален только до тех пор, пока мы его не поймем. И мы намерены его понять.

Но в каком направлении двигаться? Как направить наши мысли, чтобы приоткрыть завесу тайны и понять аномалии? [5] «Аномальными» Бенфорд назвал эти числа потому, что обнаруженные им корреляции не были идеально строгими – некоторые наборы данных на тот момент описывались этим законом лучше, некоторые – хуже. Сам Бенфорд считал, что его закон имеет ограниченное применение – только к тем числам, между которыми не имеется связующих закономерностей. Впоследствии этот закон начали называть просто «законом Бенфорда». – Прим. ред.