Владимир Живетин - Методы и средства обеспечения безопасности полета

В данной главе мы будем формировать математическую модель количественной оценки функционирования системы. С этой целью разработаем математическую модель движения финансовых потоков через микроэкономическую систему.

На основе вышеизложенного сформируем требования к математической модели финансовых потоков, порожденных микроэкономической системой. Модель должна:

– содержать средства анализа поведения финансовых потоков при введении различных управляющих воздействий;

– позволять прогнозировать прибыль в различные моменты времени;

– отражать влияние внешних и внутренних возмущающих факторов, обусловливающих потери микроэкономической системы.

При оценке потерь и прибыли будем рассматривать финансовые потоки, порожденные пассажиропотоком или грузопотоком в единицу времени данным самолетом в рамках системы.

Для вывода уравнения, описывающего финансовые потоки, формируемые в процессе эксплуатации самолета как финансовой системы, воспользуемся балансом потоков финансовых средств, поступающих на вход и затрачиваемых системой в некоторый момент времени t. Примем, что процесс поступления средств и расходы на реализацию полетов для перевозки пассажиров или (и) грузов происходят непрерывно во времени. Это приемлемо, так как мы предполагаем, что данный самолет в единицу времени перевозит достаточно большое количество пассажиров или грузов, а рассматриваемый интервал времени достаточно большой. Например, если единица времени – сутки, за которые самолет совершил несколько полетов, а общий интервал времени – десятки суток, то данное допущение приемлемо. Отметим, что данное допущение не принципиально. При необходимости в дальнейшем мы всегда можем перейти к дискретной модели, описывающей процесс от одного полета до другого.

В дальнейшем будем пользоваться средними значениями величин на малом, но конечном интервале времени. В рассматриваемых условиях это финансовые или энергетические потоки. Эти величины будем считать непрерывными и дифференцируемыми по времени без специальных оговорок.

Составим уравнение баланса финансовых потоков на входе и выходе объекта (рис. 1.13) в произвольный момент времени t. Термин «поток» в дальнейшем понимается как изменение изучаемой величины (процесса) в единицу времени, т. е. как производная рассматриваемой величины по времени.

При этом имеет место следующая модель баланса финансовых потоков [16, 19]:

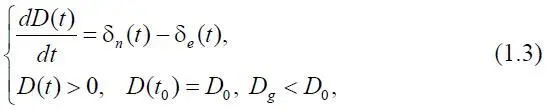
где D = D ( t ) – объем финансовых средств микроэкономической системы, созданных ею на данный момент времени t в процессе своего функционирования; δ n = δ n ( t ) – поток поступающих финансовых средств; δ e = δ e ( t ) – поток расходов, т. е. средств, направленных на реализацию процесса «пассажиропотока» («грузопотока»); D g – гарантированный запас средств в микроэкономической системе, ниже которого объем средств опускаться не должен, поскольку в этом случае микроэкономическая система не сможет функционировать; D 0 – объем имеющихся средств, включая стоимость самолета (величина непостоянная для каждого самолета) и средств реализации полетов, в начальный момент времени t = t 0, которые можно назвать депозитом (как в банке).

Завершение этапа функционирования (при t = T ) самолета происходит либо по причине выработки ресурса, либо по причине катастрофы, либо на конкурентной основе. При этом имеем время работы самолета, т. е. время Т получения прибыли.

Система (1.3) описывает баланс финансовых динамических потоков, который представляет одну из форм проявления фундаментальных законов сохранения энергии в технико-экономической среде.

Поток расходов δ e ( t ) представим в виде

δ e ( t ) = δ k ( t ) + δ g ( t ) + δ r ( t ), (1.4)

где δ k ( t ) – поток средств, направляемых на организацию максимальных пассажироперевозок на рынке услуг; δ g ( t ) – поток средств, направленный на компенсацию средств, полученных по договору лизинга; δ r ( t ) – поток средств на организационно-техническое обслуживание микроавиационной системы (самолет и система обслуживания), включая ремонт и восстановление техники после аварий и катастроф.

При этом, как правило, внедрение новой техники увеличивает расходы, т. е. δ k ( t ), но уменьшает вероятность Р 2аварий и катастроф, т. е. материальных затрат.

Представим поток δ r в виде

δ r ( t ) = δ s ( t ) + δ ca ( t ) + δ T ( t ) + δ o ( t ), (1.5)

где δ зп ( t ) – поток заработной платы; δ oc ( t ) – поток расходов на развитие основных средств; δ н ( t ) – поток налогов; δ пр ( t ) – поток средств на прочие расходы.

Поток поступлений имеет место с рынка услуг. Эти поступления включают

δ n ( t ) = δ p ( t – τ)[1 + П *( t – τ)], (1.6)

где δ p ( t ) – финансовые потоки, формируемые системой, согласно стоимости услуг в момент времени ( t – τ), т. е. предшествующий моменту времени их оказания t; П* (·) – компенсационная компонента на оказываемые услуги, назначенная в процессе анализа и прогнозирования рынка услуг и состояния среды функционирования микроэкономической системы.

Величину П* (·) представим в виде

где τ – время в днях, в течение которого осуществляется подготовка и реализация услуг пассажироперевозок; П ( t – τ) – проценты на вложение δ p назначенные в момент времени ( t – τ). Проценты П * ( · ) назначает микроавиационная система – на вложение, т. е. то, что должен возвратить ей потребитель услуг, например, пассажир.

Поясним роль и место τ в соотношении (1.6), которое записано для момента времени t возврата вложенных средств. Считаем, что «кредит» выдан в момент времени t* = t – τ (рис. 1.14). Мы предполагаем, что финансы могут выдаваться непрерывно во времени и на время τ = const (рис. 1.15).

Кроме того, возможны ситуации когда δ p могут выдаваться на различное время τ i в различные моменты времени t i . При этом модель δ n должна быть дискретной, т. е. рассматриваться δ n ( t i ), а соотношение (1.6) должно быть записано в виде

δ n ( t i ) = δ p ( t i – τ i )[1 + ξ( t i – τ i )].

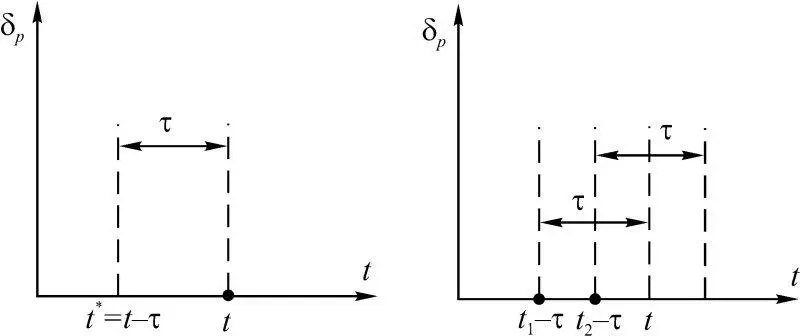
Рис. 1.14 Рис. 1.15