Владимир Живетин - Методы и средства обеспечения безопасности полета

Подставив (1.11) в (1.10), заменяя s на t в силу произвольности s , получим

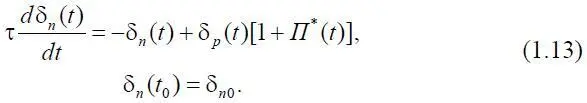
В общем случае нелинейная зависимость δ n ( s +τ) заменена линейной δ n ( s ), а чистое запаздывание τ, свойственное системе, заменено на инерционное τ k , свойственное динамической системе. Однако инерционное и чистое запаздывания не равны. При этом имеет место приближенное равенство

τ = 3τ k ,

которое следует из условия вхождения решения уравнения (1.13) в 5 %-ю полосу, т. е. совпадения.

В (1.13) выразим δ p через δ e , что позволит свести исходную систему к системе из двух уравнений с двумя неизвестными, т. е. замкнутую систему.

Поток δ r ( t ), согласно (1.5), состоит из ряда слагаемых, которые представим в следующей форме:

δ зп = γ 1δ e ; δ н = γ 2δ e ; δ ос = γ 3δ e ; δ пр = γ 4δ e ,

где γ 1, γ 2, γ 3, γ 4определяют доли, которые составляют от δ e потоки δ s , δ Т , δ са , δ o соответственно.

Следовательно δ r ( t ) = γδ e , где γ = γ 1+ γ 2+ γ 3+ γ 4. При этом часть δ e , равная δ p = (1 – γ)δ e , идет на компенсацию депозита, т. е. δ g ( t ) и создание услуг, которые еще не оплачены, т. е. в некотором смысле на кредит, выдаваемый пассажирам под проценты П *.

При этом неравенство δ p > 0 будет характеризовать функционально-экономическую устойчивость системы, поскольку величина δ р характеризует объем средств, вкладываемых в организацию и проведение пассажироперевозок. Из соотношения δ p = (1 – γ)δ e > 0 следует неравенство δ e > 0, что также характеризует функционально-экономическую устойчивость.

С учетом принятых допущений и полученных уравнений (1.9), (1.13) система примет вид

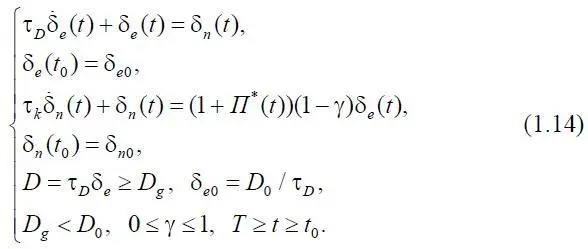
Эта система является замкнутой относительно δ e ( t ) и δ n ( t ). Одним из управлений служит параметр γ, определяющий долю затрат всех средств, кроме тех, что идут на организацию пассажироперевозок (грузоперевозок). Кроме того, П *( t ) включен в управление системой, ее технико-экономическим потенциалом.

Система содержит два параметра τ D и τ k , характеризующие динамические свойства системы, и их следует идентифицировать. После этого система (1.14) будет описывать финансовые потоки изучаемой системы.

Сначала проанализируем статически равновесное состояние системы, когда δ n и δ e – постоянные величины. При этом 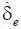= = 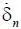0. Тогда из (1.3) следует, что δ e = δ n , т. е. расход всегда равняется поступлениям, и это будет иметь место, если

(1 – γ)(1+ П *) = 1, (1.15)

или доля расходов γ удовлетворяет условию

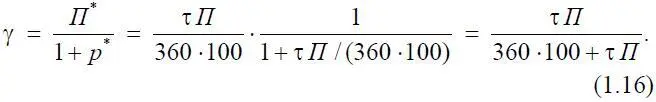
Обобщенным параметром, определяющим допустимые расходы, выступает произведение τ П . На рис. 1.17 представлен график зависимости (1.16).

Теперь, исключив величину δ n из системы (1.14), получим одно дифференциальное уравнение второго порядка относительно δ e ( t ):

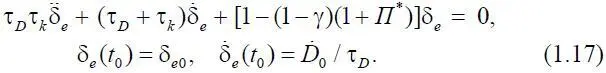
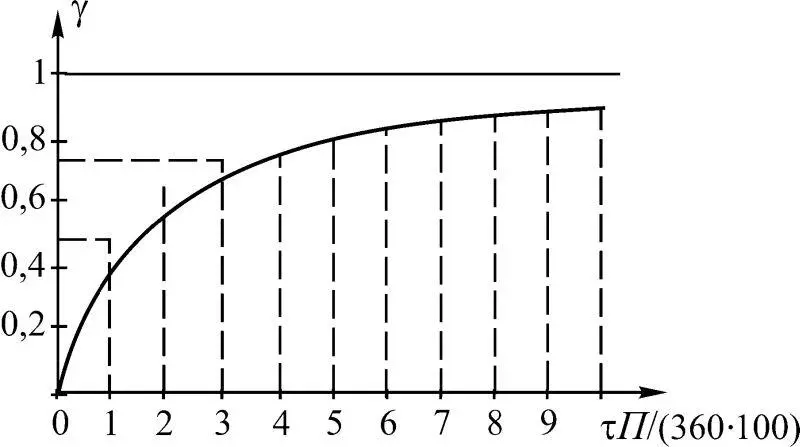
Рис. 1.17

После определения величины δ e из уравнения (1.17) неизвестная величина δ n может быть определена из первого уравнения (1.14). Если решение (1.17) получено численно, то для вычисления δ n необходимо использовать третье уравнение из (1.14), поскольку численное дифференцирование δ e приводит к появлению существенных погрешностей.

Если коэффициенты уравнения (1.17) постоянны, то несложно получить его аналитическое решение. Для этого запишем характеристическое уравнение

τ D τ k λ 2+ (τ D + τ k ) λ + [1 – (1 – γ)(1 + П *)] = 0, (1.18)

решения которого

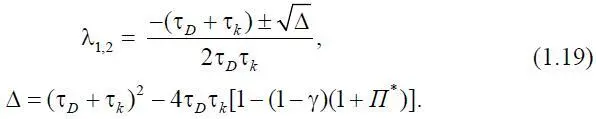
Если равенство (1.15) не выполняется, то в зависимости от величины и знака дискриминанта Δ корни λ 1,2будут вещественными или комплексными. Введем следующие обозначения:

a = τ D + τ k ; b = 4τ D τ k [1 – (1 – γ)(1 + П *)].

Тогда А = a 2– b.

Величина a , как правило, положительна. Она будет отрицательна, если одна из величин – τ D или τ k – отрицательна, и при этом τ D + τ k < 0. Это означает, что рассматривается процесс не с запаздывающим, а с опережающим аргументом. Например, выданные в кредит деньги возвращаются не после, а до выдачи кредита. Эти и аналогичные им случаи здесь не рассматриваются. Примем, что a > 0 всегда.

Величина b может быть как положительной, так и отрицательной. В зависимости от соотношения величин a 2и b дискриминант Δ может иметь разный знак.

Рассмотрим следующие случаи.

При a 2> b дискриминант Δ > 0, и оба корня уравнения (1.18) вещественны. В этом случае общее решение уравнения (1.17) имеет вид

δ e = exp(– at )[(( c 1+ c 2)/2)exp( ct ) + (( c 1 c 2)/2)exp(– ct )], (1.20)

где c = 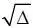= 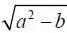. Постоянные c 1и c 2зависят от начальных данных δ e 0и 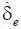и параметров системы следующим образом:

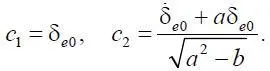
Случай b = 0 соответствует равновесному состоянию рассматриваемой системы, при этом выполняется условие (1.15), Δ = a 2и λ 12= – a ± a , то есть λ 1= 0, λ 2= –2 a. Тогда общее решение (1.20) запишется в виде

δ e = ( c 1+ c 2) / 2+(( c 1– c 2) / 2) exp (–2 at ).

Равновесное состояние δ e = ( c 1+ c 2) / 2 реализуется при любом значении t , если имеет место равенство c 1= c 2. Если же c 1≠ c 2, то в силу того, что a > 0, данное состояние реализуется для больших значений t , при этом

δ e ≈ ( c 1+ c 2) / 2, (1.21)

а при t , стремящемся к бесконечности, условие δ e =( c 1+ c 2) / 2 соблюдается независимо от значений c 1и c 2. Таким образом, состояние δ e =( c 1+ c 2) / 2 обладает устойчивостью финансового потока по отношению к начальным возмущениям (рис. 1.18).