Владимир Живетин - Методы и средства обеспечения безопасности полета
- Название:Методы и средства обеспечения безопасности полета
- Автор:
- Жанр:
- Издательство:Изд-во Института проблем риска, Информационно-издательский центр «Бон Анца»
- Год:2010
- Город:Москва
- ISBN:978-5-98664-055-6, 978-5-903140-39-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Живетин - Методы и средства обеспечения безопасности полета краткое содержание
Методы и средства обеспечения безопасности полета - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Рассмотрим введенные выше коэффициенты γ 2, γ 3, γ 4и γ 5, характеризующие части дохода A δ k ( t – τ), направленные на формирование финансовых потоков δ зп ( t ), δ н ( t ), δ ос ( t ) и δ пр ( t ) соответственно, где δ зп ( t ) – поток заработной платы; δ н ( t ) – поток налогов; δ ос ( t ) – поток расходов на развитие основных средств; δ пр ( t ) – поток средств на прочие расходы.
При этом получим
δ k ( t )=δ k ( t – τ)+γ 1 A δ k ( t – τ); δ зп ( t )=γ 2 A δ k ( t – τ);
δ н ( t )=γ 3 A δ k ( t – τ); (1.24)
δ ос ( t )=γ 4 A δ k ( t – τ); δ пр ( t )=γ 5 A δ k ( t – τ).
Обозначим через γ=γ 1+γ 2+γ 3+γ 4+γ 5. Если вся прибыль направляется в оборот, то γ=1, условие γ < 1 означает, что часть средств отправлена на накопление. В этом случае расходная часть δ e в (1.23) должна включать в себя дополнительную компоненту δ накопл = A δ k ( t – τ).
Соотношения (1.24) записаны для идеальной ситуации, когда поступившие деньги передаются внешним потребителям без запаздывания. В действительности микроавиационная система, как и любой другой реально функционирующий механизм, исполняет действия с запаздыванием (например, это время, необходимое для обработки документации). Обозначим его через τ 0. В общем случае τ 0имеет различные значения при передаче различных составляющих δ e различными службами и отделами микроавиационной системы.
Рассмотрим частный случай, когда величина τ 0неизменна для всех подсистем. При этом соотношения (1.24) примут форму
δ k ( t )=(1+γ 1 A )δ k ( t – τ 1); δ зп ( t )=γ 2 A δ k ( t – τ 1); δ н ( t )=γ 3 A δ k ( t – τ 1);
δ ос ( t )=γ 4 A δ k ( t – τ 1); δ пр ( t )=γ 5 A δ k ( t – τ 1), (1.25)
где τ 1=τ+τ 0. Если при этом выполняется условие γ=1, то неконтролируемых расходов нет. Тогда с учетом полученных зависимостей равенства (1.4) и (1.6) примут вид
δ e ( t )=γ *A δ k ( t – τ,); δ n ( t )=(1+ A )δ k ( t – τ,), (1.26)
где γ*=γ 1+(1+γ 2)+γ 3+γ 4+γ 5в общем случае не равно двум.
Преобразуем первое уравнение в (1.26). Для этого введем замену s = t – τ 1и разложим δ e ( s +τ 1) в ряд Тейлора. Ограничившись первым членом разложения в силу малости производных более высоких порядков, получим δ e ( s +τ 1)=δ e ( s )+ 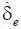 ( s )τ 1. Тогда
( s )τ 1. Тогда
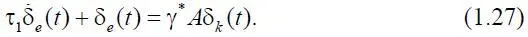
Положим, что кредит выдан на срок, больший, чем одни сутки, запаздывание τ 0по проведению финансовых операций составляет не менее одних суток в силу выбранной системы отсчета. При этом система (1.23) с учетом (1.27) примет следующий вид:
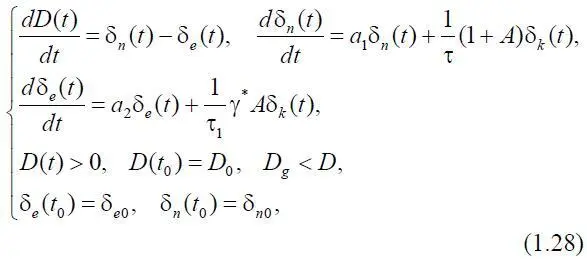
где a 1=–1 / τ, a 2=–1 / τ 1; τ ≥ 1; τ 1> 1. Система (1.28) содержит три уравнения и три неизвестных: D ( t ), δ e ( t ) и δ n ( t ), являясь, таким образом, замкнутой. В качестве управления выступает поток кредитных средств δ k ( t ). При заданных начальных условиях D ( t 0), δ e ( t 0) и δ n ( t 0) система (1.28) имеет решение (τ ≠ 0; τ 1≠ 0), если она совместна.
Для анализа полученной модели сведем рассматриваемую систему уравнений к одному уравнению третьего порядка
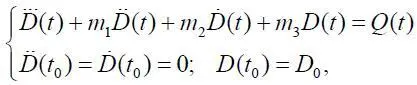
где
Q ( t )= B 1 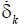 – B 2
– B 2 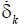 – ( B 1 a 2– B 2 a 1)δ k ; B 1=(1 / τ)(1+ A );
– ( B 1 a 2– B 2 a 1)δ k ; B 1=(1 / τ)(1+ A );
B 2=(1 / τ) 1γ *A; m 1=–( a 1+ a 2); m 2= a 1 a 2; m 3=0.
С учетом того, что m 3=0, m 1=const, m 2=const запишем это уравнение в форме
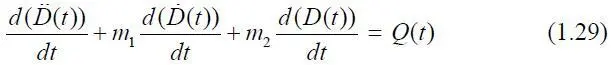
или
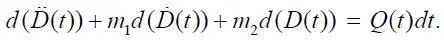
Проинтегрировав (1.29), получим
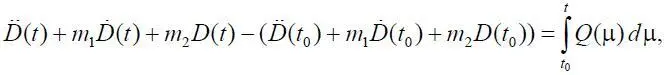
где 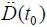 =0;
=0; 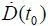 =0. Окончательно имеем
=0. Окончательно имеем
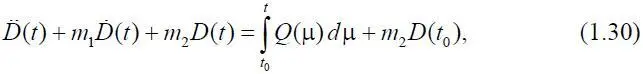
где
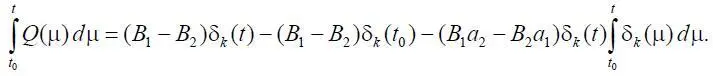
Устойчивость полной модели
Применим модель (1.30) для анализа финансового состояния микроавиационной системы. Для этого запишем ее в следующем виде:
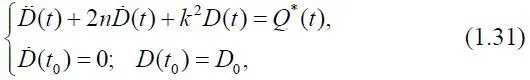
где 2 n = т 1=(τ 1+τ)/ττ 1; k 2= m 2=1/ττ 1; τ 1=τ+τ 0;
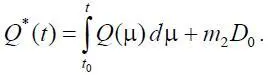
Очевидно, что модель (1.31) пригодна для использования в качестве математической модели только в том случае, если она устойчива. Покажем, что это так. Для этого проанализируем состояние микроавиационной системы без влияния внешних воздействий ( Q *( t )=0), при этом уравнение (1.31) представим в виде
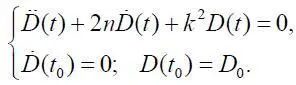
Это уравнение описывает свободные изменения оборотного капитала D ( t ) микроавиационной системы. В общем случае при малых начальных возмущениях процесс D ( t ) может быть либо сходящимся (к D ( t 0)), что будет означать устойчивость, либо расходящимся – в противном случае.
В соответствии с теорией систем [28, 29] уравнение (1.31) при Q* ( t )=0 имеет общее решение D ( t )= c 1exp(λ 1 t )+ c 2exp(λ 2 t ), где λ 1и λ 2 – корни характеристического уравнения
λ 2+2 n λ+ k 2=0.
Покажем, что эти корни действительны и различны, т. е. λ 1,2=–n ± 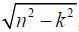 , где ( n 2– k 2) > 0.
, где ( n 2– k 2) > 0.
С учетом того, что 2 n =(2τ+τ 0)/(τ(τ+τ 0)) и k 2=1/(τ(τ+τ 0)), разность n 2– k 2={τ 3 0: [4τ(τ+τ 0)]} > 0, поскольку τ > 1, τ 0≥ 1. Кроме того, полученным значениям n и k соответствуют отрицательные собственные значения.
Сказанное говорит об устойчивости системы (1.31) в соответствии с теорией систем. Это означает, что при принятых условиях микроавиационная система устойчива. При этом оборотный капитал микроавиационной системы при δ k ( t )=0 останется неизменным, т. е. микроавиационная система, не выделяющая кредиты, не может быть убыточной или прибыльной. При отсутствии прибыли нет и всех тех расходов, которые включены в расходную часть δ e ( t ). Отметим, что в соответствии с существующим законодательством не все налоги оплачиваются, исходя от прибыли. Это, в свою очередь, означает, что модель (1.31) не совсем верна, поскольку при δ k ( t )=0 выполняется условие δ н ( t )=0. Для более тщательного анализа необходимо принять δ н ( t )=γ 3 A δ k ( t – τ)+ c 1, где c 1 – постоянная величина, определенная с учетом действующего законодательства.
Читать дальшеИнтервал:
Закладка:










