Владимир Живетин - Методы и средства обеспечения безопасности полета

Пусть безрисковая кредитная процентная ставка 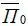составляет 200 процентов в год и складывается из инфляционной составляющей, равной 190 процентам, и безинфляционной, равной 10 процентам. При этом мы исходим из простейшей модели суммирования ставок. Тогда относительная процентная ставка 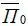равна 0,2. Допустим, что расчетное значение вероятности P* 4находится на уровне 0,2. Тогда, согласно формуле (1.39), величина относительного кредитного процента равна 2,0+0,8·(1+0,2)/(1 – 0,2)=2,75. Таким образом, в данном случае микроавиационная система вправе назначать процентную ставку П =275 %. Рассмотрение этого примера при отсутствии инфляции (инфляционная составляющая кредитного процента равна нулю) дало бы следующие значения величин: 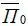=0,1; 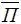=0,375; П =37,5 %.

Влияние инфляции на величину возвращаемого кредита в условиях риска невозврата проявляется через безрисковый возврат, который, как видно из формулы (1.42), непосредственно зависит от безрисковой ставки 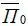, содержащей инфляционную составляющую. В зависимости от соотношения процента инфляции и процента риска тот или иной фактор способен оказывать решающее воздействие на цену кредита.

В процессе разработки показателей технико-экономического риска для самолета необходимо учитывать все четыре этапа его жизненного цикла. На первом этапе учитывается роль науки; на втором этапе – роль конструкторско-проектных работ; на третьем – роль технологических процессов производства самолета; на четвертом – проблема эксплуатации и, прежде всего, обеспечения безопасности и оптимальности полета. При этом величина технического риска есть интегральная характеристика, обусловленная потерями, для компенсации которых на самолетах устанавливают системы оптимизации режимов пилотирования (СОРП), системы предупреждения критических режимов (СПКР).

На этапе научно-исследовательских работ, cвязанных с созданием самолета, мы работаем, как правило, с математическими моделями. При этом мы имеем дело с двумя видами моделей проектируемого самолета: М 1и М 2(рис. 1.23). Модель М 1описывает функционирование реального объекта, М 2 – модель, принятая при расчетах.

Для рассматриваемой ситуации

x ( t )=Ψ( z, A, W, V, t ), y ( t )=Ψ 1( z, A , δ, t ),

где x ( t ); y ( t ) – выходные процессы для реального объекта и для математической модели соответственно; z ( t ) – входной заданный (известный) процесс, используемый для анализа; Ψ, Ψ 1 – операторы, описывающие модели М 1и М 2соответственно; δ( t ) – погрешность модели или метода, разработанного в теории; А – вектор заданных параметров, в том числе случайных возмущающих факторов; W, V – соответственно внешние и внутренние возмущающие факторы.

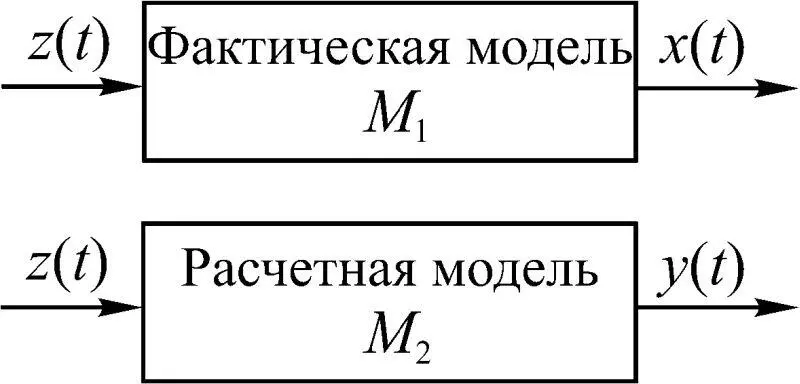
Рис. 1.23

О свойствах вектора x ( t ) на начальном этапе научно-исследовательских работ, как правило, мы имеем мало информации, но можем предположить, что в общем случае х i ( t ) ≠ y i ( t ) 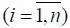. При этом x ( t ) есть фактическое значение параметров состояния объекта х ф в силу того, что в модели М 1учтены все внутренние и внешние возмущающие факторы и особенности систем, его насыщающих. При этом процессе y ( t ) получен на выходе модели М 2, которую нам дала теория (наука). Именно этой моделью мы владеем и пользуемся при проведении научно-исследовательских работ, а на выходе ее имеем y ( t ) – расчетный или оценочный процесс. В этой модели учтена только часть внешних и внутренних возмущений (факторов), следовательно, модель М 2приближенно описывает изменение параметров ее состояния во времени. Имея в виду сказанное, получим показатель научно-исследовательского риска.

Пусть параметр х проектируемого объекта ограничен сверху величиной х в доп (рис. 1.24). При этом справедливо x ≤ x в доп , а G 1есть область допустимых значений х. В качестве такого параметра могут выступать, например, километровый расход топлива q , перегрузка, угол атаки. Ограничение на х может быть и снизу, т. е. ограничение для минимального значения, например дальности полета L , прибыли инвестиционного проекта. При этом должно выполняться условие x ≥ x н доп , и область допустимых значений х есть G 2(рис. 1.25).

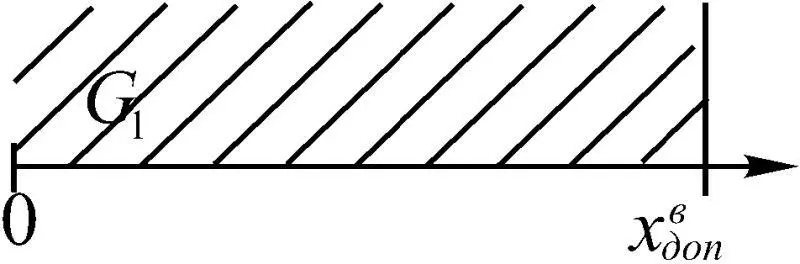
Рис. 1.24

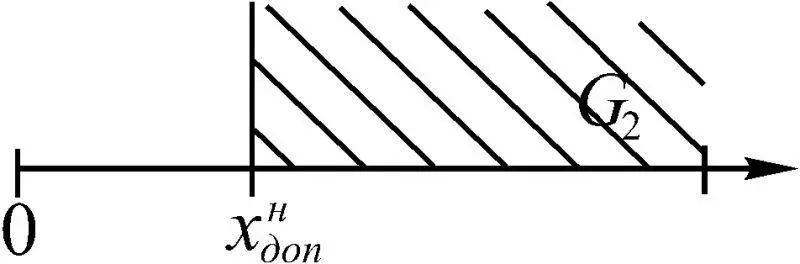
Рис. 1.25

При проведении научно-исследовательских работ параметры динамической системы выбираем таким образом, чтобы выполнялось условие x ≤ x в доп или x ≥ x н доп . Такой подход возможен, если х известно и детерминировано. Однако это не так в силу того, что объект (самолет) подвержен возмущающим факторам как внутреннего, так и внешнего происхождения. В этих условиях параметр состояния х представляет собой случайный процесс. При этом у имеет вид y ( t )= x ( t )+δ 1 x и также является случайным процессом, где δ 1 x – погрешность оценки. За счет δ 1 x мы обязаны ввести запас Δ в = x в доп – ( x o доп ) в или Δ н =( x o доп ) н – x н доп (рис. 1.26).

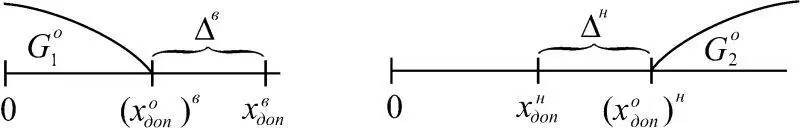
Рис. 1.26

В силу случайности δ 1 х, у, х возможен ряд событий, представляющих собой потери инвестора (случай ограничения сверху, например, по расходу топлива):

A 1=( x ≥ x в доп ; y ≤ ( x o доп ) в ), A 2=( x ≤ x в доп ; y ≥ ( x o доп ) в ),

A 3=( x ≥ x в доп ; у ≥ ( x o доп ) в ).

Вероятности этих событий

P 1= P ( A 1)= P ( x ≥ x в доп ; y ≤ ( x o доп ) в ),

P 2= P ( A 2)= P ( x ≤ x в доп ; у ≥ ( x o доп ) в ),