Владимир Живетин - Методы и средства обеспечения безопасности полета

Рис. 1.29

Как правило, траектория полета, соответствующая, например, максимальной дальности полета L , характеризуется совокупностью параметров, расчетные значения которых обозначим у 5= у опт =( у 51, у 52, …, у 5 m ) (рис. 1.30). Например, у 51= Н – расчетная (оптимальная) высота полета; у 52= M – расчетное (оптимальное) число Маха; у 53= G – вес самолета; у 54= х т – положение центра тяжести; у 55= K – числовое значение качества ( K = С у / С х ); С у , С х – коэффициенты подъемной силы и сопротивления. При этом L = f ( у опт )= f ( у 5).

В процессе полета задача состоит в обеспечении равенства у 4= у 5, где у 4=( у 41, у 42, …, у 4 m ), у 4 i – параметры траектории, измеренные с помощью бортового оборудования. Будем рассматривать также вектор у 3= у ф=( у 1ф, …, у m ф) фактических значений параметров траектории в данном полете в каждый из моментов времени t .

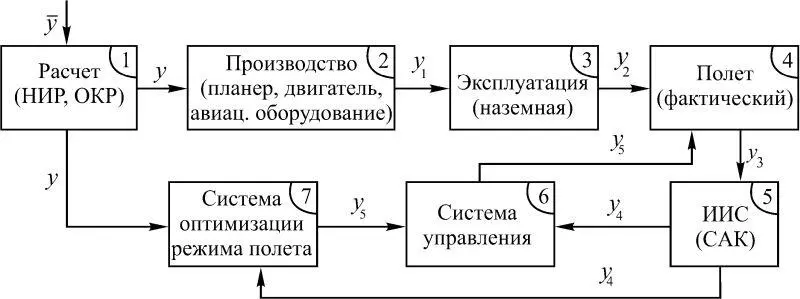
Рис. 1.30

На рис. 1.30 обозначения: ИИС – информационно-измерительная система, САК – система автоматического контроля.

Таким образом, выделены векторы (см. рис. 1.30):

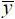– оптимальные параметры (при отсутствии погрешностей расчета);

у = у рас – расчетные оптимальные параметры траектории, полученные на этапе проектирования научно-исследовательских и опытно-конструкторских работ;

у 1= у п – параметры, реализованные с учетом погрешностей производства планера и двигателя ( с х , с у , …);

у 2 – параметры, реализованные с учетом предполетной подготовки;

у 3= у ф – фактические параметры траектории, реализованные в данном полете;

у 4= у изм – измеренные в полете параметры траектории;

у 5= у опт – оптимальные параметры траектории, полученные с помощью системы оптимизации режима полета (СОРП) в данный момент времени.

Согласно приведенной схеме, общая (суммарная) погрешность включает в себя следующие погрешности:

Δ y 0=( y – 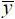) – методов расчета;

Δ у 1=( у 1– у ) – вносимые при производстве планера и двигателя;

Δ у 2=( у 2– у 1) – предполетной подготовки;

Δ у 3=( у 3– у 2) – обусловленные влиянием внешних возмущающих воздействий;

Δ у 4=( у 4– у 3) – вносимые системами измерения и контроля;

Δ у 5=( у 5– у 4) – связанные с несовершенством СОРП.

Таким образом, суммарная погрешность выдерживания (обеспечения) оптимальной дальности составляет .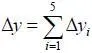

В полете с помощью систем ручного или автоматического управления вектор погрешностей Δ у стремятся свести к нулю. Запишем вектор Δ у иначе:

Δ у =Δ у пп +Δ у бо +Δ у вв +Δ у м +Δ у орт +Δ у э ,

где Δ у пп – погрешности по причине несовершенства производства планера и двигателя летательного аппарата; Δ у бо – погрешности измерения параметров траектории (погрешности бортового оборудования); Δ у вв – отклонения у , обусловленные внешними возмущениями; Δ у м – методическая погрешность выдерживания у из-за неточностей расчетных методов; Δ у э – погрешности, обусловленные эксплуатационными факторами, в том числе их неблагоприятным сочетанием; Δ у орт – погрешности, связанные с несовершенством СОРП.

При этих условиях необходимо разработать методику расчета численных величин показателей технического риска (инвестиционного риска), включающую построение моделей функционирования подсистем (1–7) (рис. 1.30), являющихся источниками отдельных компонент вектора погрешностей Δ у =(Δ у 1, …, Δ у 5) [18].

Способы решения задачи различны в случаях, если исследуемый ЛА находится на стадии проектирования или на стадии эксплуатации. В случае, когда ЛА находится в эксплуатации, есть возможность получить статистический материал о случайном процессе Δ у , например, в виде плотности вероятностей W (Δ у, t ). Однако при таком подходе невозможно вскрыть влияние отдельных подсистем (1–7) (рис. 1.30) на величину Δ у , т. е. оценить влияние производства, систем контроля, системы управления (в том числе пилота), следовательно, и их влияние на величину технического риска.

На этапе проектирования необходимо установить зависимость или построить математические модели между входами и выходами каждой из подсистем (1–7), а также модели погрешностей, порожденных каждой из этих подсистем. Полностью описать процессы от подсистемы (1) до подсистемы (7) достижения конечной цели полета – максимальной дальности – затруднительно, поэтому в некоторых моделях необходимо использовать результаты экспериментальных исследований для введения эмпирических соотношений в математические модели. Такой метод расчета численных величин показателей технического риска не позволяет получить окончательные результаты чисто теоретическим путем. Однако предлагаемый ниже метод дает возможность выделить задачи, которые решаются чисто расчетным или чисто экспериментальным путем, тем самым обеспечивая целенаправленное проведение экспериментальных исследований, а также уменьшение их объема.

Блок-схема совокупности систем, оказывающих влияние на потери инвестора, представлена на рис. 1.31 (СУ – система управления). Здесь рассматривается полет на максимальную дальность L max. Основная система автоматического контроля – САК-1, задачей которой является измерение фактических значений параметров траектории движения х ф в полете. С одной стороны, погрешности δ 1измерения х ф приводят к существенным потерям, например, расхода топлива, с другой – система автоматического контроля САК-2 регламентирует погрешности δ 2изготовления: обводов аэродинамических поверхностей конструкции ЛА, деталей двигателя и других систем самолета. В результате расчетная дальность полета L p = f 1( R* x , x , …), где расчетная величина сопротивления R* x определена без учета погрешностей δ 1, δ 2.