Владимир Живетин - Методы и средства обеспечения безопасности полета

А 3=( L ф < L кр , L р ≤ L доп ), А 4=( L ф ≥ L кр , L р > L доп ).

В результате искомые вероятности будут включать Р 1= Р ( А 1); Р 2= Р ( А 2); Р 3= Р ( А 3), Р 4= Р ( А 4). Вероятность Р 2соответствует тому, что мы отвергли экономически выгодную конструкцию (объект); Р 1 – приняли к исполнению вариант ЛА, который не подтверждает возможность достижения поставленной цели; Р 3 – получили отрицательный результат, что обусловило потери, связанные в данном случае с расходами проведения опытно-конструкторских работ; Р 4 – принято правильное решение.

Пусть ставятся следующие задачи: обеспечение одновременно оптимизации режимов пилотирования с целью снижения потерь расхода топлива, а также предупреждение критических режимов пилотирования с целью минимизации потерь техники и расходов на ремонт ее в послеаварийный период.

Пусть контролю и ограничению подлежат n параметров х 1, х 2, …, х n траектории полета самолета и состояния внутренних систем. В этом случае с помощью системы предупреждения критических режимов мы планируем осуществить предупреждение режимов полета, при которых параметры х i 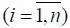принимают критические значения.

При этом финансовые (материальные) потери, обусловленные возникновением событий B i =( x i > x iкр ), где x iкр – критическое значение параметра x i , обозначим через α ip . В процессе проектирования мы можем оценить стоимость Ц i и массу m i такой системы. Управление расходом топлива 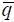будем осуществлять с помощью системы оптимизации режимов пилотирования. Суммарная стоимость ( Ц Σ) СПКР, СОРП и их масса ( m Σ) зависят от объема обрабатываемой информации, в том числе от количества контролируемых, ограничиваемых и управляемых параметров x j .

Итак, задача состоит в оптимизации ψ=(α*, 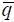, Ц Σ, m Σ). Трудность решения такой задачи заключается в том, что для минимизации (α*, 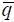) необходимо контролировать все параметры х i траектории полета, в том числе возмущающие факторы, например ветер. С другой стороны, для минимизации ( Ц Σ, m Σ) требуется ограничивать количество параметров х i 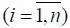. Это противоречие сегодня решается конструкторами ЛА, СПКР, СОРП путем анализа потребностей рынка и возможностей производственно-технологической базы авиастроения. Возможно, такой подход оправдан. Однако необходимо иметь аналитические методы, позволяющие проводить анализ технического риска.

Согласно приведенной схеме процесса создания и эксплуатации пассажирского самолета, необходимо обеспечить заданную величину прибыли Z 5= Z (рис. 1.11). В качестве критической величины прибыли выступает Z кр =0, т. е. когда прибыль равна нулю. В рамках рассматриваемой задачи прибыль Z зависит от расхода топлива ( 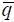) и потерь техники (α) в процессе эксплуатации самолета:

Z = f ( 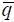, α).

Часто последнюю зависимость можно представить в более простом виде:

Z = k 1φ 1( 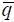)+ k 2φ 2(α),

где f , φ 1, φ 2 – непрерывные функции своих аргументов.

Если отклонение фактического расхода 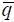от оптимального 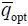мало, то возможно дальнейшее упрощение зависимости:

Z = k 3Δ 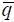+ k 4Δα,

где Δ 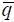= 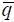– 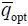; Δα=α – α opt.

Отметим, что частота P i выхода параметров траектории x i в критическую область позволяет вычислить α i = P i Ц i , где Ц i – стоимость работ по восстановлению техники, обусловленных выходом параметра x i в критическую область.

В процессе эксплуатации самолета, оборудованного СОРП и СПКР, возможны следующие события [18]:

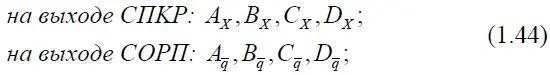
где

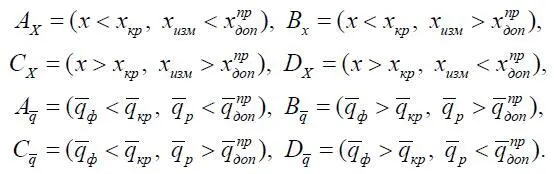
При этом 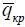есть критическое значение расхода топлива, начиная с которого полет совершается без прибыли, бизнес несет финансовые потери, прибыль Z или равна нулю, или отрицательная; 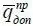– допустимая величина расхода, отличающаяся от 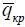на некоторый запас, обусловленный влиянием погрешностей бортовых измерительных систем и систем оптимизации.

Введем событие A 1( Z ), которое происходит тогда, когда выполняются одновременно два события А 1=( А X , 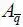). Обозначим через Р 1вероятность такого события, и тогда

P 1= P ( A X , 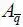)= P ( A X )+ P ( )

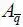в силу независимости А X и 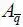из соотношения (1.44).

Вероятность Р 1( А 1) является характеристикой безопасного состояния в полете по функционально-экономическому параметру. На практике возможны различные сочетания событий из соотношений (1.44) вида

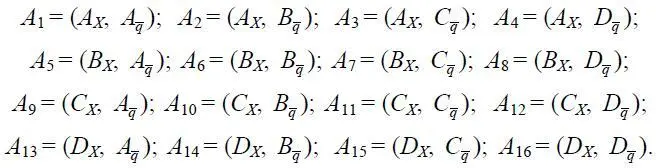
Для части А i 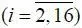характерно событие Z < Z кр , где прибыль Z в соответствующем режиме полета будет критической. Другие А i включают события, при которых мы отказались от выгодного (оптимального) режима. Каждому событию А i 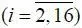соответствует своя вероятность P i = P ( A i ). В силу независимости A i между собой вероятность суммы всех событий A i имеет вид

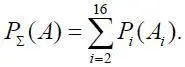
Задача проектировщика состоит в том, чтобы подобрать такой комплекс: ЛА, двигатель, СПКР, СОРП, для которого вероятность Р 1достигала бы максимума, а вероятность 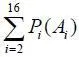– минимума.