Владимир Живетин - Методы и средства обеспечения безопасности полета
- Название:Методы и средства обеспечения безопасности полета
- Автор:
- Жанр:
- Издательство:Изд-во Института проблем риска, Информационно-издательский центр «Бон Анца»
- Год:2010
- Город:Москва
- ISBN:978-5-98664-055-6, 978-5-903140-39-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Живетин - Методы и средства обеспечения безопасности полета краткое содержание
Методы и средства обеспечения безопасности полета - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
С учетом сделанных выводов решение (1.31) запишем в виде
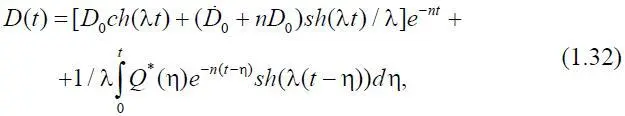
где ch ( · ) и sh ( · ) – гиперболические косинус и синус соответственно. Первое слагаемое D 1( t )=[ D 0 ch (λ t )+( 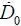 + nD 0) sh (λ t ) / λ] e – nt в терминах теории систем описывает свободные колебания, что для микроавиационной системы означает изменение оборотного капитала. В силу устойчивости системы (1.31) эти изменения удовлетворяют следующим условиям:
+ nD 0) sh (λ t ) / λ] e – nt в терминах теории систем описывает свободные колебания, что для микроавиационной системы означает изменение оборотного капитала. В силу устойчивости системы (1.31) эти изменения удовлетворяют следующим условиям:
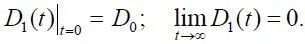
С их учетом второе слагаемое D 2( t ) в (1.32) примет форму
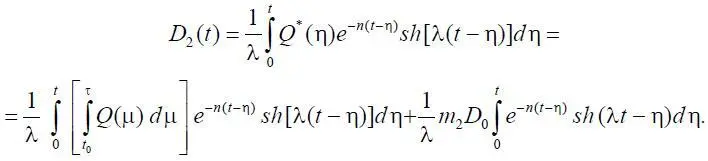
Условия прибыльности и убыточности
Определим, при каких ограничениях, накладываемых на параметры системы, и каких управлениях имеют место:
– прибыльность 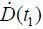 > 0, где t 1 – момент времени, начиная с которого микроавиационная система начала давать прибыль;
> 0, где t 1 – момент времени, начиная с которого микроавиационная система начала давать прибыль;
– убыточность 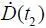 < 0, где t 2 – момент времени, начиная с которого микроавиационная система стала убыточной;
< 0, где t 2 – момент времени, начиная с которого микроавиационная система стала убыточной;
– крах [ K y ( t 0)+ D ( t 3)] ≤ 0, где t 3 – момент времени, начиная с которого капитал K y ( · ) за счет оборотных средств D ( t 3) стал нулевым или отрицательным.
Очевидно, что для различных значений времени микроавиационная система может быть прибыльной либо убыточной до тех пор, пока не произойдет третье событие, означающее разорение микроавиационной системы и прекращение ее существования.
Определим условия, при которых микроавиационная система является прибыльной. Для этого рассмотрим (1.32) и представим 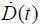 при нулевых начальных условиях в виде
при нулевых начальных условиях в виде
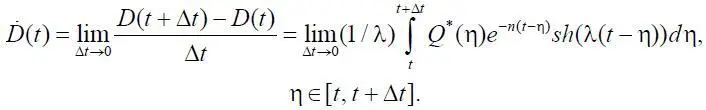
Поскольку в данном выражении подынтегральная функция положительна, условие 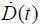 > 0 выполняется, если Q *(μ) > 0. Очевидно, при этом Q* ( t ) > 0 и, следовательно,
> 0 выполняется, если Q *(μ) > 0. Очевидно, при этом Q* ( t ) > 0 и, следовательно,

Осуществим в последнем неравенстве замену
Q ( t )=( B 1– B 2) 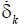 ( t ) – ( B 1 a 2– B 2 a 1)δ k ( t ),
( t ) – ( B 1 a 2– B 2 a 1)δ k ( t ),
при этом получим неравенство
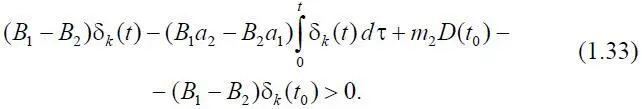
Задача анализа прибыльности микроавиационной системы заключается, таким образом, в выборе такой совокупности параметров δ k ( t ), τ, τ 0, P 1, γ 1, γ 2, γ 3, γ 4, γ 5, при которой выполняется условие (1.33).
Процентная компенсация возможных технико-экономических потерь
Реальная возможность риска, возникающего при осуществлении пассажироперевозок микроавиационной системой обусловливает необходимость повышать процентную ставку П* (1.7) до значения П* 1, зависящего от уровня риска потерь технико-экономического потенциала, который определяется вероятностью пропуска опасной ситуации или критической ситуации Р 4, которая будет введена в главе II, и в дальнейшем будет представлен метод ее расчета. Итак, вероятность Р 4характеризует потери техники в аварии, катастрофе.
Приведем необходимые функциональные соотношения (математическую модель) учета вероятности Р 4при расчете процентной ставки П * в момент его выдачи, т. е. экономический эквивалент, компенсирующий риск системы.
Представим возвратные средства D в в виде
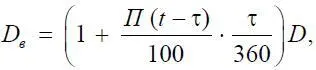
где 360 – условное количество дней в году.
Обозначим через p i вероятность, с которой в микроавиационную систему может поступить сумма D вi , составляющая k% от величины D в.
Величина D вi представляет собой дискретную случайную величину, принимающую возможные значения D в 1 , D в 2, …, D вn с вероятностями p 1, p 2, …, p n , 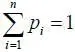 . Математическое ожидание M [ D в ] вычисляется по известной формуле
. Математическое ожидание M [ D в ] вычисляется по известной формуле

Выделим частный случай, когда n =2, причем величина D в принимает свои граничные значения: полный возврат и полный невозврат. Вероятности этих двух событий равны соответственно (1 – P * 4) и P* 4. При этом, как следует из (1.34),
M [ D в ]=(1 – P* 4) D в + P* 4 · 0,
а формула для суммы средств, возвращаемых в микроавиационную систему, примет следующий вид:
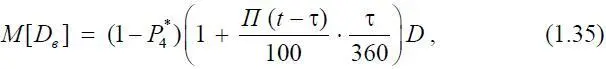
где D – исходная величина финансовых средств (кредита); P* 4 – вероятность невозврата финансовых средств; П ( t – τ) – процентная ставка, назначенная с учетом его потерь; τ – срок возврата кредита (в днях). В дальнейшем будем называть D финансовыми средствами или кредитом, полученным эксплуатирующей организацией.
Отметим, что P* 4= P 4 · P' 4, где P' 4 – вероятность того, что D ( t ) пропали во время реализации проекта, чему соответствует событие D в ( t ) ≤ 0. Здесь имеет место вероятность P 4, подлежащая вычислению.
В условии отсутствия риска кредит возвращается микроавиационной системе с процентами, ставка которых равна П 0( t – τ). При этом общая сумма возвращаемых средств D в 0выражается следующей зависимостью:
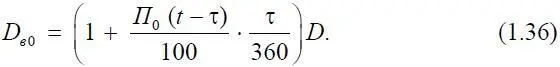
Компенсация потерь, связанных с опасностью невозврата заемщиком кредита в данной сделке, имеет место при наличии условия M [ D в ]= D в 0. Воспользовавшись для данного равенства формулами (1.35) и (1.36), получим
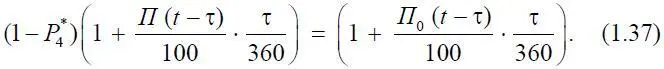
Введем обозначения
Читать дальшеИнтервал:
Закладка:










