Владимир Живетин - Методы и средства обеспечения безопасности полета

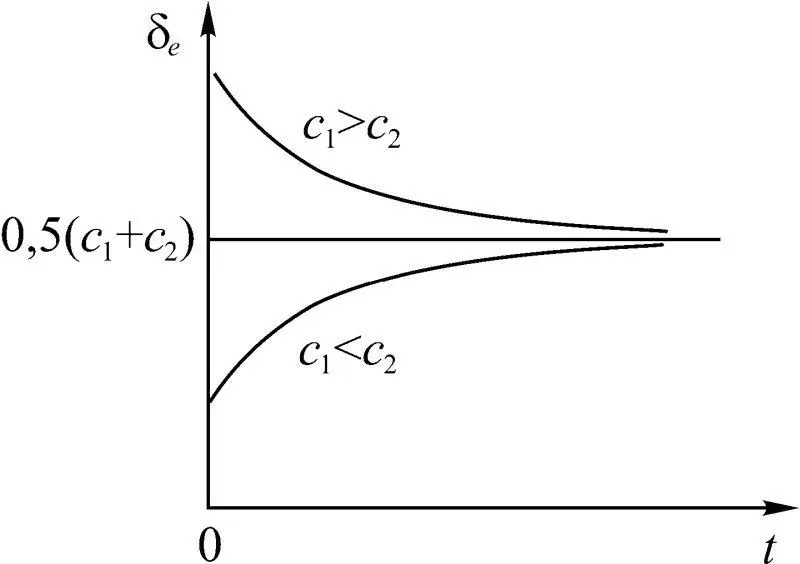
Рис. 1.18

При этом независимо от того, какое из неравенств – δ e (0) > ( c 1+ c 2) / 2 или δ e (0) < ( c 1+ c 2) / 2 – имело место, с увеличением t соотношение (1.21) становится более точным.

Поведение системы меняется при b ≠ 0. Если при этом условии a > 0 и c > 0, то для больших t , согласно (1.20), имеет место приближенная зависимость δ e ( t ) ≈ (( c 1+ c 2) / 2)exp[–( a – 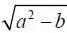) t ]. Здесь возможны следующие две ситуации: ( a – 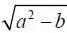) > 0 и ( a – 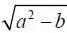) < 0. Условие ( a – 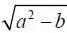) > 0 выполняется при b > 0, тогда δ e уменьшается с увеличением t , что говорит о снижении кредитоспособности микроавиационной системы. В противном случае, когда b < 0, кредитоспособность микроавиационной системы с течением времени возрастает (рис. 1.19). Отсюда следует, что условие b =0 при Δ > 0 характеризует критическое состояние, разделяющее области увеличения и падения кредитоспособности микроавиационной системы.

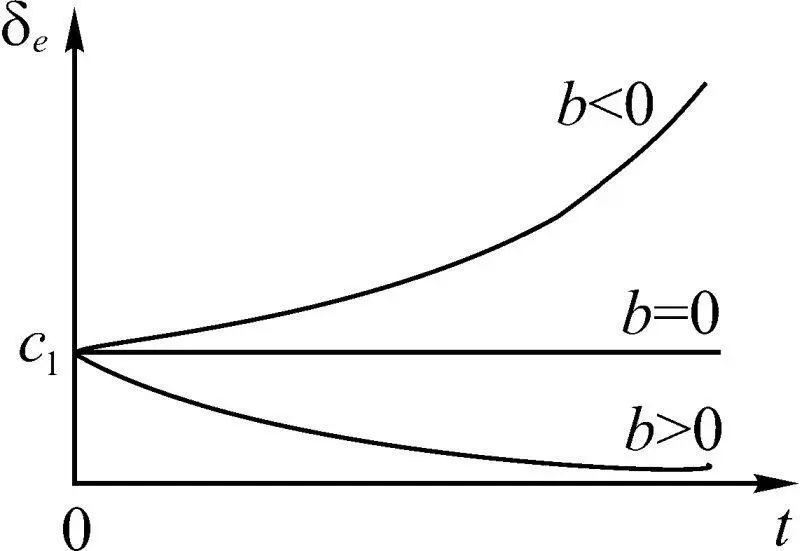
Рис. 1.19

При Δ < 0 корни характеристического уравнения (1.18) являются комплексными, и общее решение уравнения (1.17) записывается в виде

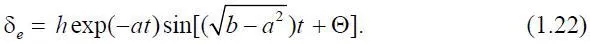
Постоянные h и Θ определяются из начальных условий по формулам

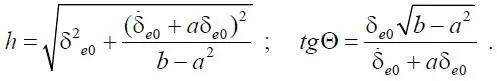
Из (1.22) следует, что в начальный момент времени микроавиационная система является кредитоспособной при выполнении неравенства δ e (0)= h sinΘ > 0. Однако выполнение этого условия не означает сохранение кредитоспособности микроэкономической системы при любом t > 0. Как следует из (1.22), процесс изменения δ e является колебательным с уменьшением амплитуды во времени (рис. 1.20). Поэтому при t , стремящемся к бесконечности, δ e ( t ) стремится к 0, что говорит о падении кредитоспособности микроавиационной системы. Кроме того, в силу колебательного характера процесса для некоторых моментов времени t n , n =1,2,…, выполняется условие δ e ( t n )=0.

Таким образом, микроавиационная система обладает кредитоспособностью при любом значении t , если b < 0, поскольку при этом параметры банка γ и П * таковы, что (1 – γ)(1+ П *) > 1 и Δ ≥ 0. В противном случае кредитоспособность микроавиационной системы со временем падает.

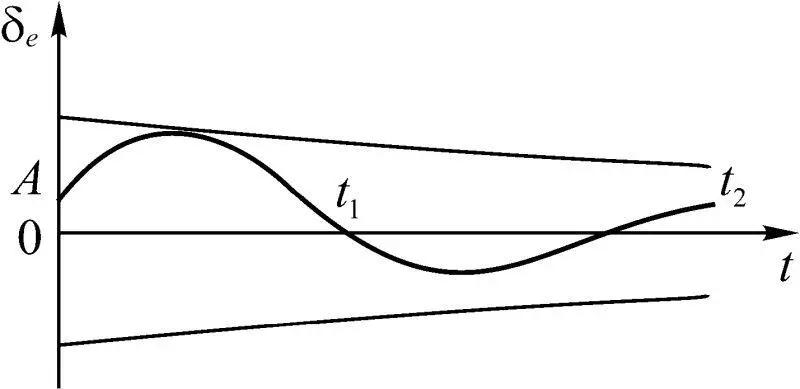
Рис. 1.20

Пример. Пусть при t =0 дано следующее начальное состояние: δ e 0=10 4 руб., =0. Согласно модели, микроавиационная система характеризуется параметрами τ D , τ k , П * , γ. Примем, что поступившие в данный момент времени денежные средства на различные цели полностью израсходуются через 6 суток. Тогда τ D =2 сут. Кредит выдается на 30 суток, тогда τ k =10 сут.

Пусть П =40 %, тогда П *=1/30. Параметр γ рассмотрим как управление. Он определяет долю изымаемых из оборота денег. Выбирая разные значения γ, получим разное поведение финансовых потоков микроавиационной системы. Сначала найдем значение γ, соответствующее равновесному функционированию банка, при котором δ e =δ e 0=const. Согласно формуле (1.15), найдем γ= П */(1+ П *)=1/31. Таким образом, примерно 3,226 % денег используется в разных целях, а 96,774 % выдается в кредит. При этом микроавиационная система не расширяется, не разоряется, а находится в равновесном состоянии.

Далее рассмотрим два случая: γ=γ (1)=0,05 и γ=γ (2)=0,01. При этом a =0,3; b = b (1) 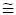0,000917; b = (2) 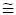0,001150. Соответствующие значения корней характеристического уравнения (1.18)

λ (1) 1 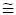–0,0015; λ (1) 2=–0,5985, λ (2) 1=–0,6019; λ (2) 2=+0,0019.

В первом случае процесс описывается формулой

δ e =10 4(1,0025 e –0,0015 t – 0,0025 e –0,5985 t ),

где время t измеряется в сутках. При этом величины δ e , следовательно, δ n – убывающие и стремятся к нулю при t → ∞. Это означает, что микроавиационная система через некоторое время разорится.

Во втором случае процесс описывается функцией

δ e =10 4(0,9918 e –0,6019 t +0,0032 e 0,0019 t )

Здесь первое слагаемое величины δ e быстро убывает, а второе медленно, но возрастает. Оба слагаемых положительные. Поэтому, хотя вначале величина δ e будет убывать, и состояние микроавиационной системы будет ухудшаться, через некоторое время она начнет расширять свою деятельность. Параметры δ e и δ n будут возрастать.

Дополнив соотношения (1.3) дифференциальным уравнением (1.13), получим следующую систему уравнений:

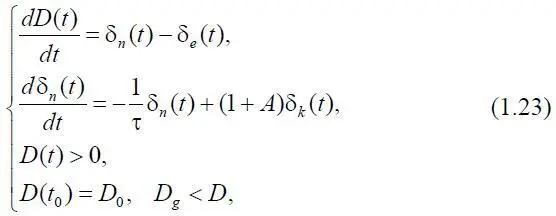
где (1+ A )=(1+ П* ) / τ, δ k ( t )=δ p ( t ). Отметим, что при заданном значении δ k ( t ) система (1.23), состоящая из двух дифференциальных уравнений, содержит три неизвестные функции: D ( t ), δ n ( t ), δ e ( t ), являясь, таким образом, незамкнутой. Это означает, что для ее решения, в частности, необходимо задать δ e ( t ). Однако в этом случае исключается возможность проведения всестороннего анализа кредитной политики. Поэтому предлагается пойти по следующему пути.

Система (1.23) включает в себя величину δ k ( t ), т. е. кредитный поток, который может быть реализован по распоряжению руководства микроавиационной системы. При максимальном использовании финансовых ресурсов микроавиационной системы поток δ k ( t ) включает в себя поток возвратного кредита, а также часть прибыли и имеет, таким образом, следующий вид:

δ k ( t )=δ k ( t – τ)+γ 1 A δ k ( t – τ),

где A δ k ( t – τ) – прибыль в виде процентов по кредиту, отданных при ( t – τ), γ 1 – коэффициент, характеризующий ту часть прибыли, которая отдана в кредит в момент времени t. Изменяя коэффициент γ 1, можно получать различные значения δ k ( t ). При этом γ 1< 1, поскольку расходная часть δ e ( t ) включает в себя и другие компоненты.