Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

В 30-х годах круг исследователей, занимающихся проблемами квантовой химии, несколько расширился — появились работы Румера, Вейля, Борна, Теллера и др. В результате была разработана общая теория возмущений по межэлектронному взаимодействию, при этом также широко использовалась теория групп перестановок (метод Гайтлера-Лондона-Румера-Вейля). В основе теории геттингенских авторов лежали следующие рассуждения.

Многоатомная молекула рассматривалась ими как единая многоэлектронная система. Состояния электронов в отдельных атомах (А, В, С ...) описывались одноэлектронными функциями φ i A( r), φ j B( r) и т. п. Многоэлектронную функцию системы при отсутствии взаимодействия между атомами можно представить в виде произведения этих одноэлектронных функций:

(3.18)

Ввиду неразличимости электронов, помимо функции (3.18), можно написать еще ряд функций, полученных из нее перестановкой координат электронов. Всего, таким образом, мы получим ЛМ функций. При учете взаимодействия между атомами все эти функции можно использовать в качестве нулевого приближения в теории возмущений. Многоэлектронные функции молекулы должны представляться их линейными комбинациями, коэффициенты которых определяются секулярными уравнениями порядка N\. Так как для систем, представляющих химический интерес, порядок соответствующих секулярных уравнений становится чрезвычайно большим, необходимо использовать любую возможность для его уменьшения путем деления рассматриваемой секулярной задачи на более простые. Как было показано работами Гайтлера, Румера и Вейля, эта задача может быть решена в значительной степени с учетом перестановочной симметрии и принципа Паули. При этом разрабатывался математический аппарат, соответствующий теории спин-валентности. Для большинства молекул в их основных состояниях полный спиновый момент имеет нулевое значение. Учитывая, что операторы спинового момента действуют на спиновые переменные отдельных электронов, а не на их пространственные координаты, можно представить многоэлектронные функции в виде произведения двух сомножителей, один из которых зависит только от пространственных, а другой только от спиновых переменных. Последний может быть построен из одноэлектронных спиновых функций а и р, удовлетворяющих уравнениям

(3.19)

где — оператор проекции одноэлектронного спинового момента на ось квантования z. Так, например, для молекулы водорода, включающей два электрона, как было показано Гайтлером и Лондоном, можно построить четыре двухэлектронные спиновые функции:

(3.20)

(3.21)

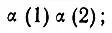(3.22)

(3.23)

Только первая из этих функций соответствует синглетному состоянию и инвариантна по отношению к повороту осей квантования, так как при любом их выборе проекция нулевого спинового момента равна нулю. Поэтому эта функция, обозначаемая как [β], была названа Вейлем спин-инвариантом.

При рассмотрении более общего случая молекул с любым четным числом электронов многоэлектронная спиновая функция χ(σ 1,...,σ N) строилась в виде произведения таких спин-инвариантов. Как и в случае построения функций Ф( r 1 ,..., r N ), в силу неразличимости электронов можно построить множество функций (многоэлектронных спин-инвариантов) χ(σ 1,...,σ N), отличающихся перестановкой электронов или так называемой схемой спинового спаривания. Эти функции, как правило, образуют линейно-зависимый набор, т. е. некоторые из них являются линейными комбинациями остальных и должны быть исключены из рассмотрения. Формула, определяющая число линейно-независимых функций, была получена Румером [76]. Им же было предложено графическое правило, позволяющее выявить и устранить линейные зависимости между функциями, полученными путем спинового спаривания. Согласно правилу Румера, каждой одноэлектронной спиновой функции следует сопоставить точку на плоскости, расположив точки таким образом, чтобы они лежали на окружности или на другой выпуклой кривой. Затем эти точки соединяются друг с другом штрихами, каждый из которых является графическим представлением определенного простейшего спин-инварианта. Как показал Румер, многоэлектронные функции, соответствующие диаграммам с непересекающимися штрихами, линейно независимы, а остальные содержащие, по крайней мере, одно пересечение, являются, их линейными комбинациями.

В качестве примера можно привести шестиэлектронную систему. В этом случае можно составить пять диаграмм Румера с непересекающимися штрихами (рис. 13, а). Им соответствуют следующие спин-инварианты:

(3.24)

Функция 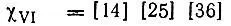(рис. 13,б) будет представлять собой линейную комбинацию функций (3.24):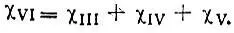

Рис. 13. Диаграммы Румера: а — с непересекающимися и б — с пересекающимися штрихами для молекулы бензола

К сожалению, правило Румера применимо лишь в том случае, когда число электронов не слишком велико. Если учитывать электроны атомов, образующих молекулу, то оно оказывается практически неприемлемым [11] Позднее, в 1937 г., была сформулирована более общая методика построения линейно-зависимых наборов спиновых функций с использованием таблиц Юнга. . Но иногда в рассмотрение включается лишь часть электронов. Например, при изучении плоских органических молекул часто ограничиваются учетом только одной π-орбитали от каждого атома. Именно в этом случае правило Румера нашло применение.