Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

В заключение этого параграфа остановимся на месте понятия гибридизации в логической структуре метода ВС. Использование гибридных орбиталей является необходимым условием представления многоэлектронной функции молекулы одной структурой (приближение идеального спаривания). Иными словами, концепция гибридизации позволяет наиболее просто интерпретировать классические структурные формулы в терминах метода ВС и в этом смысле она альтернативна концепции резонанса.

Кроме того, гибридные орбитали образуют оптимальный базис для представления локализованных молекулярных орбиталей. Таким образом, концепция гибридизации оказывается полезной при согласовании квантовомеханического описания молекул с их описанием в рамках классической теории строения.

Концепция (или теория) резонанса была предложена Полингом в начале 30-х годов. Основная идея ее заключалась в следующем. Если Ψ 0представляет некоторую волновую функцию системы, то интеграл 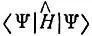(Н ^— оператор Гамильтона) должен быть больше или равен энергии наинизшего состояния Е 0. Чем ближе Ψ к этой собственной функции, тем меньше будет разность Е — Е 0. Допустим, что мы нашли функцию Ψ 1, которая представляет возможные состояния системы, например состояние, соответствующее некоторой электронной формуле Льюиса. Тогда при замене Ψ на Ψ 1в указанном интеграле можно рассчитать электронную энергию E 1, как функцию от межъядерных расстояний. Аналогично функция Ψ 2, соответствующая альтернативной электронной формуле, может быть использована для расчета Е 2. Если уровень Е 1лежит значительно ниже уровня E 2, то функция Ψ 1будет лучше аппроксимировать основное состояние системы, чем Ψ 2, и если другие альтернативы отсутствуют, то можно принимать во внимание только электронную формулу, соответствующую Ψ 1. Вообще говоря, если Ψ 1и Ψ 2имеют одинаковый характер симметрии и, что особенно важно, одинаковую мультиплетность (т. е. одно и то же число неспаренных электронов), то может быть найдено значение E, соответствующее функции aΨ 1+ bΨ 2. Когда Е 1и E 2не очень различаются и когда члены, соответствующие взаимодействию между состояниями Ψ 1и &Ψ 2велики, то оказывается, что функцией, дающей наилучшее приближение к собственной функции основного состояния системы, будет не Ψ 1и не Ψ 2, а их линейная комбинация с коэффициентами а и b, являющимися величинами одного порядка. В этом случае ни одна электронная формула сама по себе не может быть сопоставлена молекуле. Необходимы обе структуры, хотя одна из них, возможно, будет иметь больший вес, чем другая. "Молекула,- отмечает Полинг,- могла бы рассматриваться как быстро флуктуирующая между двумя электронными формулами, и ее стабильность получается большей, чем для любой из этих формул благодаря "энергии резонанса этих флуктуации" [72, с. 996-997]. Впоследствии теория резонанса была развита Полингом, Уэландом и другими авторами, которые применили ее к широкому кругу химических соединений.

Достаточно подробно генезис этой теории был рассмотрен в монографии Г. В. Быкова [5]. Поэтому, избегая повторений, мы остановимся в дальнейшем только на тех вопросах, которые не были должным образом освещены в литературе.

Наибольшее распространение концепция резонанса нашла в органической химии. При этом популярность ее была так велика, что она часто отождествлялась с методом ВС. Когда же гипертрофирование роли резонанса электронных структур было подвергнуто критике, такое отождествление отрицательно сказалось на отношении многих химиков к методу ВС и привело к неправильному пониманию роли и логической структуры последнего. Историческое значение концепции резонанса состоит, во-первых, в том, что она определила одно из возможных направлений развития метода ВС. Во-вторых, она позволила глубже понять соотношение между классической и квантовой теориями строения химических соединений, вскрыв те стороны физической и химической реальности, которые не могли быть адекватно отражены классической теорией строения.

Чтобы яснее представить роль резонанса в логической структуре этого метода, попытаемся ответить на следующий вопрос: возможен ли "безрезонансный" метод ВС, и если да, то каковы будут его особенности. С ретроспективной точки зрения иной возможный путь развития метода ВС мог состоять в сохранении приближения идеального спаривания, но при этом пришлось бы обобщить концепцию гибридизации, т. е. использовать в качестве базисных функций не атомные, пусть даже гибридные (в обычном смысле слова) орбитали, а их линейные комбинации, вообще говоря, не ортогональные [19] Базисные АО в обычной формулировке метода ВС также не ортогональны. . Уравнениями, определяющими эти линейные комбинации, являются уравнения Годдарда [43]. В некотором смысле этот метод, названный Годдардом "обобщенным методом ВС", является одновременно и обобщением метода МО. Иными словами, концепция резонанса служила не только одним из способов выражения метода ВС, который придал мышлению химиков большую гибкость, но и явилась своеобразным водоразделом, отделяющим два наиболее распространенных метода квантовой химии, ВС и МО,так как "безрезонансный" вариант метода ВС представляет собой такую модификацию последнего, которая придает ему черты метода МО.

Проиллюстрируем этот тезис на примере молекулы бензола. В методе ВС для описания π-электронной системы молекулы бензола необходим учет пяти независимых структур, характеризуемых диаграммами I-V (см. рис. 16). Эти диаграммы могут быть построены с использованием схем и таблиц Юнга.

Антисимметричная собственная функция оператора может быть получена из произведения координатной Φ и спиновой Χ функций действием оператора Годдарда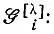

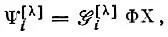(3.50)

где

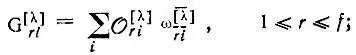(3.51a)

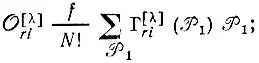(3.51б)

(3.51в)

где 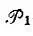— операторы перестановки пространственных координат; 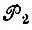— операторы перестановки спиновых переменных; 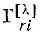— матричные элементы неприводимого представления [λ] группы перестановок N-электронов; f — размерность этого представления.