Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

1. Одноэлектронные уровни характеризуют энергию отдельных электронов, но не полную электронную энергию молекулы, которая отлична от суммы одноэлектронных. Взаимодействие замкнутых электронных оболочек приводит к расщеплению соответствующих одноэлектронных уровней, и хотя это расщепление практически не приводит к упрочению химической связи, оно может проявляться в спектрах молекулы.

2. Безусловно, ошибочным является исключение из рассмотрения разрыхляющего уровня, когда он заполнен только одним электроном, т. е. предположение о невозможности образования трехэлектронных связей, характеризуемых диаграммой вида

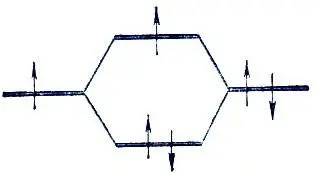
Существование таких связей с точки зрения простого метода Гайтлера-Лондона невозможно, но в действительности они реализуются (например, в ионе Не + 2и т. п.).

Историческая роль работы Леннард-Джонса состоит в том, что, во-первых, сопоставление одноэлектронных состояний в молекуле с соответствующими одноэлектронными состояниями разъединенных атомов и приписывание молекулярным электронам квантовых чисел образующих молекулу атомовзаложило фундамент для развития метода МО ЛКАО — основного метода современной квантовой химии. Во-вторых, Леннард-Джонсом была высказана идея о разделении всех молекулярных электронов на электроны внутренних, замкнутых атомных оболочек и валентные электроны, определяющие в основном химические свойства молекулы аналогично тому, как это делалось в методе ВС. Эта идея используется, в частности, в современных полуэмпирических методах квантовой химии.

Фундаментальное значение для разработки теории многоэлектронных систем имели работы Хартри, Гоунта и Фока, в которых был сформулирован метод самосогласованного поля (ССП). Основная идея этого метода по Хартри [47] состояла в том, что каждому электрону атома сопоставлялась некоторая одноэлектронная функция (орбиталь), аналогично тому, как в полуклассической теории атома Бора-Зоммерфельда предполагалось, что каждый атомный электрон движется по определенной орбите. Следует отметить, что в рамках квантовоме-ханической теории молекулярных спектров эта идея независимо развивалась Хундом и Малликеном, которые, однако, не предприняли попыток вычисления одноэлектронных функций, ограничиваясь, как мы видели выше, их классификацией по симметрии и энергии посредством задания соответствующих квантовых чисел.

Хартри опирался на трактовку одноэлектронной волновой функции ψ, данную Шредингером и развитую затем Клейном, согласно которой квадрат модуля |ψ| 2дает объемную плотность распределения электрического заряда в состоянии, описываемом функцией ψ. Отмечая, что такая интерпретация не является бесспорной, Хартри указывает в то же время, что она позволяет построить физически разумную модель как для стационарных состояний электронных оболочек атомов, так и для процессов излучения [28] Правильная вероятностная интерпретация физического смысла волновой функции была дана Борном в 1926 г. и вскоре стала общепринятой. . Принимая во внимание доказанную ранее Унзольдом теорему о сферической симметрии распределения заряда в замкнутых оболочках атомов, Хартри отмечает, что приближение центрального поля в квантовой механике является более удовлетворительным, чем в старой квантовой теории.

Хартри показал далее, что указанные допущения (одноэлектронное приближение и приближение центрально-симметричного поля) позволяют свести задачу к одномерному уравнению, определяющему движение одного электрона в центрально-симметричном некулоновском поле, создаваемом ядром и всеми прочими электронами:

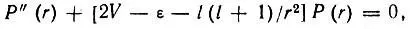(3.58)

где введенная Хартри радиальная функция Р(r) определяет радиальную плотность заряда на расстоянии г от ядра, т. е. P 2dr при соответствующей нормировке функции Р является зарядом, локализованным в пространстве между двумя сферами радиусов r и r+δr; V — потенциал притяжения рассматриваемого электрона к ядру (с учетом его отталкивания от других электронов); величинае характеризует энергию электрона в состоянии, определяемом функцией Р; l — квантовое число орбитального момента импульса.

Основная трудность решения уравнения (3.58) состояла в том, что потенциал V определяется через искомые функции Р, так что уравнение оказывается нелинейным.

Хартри разработал метод решения таких уравнений, названный им процедурой самосогласования. Согласно этому методу сначала задается некоторое исходное поле (initial field) , затем в это поле вносится поправка, учитывающая то, что данный электрон взаимодействует лишь с другими электронами, но не сам с собой, в результате чего получается соответствующий исходному полю потенциал V. С этим потенциалом уравнение (3.58) решается как линейноеотносительно Р. Соответствующее вычисленным радиальным функциям распределение заряда в атоме обусловливает новое поле, являющееся конечным для данной итерации процедуры самосогласования. Если это конечное поле достаточно близко к исходному, то решение уравнения (3.58) считается завершенным. В противном случае процедура повторяется с использованием конечного поля предыдущей итерации в качестве исходного поля последующей. Таким образом, процедура самосогласования может быть охарактеризована приводимой ниже диаграммой:

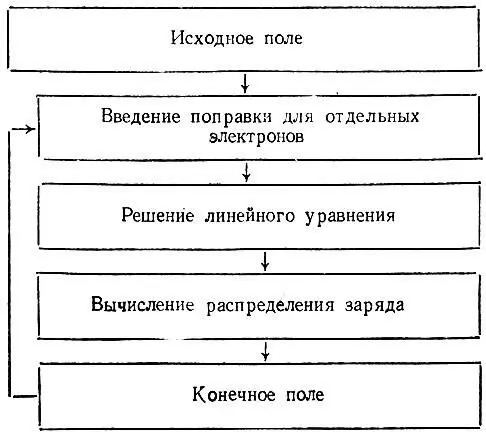
Разработанный им метод Хартри иллюстрировал расчетами для атома Не и ионов 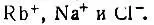. Выбор объектов не случаен, ибо теория была сформулирована лишь для атомов и ионов с замкнутыми оболочками. Кроме того, в ней не фигурирует явно полная многоэлектронная функция, методы построения которой были развиты позднее.

Теория Хартри, как было впервые показано Гоунтом в феврале 1928 г. [41], соответствует представлению полной N-электронной функции в виде простого произведения одноэлектронных функций

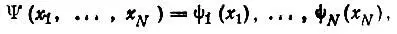(3.59)

где x i— совокупность пространственных (x i, y i, z i) и спиновой (σ i) переменных для i-го электрона.

Гоунт подчеркивает, что "полная волновая функция должна быть антисимметричной относительно любой перестановки пространственных и спиновых координат двух электронов, тогда как функции, не включающие спиновые переменные, могут иметь различный характер симметрии" [41, с. 329]. Простая же мультипликативная функция (3.59), очевидно, не удовлетворяет сформулированному условию антисимметрии. Гоунт показал, что в первом приближении полную антисимметричную функцию системы N электронов можно аппроксимировать суммой