Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

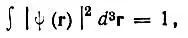(4.2)

то такому же условию нормировки будет удовлетворять волновая функция ψ'(r). Математические ожидания всех физических величин, представленных операторами 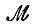и вычисляемых как интегралы

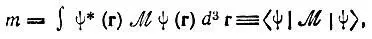(4.3)

также не меняются при рассматриваемом преобразовании. Именно это обстоятельство и доказывает, что волновые функции ψ и ψ' описывают одно и то же состояние частицы.

Действие оператора 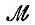на ψ(r) определяется по формуле

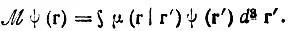(4.4)

Функция μ в (4.4) называется ядром оператора 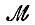в его интегральном представлении. При таком представлении операторов 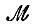легко видеть, что математическое ожидание

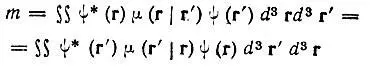(4.5)

определяется фактически не функцией ψ(r), а произведением двух ψ-функций

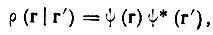(4.6)

которое называется матрицей плотностидля частицы, нахо дящейся в определенном состоянии. Строго говоря, матрица плотности ρ( r|r') не может быть матрицей в обычном смысле этого слова, если координаты r, нумерующие ее строки, и координаты r', нумерующие ее столбцы, не дискретны. Тем не менее термин "матрица плотности" для ρ( r|r') является общепринятым.

Матрица плотности становится истинной матрицей, если она представлена в некотором базисе функций X k( r), т. е. определяется совокупностью матричных элементов P kl, по которым можно воспроизвести ρ( r|r') согласно равенству

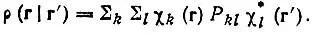(4.7)

В качестве функций X k( r) в квантовой химии чаще всего используются атомные орбитали, центрированные на ядрах атомов, образующих молекулу. Например, для молекулы Н 2 +матрица плотности в двухцентровом базисе 1s-орбиталей атомов водорода имеет вид

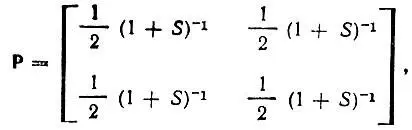
где S — интеграл перекрывания базисных АО.

Матричные элементы Р klполучаются из коэффициентов разложения МО в базисе АО:

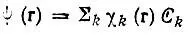
по формуле

Зависимость матрицы плотности ρ( r|r') от rи r'не следует понимать в том смысле, что она зависит от координат двух частиц.

В действительности rи r'представляют собой две различные (но возможно и совпадающие) точки пространства, в которых может быть локализована одна рассматриваемая частица. При этом плотность вероятности локализации ее в некоторой точке rравна диагональному элементу 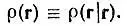. Именно эту функцию характеризуют часто используемые в квантовой химии карты распределения электронной плотности. Функция ρ( r) содержит информацию, достаточную для вычисления математических ожиданий тех весьма многочисленных физических величин, операторы которых не включают интегрирования или дифференцирования. Например, дипольный момент d электронной системы относительно центра координат представлен одноэлектронным оператором с ядром [33] Функция Дирака σ(r — r') относится к классу так называемых обобщенных функций и определяется равенством ) :

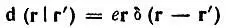(4.8)

и определяется по формуле

(4.9)

Использование матрицы плотности вместо волновой функции устраняет указанную выше неоднозначность в квантовомехани-ческом описании состояния частицы. В то же время такое описание является более общим и позволяет характеризовать одночастичные состояния для систем, содержащих несколько различных или тождественных частиц, хотя точное описание этих состояний с помощью волновых функций невозможно.

Пусть некоторое состояние W-электронной системы задано антисимметричной нормированной функцией Ψ(x 1,..., x N), где х iобозначает совокупность пространственных координат (r i) и спиновой переменной (σ i) i-гo электрона. Тогда N-электронная матрица плотности ρ Nопределяется аналогично одноэлектронной (4.6):

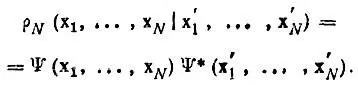(4.10)

Диагональные элементы матрицы плотности ρ Nхарактеризуют вероятность того, что первый электрон локализован в точке x 1, в то время как второй — в точке х 2, третий — в точке х 3и т д. Конечно, в силу неразличимости электронов их нумерация является произвольной.

Рассматриваемые N электронов могут входить в состав системы включающей также и другие частицы. Например, молекулы состоят из электронов и атомных ядер, образующих единую систему. Пусть состояние последней определяется нормированной функцией Φ(x 1,..., x N,ξ), причем ξ обозначает совокупность переменных всех частиц, не являющихся электронами (т. е. ядер). Состояние N-электронной системы в общем случае не может описываться Ψ-функцией и в этом смысле не является чистым [34] В так называемом адиабатическом приближении электронной системе в молекуле сопоставляется определенная Ψ-функция, которая зависит и от ядерных координат. . Но оно может характеризоваться N-частичной редуцированной матрицей плотности: