Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

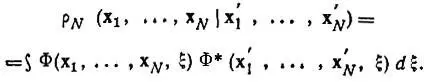(4.11)

Термин "редуцированная" в применении к матрице плотности означает, что некоторые переменные в левом и правом наборах ее аргументов отождествляются 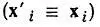и затем по ним проводится интегрирование.

Подобным образом определяются редуцированные матрицы плотности для k-электронных подсистем N-электронной системы:

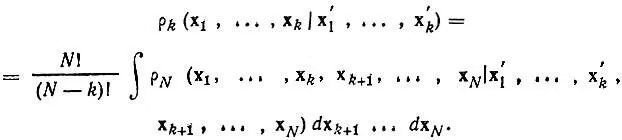(4.12)

Целесообразность введения множителя 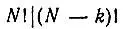обусловлена тождественностью электронов. В частности, редуцированная одноэлектронная матрица плотности определяется через N-электронную равенством

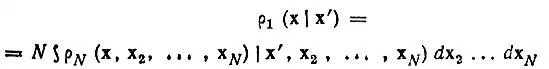(4.13)

и нормирована на число электронов N:

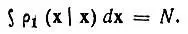(4.14)

Часто используют бесспиновую матрицу плотности

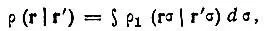(4.15)

где проведено интегрирование (или суммирование) по спиновой переменной σ.

Отметим теперь некоторые используемые в дальнейшем математические свойства редуцированных матриц плотности.

Вследствие антисимметричности N-электронной функции Ψ (или Φ) относительно перестановок электронных переменных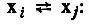

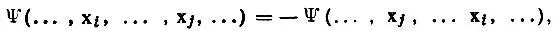(4.16)

k-частичные матрицы плотности при 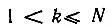антисимметричны в левой и правой группах аргументов, разделенных вертикальной чертой:

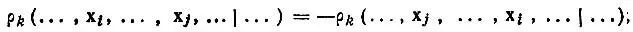(4.17a)

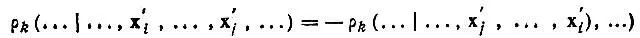(4.17б)

Из определения ρ kследует также, что

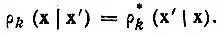(4.18)

Учитывая сказанное на с.102 об интегральном представлении операторов , мы можем утверждать, что матрица плотности является ядром некоторого эрмитового оператора k -частичной плотности вероятности ρ k :

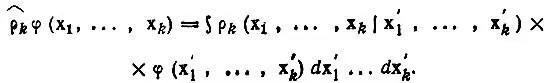
He следует думать, однако, что этот оператор соответствует некоторой наблюдаемой физической величине. Его роль в квантовой теории состоит в том, что он характеризует состояние N -электронной системы в той мере, в какой это необходимо для определения ожидаемого значения любой физической величины, представленной суммой k -электронных операторов. При этом последние не зависят от состояния рассматриваемой многоэлектронной системы. Среднее значение оператора 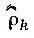для некоторого k -электронного состояния определяет заселенность этого состояния. Собственные функции 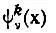оператора 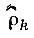называются функциями "естественных" k-частичных состояний, а собственные значения — естественными заселенностямиn (k) ν. Функции 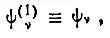определяющие одночастичные состояния с заселенностями 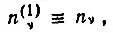называются естественными спин-орбиталямии удовлетворяют уравнению

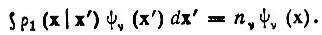(4.20)

Бесспиновые ψ ν (r), удовлетворяющие аналогичному уравнению на собственные значения матрицы плотности ρ (r|r')называются "естественными" орбиталями.

В качестве примера рассмотрим молекулу водорода Н 2. Естественные молекулярные орбитали для этой молекулы определяются исключительно из соображений симметрии (если их ищут в виде линейной комбинации двух атомных 1s-орбиталей) и классифицируются на симметричную ( g ) и антисимметричную ( u ) МО:

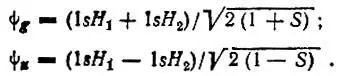
В то же время естественные заселенности связывающего (ψ g) и разрыхляющего (ψ u) одноэлектронных состояний зависят от способа построения полной двухэлектронной функции молекулы Н 2из одноэлектронных (табл. 3).

Таблица 3. Естественные заселенности в молекуле H 2 [35]

Матрицу плотности ρ (r|r'), как и матрицы плотности более высокого порядка, можно представить через "естественные" заселенности и соответствующие естественные функции в виде естественного разложения:

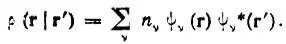(4.21)

Такое представление матрицы плотности обобщает приведенное выше выражение (4.6) для одноэлектронной матрицы плотности "чистого" состояния одного электрона с определенной ψ-функцией. В случае многоэлектронной системы отдельному электрону уже нельзя сопоставить какую-либо функцию ψ( r). Состояние электрона в многоэлектронной системе является "смешанным" и описывается одноэлектронной матрицей плотности ρ( r|r') или наборомфункций ψ ν( r) и соответствующих им "чистых" состояний. При этом вероятность пребывания электрона в состоянии, определяемом функцией ψ ν, характеризуется естественной заселенностью n ν.