Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи
- Название:Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:1980
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи краткое содержание
Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
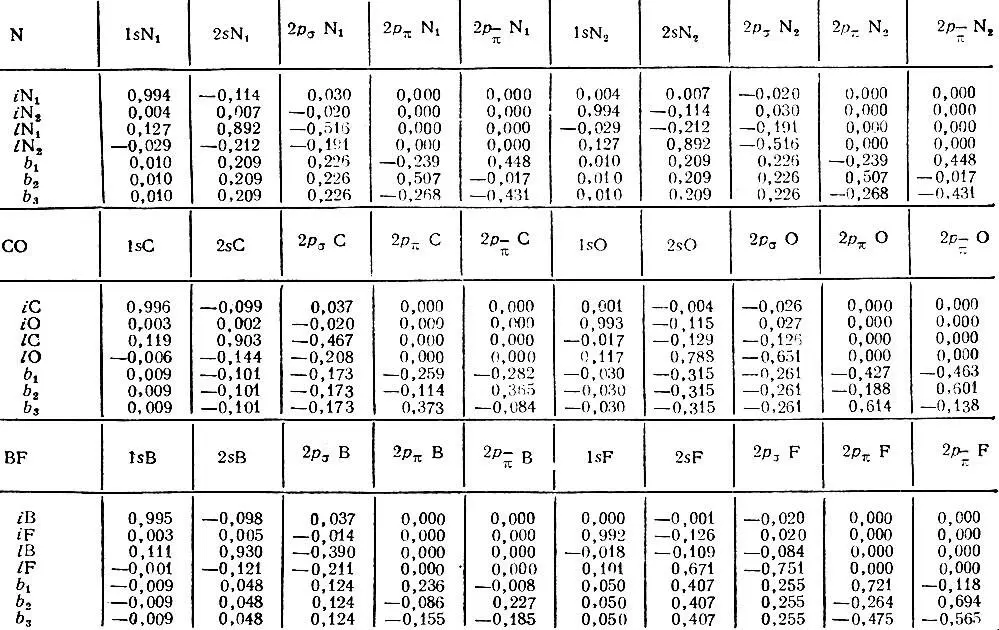
Таблица 5. Орбитали Эдмистона-Рюденберга в молекулах N 2 , CO и BF
Практическая реализация метода Эдмистона-Рюденберга предполагает использование формализма самосогласованного поля и вычисление большого числа двухэлектронных интегралов, что представляет довольно сложную математическую задачу. Количество таких интегралов, как и время, необходимое для максимизации J (1)(или минимизации J (2)и К), очень быстро растет с увеличением числа электронов в системе и числа базисных АО, используемых для представления МО.
Следует отметить также, что метод Эдмистона и Рюденберга, строго говоря, не гарантирует соответствия между локализованными МО и отдельными атомами или связями. Впрочем, это обстоятельство может рассматриваться не только как недостаток, но и как достоинство метода, поскольку он допускает в принципе представление МО в базисе, существенно отличающемся от многоцентрового базиса АО.
В вычислительном отношении более удобным, чем метод Эдмистона-Рюденберга, является метод Бойса [31]. В качестве критерия, определяющего степень локализации МО, в этом методе используется сумма квадратов расстояний ( R i ) между центрами тяжести орбиталей:
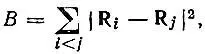 (4.34)
(4.34)
где
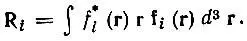 (4.35)
(4.35)
Локализованные по Бойсу МО характеризуются максимальным разделением в пространстве по критерию В и одновременно минимальными среднеквадратическими радиусами, точнее минимальным значением суммы их квадратов:
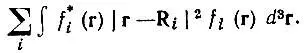 (4.36)
(4.36)
Недостатком метода Бойса является то, что он не обеспечивает эффективного разделения валентных и остовных АО. Например, 1s- и 2s-орбитали сферически-симметричны и никаким преобразованием нельзя изменить расстояния между их центрами тяжести (которое всегда равно нулю). С другой стороны, смешение остовной 1s-орбитали с валентными np-орбиталями должно приводить к увеличению расстояния от нулевого до некоторого конечного (для гибридных АО) значения. Максимуму значения В при этом должна соответствовать тетраэдрическая гибридизация 1s- и nр-АО. В действительности наряду с остовной 1s-орбиталью следует принимать во внимание и валентную ns-AO. Именно она должна смешиваться с другими валентными АО. Но с учетом сказанного выше ясно, что метод Бойса может приводить к завышенному вкладу остовных АО в связывающие МО.
Метод проецирования.Метод проецирования, предложенный в работах Полака [73] и позднее развитый Роби [74], основан на том, что одноэлектронная матрица плотности ρ 1( x|x') в однодетерминантном приближении является ядром оператора проектирования на подпространство занятых молекулярных спин-орбиталей. Поэтому для любой нормированной спин-орбитали ψ проекционная норма
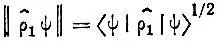 (4.37)
(4.37)
удовлетворяет неравенству
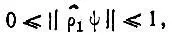 (4.38)
(4.38)
причем 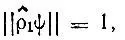 если спин-орбиталь ψ целиком принадлежит подпространству занятых молекулярных спин-орбиталей, и
если спин-орбиталь ψ целиком принадлежит подпространству занятых молекулярных спин-орбиталей, и 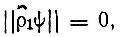 если спин-орбиталь ψ ортогональна к этому подпространству.
если спин-орбиталь ψ ортогональна к этому подпространству.
Следуя Полаку, локализованную на атоме А МО, описывающую неподеленную электронную пару или орбиталь внутренней оболочки атома, можно определять как линейную комбинацию орбиталей атома А (т. е. как гибридную АО этого атома):
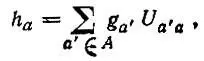 (4.39)
(4.39)
максимизирующую проекционную норму 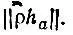 . Если бесспиновая одноэлектронная матрица плотности ρ( r|r') представлена в базисе АО g матрицей
. Если бесспиновая одноэлектронная матрица плотности ρ( r|r') представлена в базисе АО g матрицей
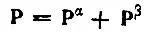 (4.40)
(4.40)
и базис g характеризуется матрицей перекрывания S, причем S' a= 0 для а, а' ∈ А, то столбец U a, представляющий искомую гибридную АО h a, является собственным вектором матрицы Q (A)образуемой матричными элементами (SPS) aa' ∈ А, и этот собственный вектор отвечает максимальному собственному значению n а. Когда последнее равно двум, гибридная АО h aбудет в точности совпадать с естественной МО, описывающей неподеленную электронную пару; когда n a≈ 2, гибридная АО h aбудет аппроксимировать такую орбиталь.
Двух-, трех- ... и K-центровые МО, локализованные на атомных группах (связях) G = (A 1,..., A K) и представленные линейными комбинациями вида
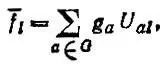 (4.41)
(4.41)
определяются в методе проецирования аналогичным образом, т. е. посредством диагонализации матриц Q (G)при условии ортонормированности
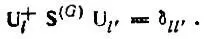 (4.42)
(4.42)
Согласно работам [73, 74], процедура локализации МО осуществляется в следующей последовательности:
1) сначала определяются одноцентровые 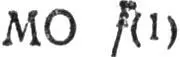 , локализованные на остовных и валентных оболочках отдельных атомов;
, локализованные на остовных и валентных оболочках отдельных атомов;
2) одноцентровые 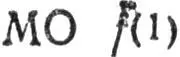 исключаются из исходного базиса преобразованием
исключаются из исходного базиса преобразованием
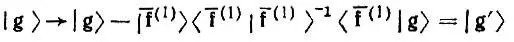 (4.43)
(4.43)
и канонической ортонормировкой линейно-зависимого набора орбиталей g';
3) в полученном ортонормированием базисе, включающем меньшее число орбиталей, чем исходный базис АО g, определяются двухцентровые МО 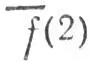 ;
;
Интервал:
Закладка:









