Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

соответствует виртуальная разрыхляющая

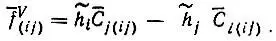(4.52)

Остальные локализованные виртуальные МО являются просто вакантными гибридными АО.

Если исходный набор МО

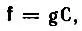(4.53)

включающий и виртуальные МО, преобразуется в набор 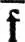строго локализованных МО (также включающий виртуальные МО) преобразованием

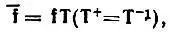(4.54)

то матрица Т, осуществляющая строгую локализацию исходных МО f, определяется как

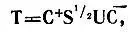(4.55)

где

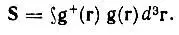
В рассматриваемом примере (HCN) гибридные АО выражаются через исходные сферические АО согласно следующим равенствам:

Из этих выражений видно, что в приближении строгой локализации МО гибридные АО h 1C и h 1N являются орбиталями электронных пар остова, h 3N-ГAO представляет неподеленную электронную пару азота, остальные ГАО образуют МО σ-типа, локализованные на связях НС и CN. Степень локализации МО характеризуется среднеквадратическим отклонением матрицы плотности Р hот эталонной :

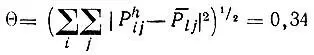(4.56)

и удвоенной суммой квадратов интегралов перекрывания строго локализованных 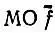с исходными f:

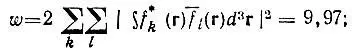(4.57)

ω не может превосходить числа электронов N (в рассматриваемой системе ω< 10), и локализация будет тем точнее, чем ближе значения ω и N.

Метод эталонной матрицы плотности обобщается для случаев, когда необходимо учитывать полярность локализованных двухцентровых МО. Такое обобщение можно осуществить при замене в эталонной матрице плотности блоков

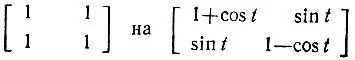
и при определении параметров поляризации t вариационным методом [63]. Строго ковалентным связывающим МО при этом будет соответствовать значение t = π/ 2, а неподеленным электронным парам и вакантным ГАО — t = 0 или π. Строго говоря, такое обобщение рассматриваемого метода уже не позволяет называть его методом эталонной матрицы плотности. Легко убедиться, однако, что учет полярности связей, как правило, возможен и с фиксированной эталонной матрицей , т. е. результаты ее вариационного определения могут быть предсказаны заранее. При этом для ГАО неподеленных электронных пар (h l) ll= 2, Для вакантных ГАО (h i) ii= 0, а для валентных ГАО h aи h b, образующих локализованную 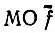ab, эталонные заселенности aa, 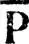bbи порядки связей 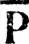abопределяются равенствами

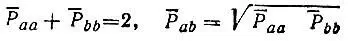
и условием инвариантности атомных зарядов относительно гибридизации АО.

Коэффициенты разложения строго локализованных МО по ортогонализованным ГАО выражаются через их заселенности по формулам

Для молекулы HCN заселенность 1s-орбитали водорода равна 0,855 и, следовательно, заселенность гибридной АО углерода h 2C равна 1,145. Так как сумма заселенностей всех σ-орбиталей углерода составляет 4,099, заселенность его h 3С-ГАО равна 0,954. Определяя теперь порядки связей (недиагональные элементы матрицы Р) как среднегеометрические значения соответствующих заселенностей (диагональных элементов матрицы ), получаем

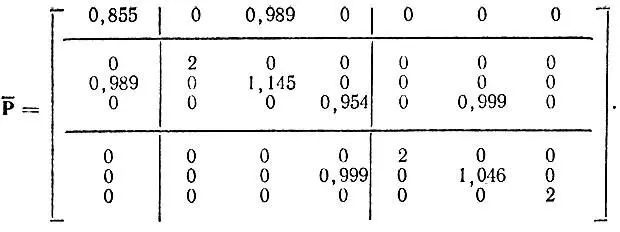
Вычисления свидетельствуют, что при учете полярности локализованных МО матрица Р hостается практически неизменной. Коэффициенты гибридизации также почти не меняются. В то же время максимум ω повышается до 9,98 (w ≈ 10), а минимум θ понижается до 0,25. Таким образом, учет полярности локализованных МО заметно улучшает аппроксимацию "точной" матрицы плотности Р hэталонной матрицей , хотя и является несущественным для определения характера гибридизации АО.

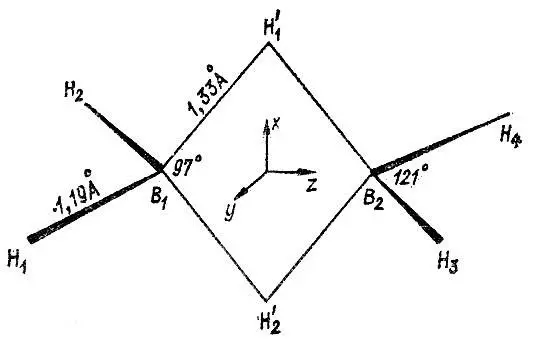
Метод эталонной матрицы плотности допускает обобщение на системы с многоцентровыми связями [22]. Типичным примером химического соединения ОМ, которого нельзя локализовать исключительно в одноцентровые и двухцентровые МО, является молекула диборана В 2Н 6(рис. 19). Два из шести атомов водорода в этой молекуле имеют по два равноотстоящих соседних атома (B 1и В 2). Каждый из атомов бора, в свою очередь, связан с четырьмя атомами водорода. Следует учитывать также возможность непосредственного химического взаимодействия атомов бора друг с другом.