Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

атомов. Однако анализ заселенностей осложняется перекрыванием атомных орбиталей в молекуле.

Если последние ортогональны, т. е. не перекрываются, то их заселенности определяются однозначно. При этом заселенность па имеет смысл вероятности нахождения электрона в состоянии, заданном атомной орбиталью φ а, и может быть выражена как математическое ожидание:

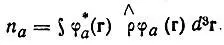(4.58)

Если атомные орбитали неортогональны, то положение осложняется. Понятие заселенности отдельной АО становится неоднозначным и распадается на дополняющие друг друга понятия полной, неподеленной и аддитивной заселенности и заселенности перекрывания, которые связаны с различными способами ортонормировки атомно-орбитального базиса {φ}.

Полные заселенности(n + а) орбиталей φ анеортогонального базиса {φ} определяются аналогично заселенностям ортогонального базиса:

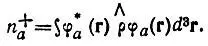(4.59)

Предполагая, что оператор электронной плотности ρ представлен в базисе {φ} матрицей 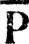, определение (4.59) можно переписать также в виде

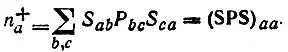(4.60)

Детальное исследование заселенностей n + aбыло проведено Дэвидсоном [37] и Роби [74], которые показали, в частности, что

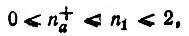
где n 1— наибольшая из естественных заселенностей. Это неравенство, как и аналогичные неравенства для определяемых ниже заселенностей n - aи n 0 а, следует из условия антисимметрии многоэлектронной функции Ψ(х 1,..., х N) относительно перестановок электронных координат.

Неподеленную заселенность(n - а) орбитали φ аможно определить как заселенность ее компоненты, которая ортогональна ко всем прочим орбиталям φ:

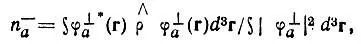(4.62)

где

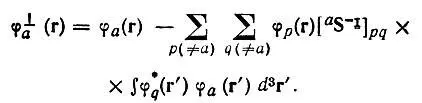(4.63)

aS в формуле (4.63) обозначает матрицу перекрывания, полученную из полной матрицы S вычеркиванием интегралов перекрывания S ab, включающих рассматриваемую орбиталь φ а.Такая ортогонализация (аналогичная ортогонализации по методу Шмидта) исключает из полной заселенности n + ату ее часть, которая принадлежит не только φ а, но и остальным орбиталям неортогонального базиса (рис. 23).

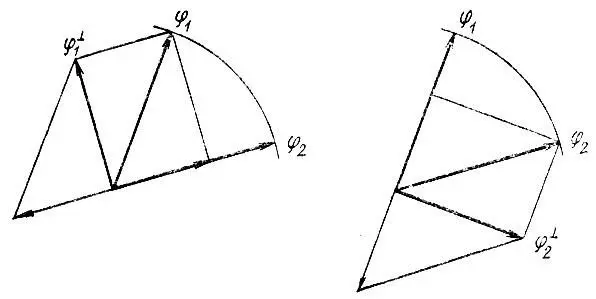
Рис. 23. Геометрическая иллюстрация к определению неподеленной электронной заселенности

Учитывая отмеченное Галлупом и Норбеком [40] равенство

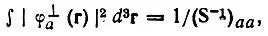(4.64)

выражение(4.62) можно привести к чрезвычайно простому виду

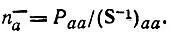(4.65)

В частном случае одноэлектронной системы, состояние которой описывается орбиталью

(4.66)

диагональные элементы матрицы плотности равны

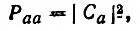(4.67)

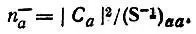(4.68)

Эта формула, то чиее ее правая часть, приводилась в работе [40], но лишь в качестве промежуточного результата. Окончательное выражение для заселенностей (по Галлупу и Норбеку) получалось путем нормирования n - ана единицу:

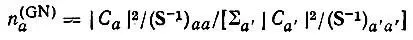(4.69)

Обобщение формулы (4.69) на многоэлектронные системы, очевидно, должно осуществляться заменой |С а| 2на Р аа:

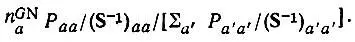(4.70)

Однако такой подход к проблеме является ошибочным. Расчеты свидетельствуют, в частности, о чрезмерно больших значениях n(GN) для АО внутренних оболочек и неподеленных электронных пар. Например, в молекуле LiH:

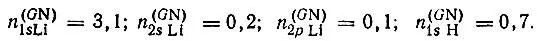
Заселенность перекрыванияорбитали φ ас остальными орбиталями неортогонального базиса φ определяется как разность между полной и неподеленной заселенностями:

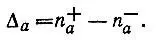(4.71)

Заселенность перекрывания 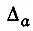представляет ту долю полной электронной заселенности, которая принадлежит одновременно к рассматриваемой и всем прочим базисным АО. Нетрудно убедиться в том, что величина 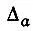равна нулю, если АО φ ане перекрывается ни с одной из орбиталей базиса φ, т. е. если

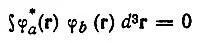(4.72)

для всех b≠a.

Аддитивная заселенность.

Сумма засел енностей n + aили n - апо всем базисным орбиталям совпадает с числом электронов (N) в рассматриваемой системе только в том случае, если эти орбитали ортогональны. Иными словами, заселенности орбиталей неортогонального базиса неаддитивны.

Чтобы определить аддитивные заселенности АО, необходимые, например, для вычисления формальных зарядов атомов, следует сопоставить каждой АО φ анеортогонального базиса орбиталь φ λ aнекоторого ортонормированного базиса. Требование минимальной деформации исходных орбиталей в процессе ортогонализации однозначно отбирает из всех возможных методов ортогонализации "симметричный" метод Лёвдина (рис. 24)

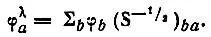(4.73)